【Python】線形回帰とは何か?
線形回帰は、データ分析や機械学習の入門として最もよく使われる手法の一つです。
シンプルながら強力なこの方法を理解すれば、データからパターンを見つけて予測ができるようになります。
この記事では、線形回帰の基本から実際のPythonでの実装まで説明していきます。
線形回帰とは?
線形回帰とは、データポイント間の関係を直線で表現する方法です。
たとえば、勉強時間と成績の関係や、広告費と売上の関係などを分析するのに使われます。
簡単に言うと、点と点の間に「最も当てはまりの良い直線」を引くことです。
どうして「線形」回帰というの?
「線形」という言葉は「直線的な」という意味です。
つまり、入力値(説明変数)と出力値(目的変数)の間に直線関係があると仮定しています。
数学的には以下のような式で表されます:
y = mx + b
ここで:
- y は予測したい値(例:テストの得点)
- x は入力値(例:勉強時間)
- m は傾き(勉強時間が1時間増えると得点がm点上がる)
- b は切片(勉強時間が0のときの得点)
線形回帰の仕組み
線形回帰の目標は、実際のデータポイントと予測値の差(誤差)が最小になるような直線を見つけることです。
この「最適な直線」を見つける方法として、「最小二乗法」という手法がよく使われます。
これは、すべての誤差を二乗して合計した値が最小になる直線を探す方法です。
Pythonで線形回帰を実装してみよう
それでは実際にPythonで線形回帰を試してみましょう。
scikit-learnというライブラリを使うと簡単に実装できます。
まずは必要なライブラリをインポートします:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
import pandas as pd
# データの準備
# 勉強時間(時間)
study_hours = np.array([1, 2, 3, 4, 5, 6, 7, 8]).reshape(-1, 1)
# テストの点数
test_scores = np.array([60, 65, 75, 70, 80, 85, 90, 95])
# 散布図をプロット
plt.scatter(study_hours, test_scores)
plt.title("Study Hours vs Test Scores")
plt.xlabel("Study Hours")
plt.ylabel("Test Scores")
plt.grid(True)
plt.show()
# 線形回帰モデルの作成
model = LinearRegression()
model.fit(study_hours, test_scores)
# 傾きと切片の確認
print(f"傾き(係数): {model.coef_[0]}")
print(f"切片: {model.intercept_}")
# 予測線の追加
prediction_x = np.array([0, 10]).reshape(-1, 1)
prediction_y = model.predict(prediction_x)
plt.scatter(study_hours, test_scores)
plt.plot(prediction_x, prediction_y, color='red', linewidth=2)
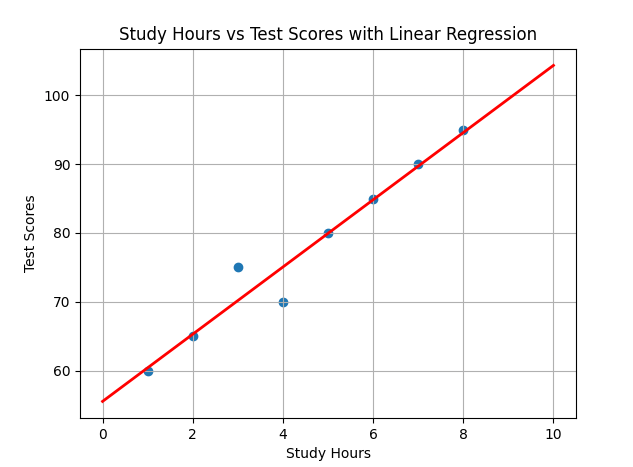
plt.title("Study Hours vs Test Scores with Linear Regression")
plt.xlabel("Study Hours")
plt.ylabel("Test Scores")
plt.grid(True)
plt.show()
# 新しいデータで予測
new_hours = np.array([3.5, 9]).reshape(-1, 1)
predicted_scores = model.predict(new_hours)
print(f"3.5時間勉強した場合の予測点数: {predicted_scores[0]}")
print(f"9時間勉強した場合の予測点数: {predicted_scores[1]}")
このコードを実行すると、勉強時間とテスト点数の関係を表す散布図と、その関係を表す最適な直線が描画されます。
線形回帰の評価方法
モデルがどれだけ良いかを評価するために、いくつかの指標を使います:
- 決定係数(R²) - モデルがデータをどれだけ説明できているかを0〜1の値で表します。
1に近いほど良いモデルです。
- 平均二乗誤差(MSE) - 予測値と実際の値の差の二乗の平均です。小さいほど良いモデルです。
これらの評価指標をPythonで計算してみましょう。
上記のコードのあとに、以下のコードを加えます。
from sklearn.metrics import r2_score, mean_squared_error
# R²スコア
r2 = r2_score(test_scores, model.predict(study_hours))
print(f"決定係数(R²): {r2}")
# 平均二乗誤差
mse = mean_squared_error(test_scores, model.predict(study_hours))
print(f"平均二乗誤差(MSE): {mse}")
線形回帰のメリットとデメリット
線形回帰には以下のようなメリットとデメリットがあります:
| メリット | デメリット |
|---|---|
| 理解しやすい | 非線形の関係を表現できない |
| 実装が簡単 | 外れ値に弱い |
| 計算が速い | 複雑なパターンには適さない |
| 解釈がしやすい | 変数間の関係が複雑な場合に不向き |
多変量線形回帰
ここまでは一つの説明変数(勉強時間)から一つの目的変数(テスト点数)を予測する単回帰について説明しました。
しかし実際には、複数の要因が結果に影響することが多いです。
例えば、テスト点数は勉強時間だけでなく、睡眠時間や前回のテスト点数なども関係するかもしれません。
このように複数の説明変数を使う線形回帰を「多変量線形回帰」と呼びます。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 多変量線形回帰の例
# 勉強時間、睡眠時間、前回のテスト点数
X_multi = np.array([
[2, 7, 65], # 学生1: 勉強2時間、睡眠7時間、前回65点
[3, 8, 70], # 学生2
[4, 6, 75], # 学生3
[5, 7, 80], # 学生4
[6, 8, 85], # 学生5
])
# 今回のテスト点数
y_multi = np.array([70, 75, 80, 85, 90])
# 多変量線形回帰モデルの作成
multi_model = LinearRegression()
multi_model.fit(X_multi, y_multi)
# 係数と切片の確認
print(f"係数: {multi_model.coef_}")
print(f"切片: {multi_model.intercept_}")
# 新しいデータで予測
new_student = np.array([[4, 7, 75]]) # 勉強4時間、睡眠7時間、前回75点
prediction = multi_model.predict(new_student)
print(f"新しい学生の予測点数: {prediction[0]}")
実際の応用例
線形回帰は様々な分野で使われています:
- 経済・金融 - 価格予測、株価分析
- 医療 - 患者の回復時間の予測
- マーケティング - 広告効果の分析
- 不動産 - 住宅価格の予測
まとめ
線形回帰は、データの関係を直線で表現するシンプルながら強力な手法です。
Pythonを使えば、数行のコードで実装できます。
また、理解しやすく解釈もしやすいため、データ分析の入門として最適。
しかしすべての関係が線形とは限らないので、データの性質をよく理解した上で使うことが大切です。
Discussion