オープンデータを酷使して理想の道を探す
この記事はFOSS4G Advent Calendar 2024 の25日目の記事です
概要
この記事ではオープンデータから理想の道路を探すための方法について解説します。
この記事のゴールは指定した緯度経度の範囲内から理想の道を抽出し上位10件をLeaflet.jsとthree.jsに表示する所までとします。
理想の道は「イニシャルDで走るような峠道」としました。
 イニシャルDで走るような峠道
イニシャルDで走るような峠道
最終イメージはこんな感じです。
| 上位10件を表示(Leaflet.js) | 峠を3Dで表示(three.js) |
|---|---|
 |
 |
内容は去年の私が書いたこれをブラシアップしたものになっています。
使用するデータ
探索ロジックで使用するデータはOpenStreetMapの地図データを主軸として、その上に別のデータを重ね合わせて情報を増やした物を使用します。
こちらが使用したデータです。
- OpenStreetMapの道路ネットワーク
- OpenStreetMapのタグ(トンネル, 橋等)
- 国土地理院の標高モデル
- 国土地理院の衛星写真
- OvertureMapsの建物ポリゴン
- 県単位のポリゴン
探索する道路の特徴
今回の対象の道は「イニシャルDで走るような峠道」です。
どのような道かと言うと周囲を気にせずに運転が楽しめてハンドル操作が激しい道です。
このような道路の特徴を大きく分けると「走りやすい道」と「三次元的に複雑な道」にわけられます。
走りやすい道
走りやすい道とは周辺に意識を向けることなく自分の運転にのみ集中できる道の事です。
もう少し具体的にすると、道幅が広くドライバーが対向車や前後の車を意識する事なく走行できて民家や交差点が少ないような道を指します。
道幅が狭い道は常に対向車を意識する必要があったり、民家や交差点が多ければ歩行者や周囲の視線に意識が向いてしまうので運転に集中する事ができません。
走りやすい道にはこのような特徴を持っています。
- 交通量が少ない
- 交差点が少ない
- 周辺に民家が少ない
- 道幅がある程度確保されている

走りやすい道のイメージ
三次元的に複雑な道
峠道はx, y, z軸方向に複雑な形状をしています。このような道は車の特性が現れやすいです。車体のボディ剛性やタイヤ剛性が高ければ車はクイックに曲がりますし、トルクがあればコーナーの立ち上がりで加速感を感じる事ができます。

3次元的に複雑な道のイメージ
x, y軸の複雑性はOpenStreetMapの平面的な道路形状から求める事ができ、z軸は国土地理院の標高モデルから求める事ができます。
3次元的に複雑な道はこのような特徴を持っています。
- 勾配がついている道
- 波打つような坂が多い道
- 複雑なステアリング操作を要求される道
処理の流れ
オープンデータから峠を抽出してLeaflet.jsに表示するまでのフローはこのようになっています。

峠の候補になる道路区間を取得
まず峠の候補になる区間(LineString)の一覧を取得します。この区間が後続で行う評価ロジックの対象になります。これはOpenStreetMapの道路ネットワークから作成します。
道路ネットワークに対して峠の特徴を持つ可能性のある道路区分で絞り込みをかけて残ったネットワークのノードの間が峠の候補となります。
# 指定ポリゴン内の道路ネットワークを取得する
def fetch_graph(
search_area_polygon : MultiPolygon,
) -> nx.Graph:
ox.settings.useful_tags_way += ["yh:WIDTH"] + ["source"] + ["tunnel"] + ["bridge"]
graph = ox.graph_from_polygon(
search_area_polygon,
network_type="drive",
simplify=True,
retain_all=True,
# 道路区分で抽出
custom_filter='["highway"~"secondary|secondary_link|primary|primary_link|trunk|trunk_link|tertiary"]["lanes"!=1]',
)
return graph
| 道路区分で絞り込んだもの | 峠の候補 |
|---|---|
 このノードとノードの間が峠の候補の区間 このノードとノードの間が峠の候補の区間
|
 ノード間のLineStringの一覧。これが峠の候補。 ノード間のLineStringの一覧。これが峠の候補。
|
交差点が多い道を弾く
交差点が多いという事は脇道からの飛び出しや歩行者に意識が持っていかれてします。このような道は運転に集中できません。
さきほどの「峠の候補になる区間」で取得した道には交差点の情報を持っていないのでLineString内の全ポイントと重なる道路を探す事で交差点の数を求める事ができます。
def generate(gdf: GeoDataFrame, search_area_polygon) -> Series:
# 全道路を取得
graph = ox.graph_from_polygon(
search_area_polygon,
network_type="drive",
simplify=True,
retain_all=True,
)
all_nodes = ox.graph_to_gdfs(graph, nodes=True, edges=False)
sindex_nodes = all_nodes.sindex
# 分岐数を取得
def func(row):
sindex_matche_indexs = list(sindex_nodes.intersection(row.geometry.bounds))
sindex_matche_nodes = all_nodes.iloc[sindex_matche_indexs]y内のノードから絞り込むのでめっちゃはやい。
matche_nodes = sindex_matche_nodes[sindex_matche_nodes.intersects(row.geometry)]
result = matche_nodes["street_count"].sum() - (len(matche_nodes) * 2)
return result
tqdm.pandas()
series = gdf.progress_apply(func, axis=1)
return series
周辺に建物が多い道を弾く
周辺に建物が多いという事は人間が住んでいる可能性があり、人間の飛び出しや視線に意識が持っていかれてしまいます。そういう道は気分が悪いので弾きます。
弾くための方法としては、OverTrueMapから建物ポリゴンを取得して候補区間の周辺の建物の数を計算します。
建物ポリゴンはOpenStreetMapにも含まれていますがOverTrueMapは内部にOpenStreetMapとMicrosoftの機械学習で作られた建物ポリゴンが混在しているのでデータ数が多いこっちを使ったほうがよいです。
OverTrueMapsの建物ポリゴンはこちらからDLできます。DLした物をローカルのPostGISに挿入してpythonから扱いやすいような形に調整しておきます。
具体的な計算方法は、候補区間の道路から垂直に15mの法線を伸ばしてその中に含まれる建物ポリゴン数を計算し、それを周辺の建物の数としました。
このような感じで候補区間周辺の建物ポリゴンを判別します。

def main(line: LineString):
bbox = line.bounds
# LinStringから上下に15m垂直に伸ばしたポリゴンを作成する。
polygon = create_vertical_polygon(line.coords, 15)
# LineStirngのバウンディングボックス内の建物を取得
buildings = get_nearby_builgings(bbox[0], bbox[1], bbox[2], bbox[3])
# ポリゴン内の建物を取得
match_buildings = []
for index, building in enumerate(buildings):
if building.intersects(polygon):
match_buildings.append(building)
unique_buildings = list(dict.fromkeys(match_buildings))
# 表示
fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(*line.xy, color="blue", label="LineString")
x, y = polygon.exterior.xy
ax.fill(x, y, color="cyan", alpha=0.3, label="Polygon (Buffer)")
label_added = False
for building in unique_buildings:
if building.geom_type == "Polygon": # 建物がPolygonの場合
x, y = building.exterior.xy
ax.fill(x, y, color="red", alpha=0.5, label="Building (Polygon)" if not label_added else "")
label_added = True
ax.set_title("LineString, Polygon, and Buildings")
ax.set_xlabel("Longitude")
ax.set_ylabel("Latitude")
ax.legend()
plt.show()
# 近くの建物を取得する
def get_nearby_builgings(min_longitude, min_latitude, max_longitude, max_latitude):
session = get_db_session()
try:
buildings = []
# SQLクエリを実行
query = text(f"""
SELECT ST_AsText(geometry) as geometry
FROM buildings
WHERE ST_Intersects(
geometry,
ST_MakeEnvelope(:min_longitude, :min_latitude, :max_longitude, :max_latitude, :srid)
);
""")
result = session.execute(query, {
'min_longitude': min_longitude,
'min_latitude': min_latitude,
'max_longitude': max_longitude,
'max_latitude': max_latitude,
'srid': 4326
})
result = result.fetchall()
for data in result:
geometry = wkt.loads(data[0])
buildings.append(geometry)
finally:
session.close()
return buildings
line =[[35.6654192,138.6443673],[35.6654624,138.6443208],[35.6655902,138.6441203],[35.6656294,138.6439655]]
coordinates = [(lon, lat) for lat, lon in line]
main(LineString(coordinates))
交通量が多い道を弾く
交通量が多い道は前後の車に意識が持っていかれてしまい運転に集中できません。
これについてはロジックを組む必要はありません。
これまでの処理の「周辺に建物が多い道を弾く」、「交差点が多い道を弾く」とこの先に行う「3次元的に複雑な道」で絞り込みを行うとその道は交通量が少ない道となります。
峠道は基本交通量が少ないので計算をしなくてもそれ以外の要素で絞り込むと結果的に交通量が少なくなりました。
車幅がある程度確保されている道を評価
車幅がある程度確保されてる道は対向車を気にする必要がありません。逆に車幅が狭く2台の車が同時に通れないような道は常に対向車に意識を集中させる必要があり運転に集中できません。
峠においてこの車幅は重要なパラメーターでこの判別ができないと酷道が引っかかってしまいます。

酷道
別の記事でも書きましたがオープンデータから道幅を正確に判別する事は難しいので自前で作った車線数データから車幅を計算します。
| 自前で作った車線データ | ←をズームしたもの |
|---|---|
 青: 2車線, オレンジ: 1.5車線, 赤: 1車線 青: 2車線, オレンジ: 1.5車線, 赤: 1車線
|
 |
車幅の計算方法は候補区間内の座標と一致する車線データを取得し、そのデータ数と車線数の平均から計算しました。
def main(line: LineString):
coords = list(line.coords)
# LineStringのバウンディングボックスを取得
min_longitude, min_latitude, max_longitude, max_latitude = line.bounds
srid = 4326
session = get_db_session()
# バウンディングボックス内のデータを取得
result = session.execute(text(f"SELECT ST_X(point) AS longitude, ST_Y(point) AS latitude, road_width_type FROM locations WHERE ST_Intersects(ST_MakeEnvelope({min_longitude}, {min_latitude}, {max_longitude}, {max_latitude}, {srid}), locations.point)"))
result = result.fetchall()
# LineStringと一致するデータのみ取り出す
match_width_data = []
for coord in coords:
for data in result:
if data.longitude == coord[0] and data.latitude == coord[1]:
match_width_data.append(data._asdict())
# 一致した車線データを元にスコアを計算(1に近いほど2車線に近い
# 2車線(TWO_LANE) = 1
# 1.5車線(ONE_LANE_SPACIOUS) = 0.5
# 1車線(ONE_LANE) = 0.01
score = 0
for width_data in match_width_data:
if width_data['road_width_type'] == "TWO_LANE" or width_data['road_width_type'] == "TWO_LANE_SHOULDER":
score += 1
elif width_data['road_width_type'] == "ONE_LANE_SPACIOUS":
score += 0.5
elif width_data['road_width_type'] == "ONE_LANE":
score += 0.01
# スコアを表示
print(score/len(match_width_data))
line =[[35.6654192,138.6443673],[35.6654624,138.6443208],[35.6655902,138.6441203],[35.6656294,138.6439655]]
coordinates = [(lon, lat) for lat, lon in line]
main(LineString(coordinates))
道路の標高値を計算する
国土地理院から日本国土の標高モデルが公開されていますがこのモデルは地球表面の標高値です。
以下はドキュメントから抜粋
地表面の測定値に基づいているため、構造物(建物、高架橋等)の高さを反映し
たものではありません。
今回必要な標高値は地球面の標高値ではなく道路の標高値です。
そのため地球面の標高値から補正をかけ道路の標高値を計算する必要があります。
こちらは補正をかけずに道路区間内の各座標から国土地理院の標高モデルの標高値を取得してthree.jsに描画したものです。
道路の形状になっていませんね。

りんごの皮みたいな形状をしてます。
補正をかける必要があるのは3つです。
- トンネル区間の補正
- 橋区間の補正
- 国の道路傾斜の基準にあわせた補正
トンネル区間の補正
OpenStreetMapにはトンネルの開始地点と終了地点の座標を持っています。この間の標高値が線形になるように補正をかけます。
class InfraType(Enum):
TUNNEL = 1
BRIDGE = 2
# トンネルと橋の標高値を調整する
# gdf = 補正するLineStringと標高値を含むGeoDataFrame
# infra_edges = 橋とトンネルの区間情報を含むGeoDataFrame
# infraType = 橋 or トンネル
def generate(gdf: GeoDataFrame, infra_edges: GeoDataFrame, infraType: InfraType) -> Series:
# トンネルの空間インデックスを作成
infra_edges_sindex = infra_edges["geometry"].sindex
def func(row: GeoSeries):
# row['bridge']とrow['tunnel']は配列と文字列の2パターンあり。
if (
infraType == InfraType.BRIDGE
and not any(x in row['bridge'] for x in ['yes', 'aqueduct', 'boardwalk', 'cantilever', 'covered', 'low_water_crossing', 'movable', 'trestle', 'viaduct'])
):
return row['elevation']
if(
infraType == InfraType.TUNNEL
and not any(x in row['tunnel'] for x in ['yes', 'building_passage', 'avalanche_protector', 'culvert', 'canal', 'flooded'])
):
return row['elevation']
base_edge_coords = list(row.geometry.coords)
# 1. 対象のエッジのバウンディングボックス内のトンネルのインデックスを取得(バウンディングボックスでの抽出なのでエッジ外のトンネルも含まれる可能性がある)
infra_edge_in_bbox_index_list = list(infra_edges_sindex.intersection(row.geometry.bounds))
# 2. インデックスからトンネルのエッジを取得
infra_edges_in_bbox = infra_edges.iloc[infra_edge_in_bbox_index_list]
# 3. 対象のエッジと重なるインフラのみを抽出(一旦座標が2以上重なっているかで判断)
target_infra_index_list = []
for idx, infra_edge in infra_edges_in_bbox.iterrows():
num_match_coords = sum([1 for coord in infra_edge.geometry.coords if coord in base_edge_coords])
if num_match_coords >= 2:
target_infra_index_list.append(idx)
if len(target_infra_index_list) == 0:
return row['elevation']
target_infra_edges = infra_edges_in_bbox.loc[target_infra_index_list]
# 始点と終点が線形になるように標高を調整
elevation_adjusted = row.elevation.copy()
for i, infra_edge in target_infra_edges.iterrows():
infra_coords = list(infra_edge.geometry.coords)
road_coords = list(row.geometry.coords)
nearest_outside_start = get_nearest_outside_point(road_coords, infra_coords[0], infra_coords)
nearest_outside_end = get_nearest_outside_point(road_coords, infra_coords[-1], infra_coords)
a_idx = base_edge_coords.index(nearest_outside_start)
b_idx = base_edge_coords.index(nearest_outside_end)
start_idx = min(a_idx, b_idx)
end_idx = max(a_idx, b_idx)
def linear_interpolation(arr, start_idx, end_idx) -> List[int]:
start_value = arr[start_idx]
end_value = arr[end_idx]
num_points = end_idx - start_idx + 1
interpolated_values = np.linspace(start_value, end_value, num_points)
interpolated_values_list = list(interpolated_values)
for i, value in enumerate(interpolated_values_list):
arr[start_idx + i] = value
return arr
elevation_adjusted = linear_interpolation(elevation_adjusted, start_idx, end_idx)
return elevation_adjusted
results = gdf.apply(func, axis=1)
return results
# トンネル外で最も近い座標を取得
def get_nearest_outside_point(road_coords: list, point: Tuple[float, float] , infra_coords: list):
if road_coords == infra_coords:
return min(road_coords, key=lambda x: Point(x).distance(Point(point)))
road_coords_without_infras = []
infra_coords_without_first_and_last = infra_coords[1:-1]
if not len(infra_coords_without_first_and_last) == 0:
road_coords_without_infras += [coord for coord in road_coords if not coord in infra_coords_without_first_and_last] # 中間のデータをフィルタリング
else:
road_coords_without_infras = road_coords
# 指定座標(point)に最も近い座標を取得
nearest_point = min(road_coords_without_infras, key=lambda x: Point(x).distance(Point(point)))
if nearest_point == (135.1666045, 34.699294):
pass
return nearest_point
ある程度補正できましたがまだまだ凹凸がある状態です。

国の道路傾斜の基準にあわせる
道路傾斜の基準は国の道路構造令の第十六条に書かれており、生活道路を除く一般的な道路は「最大10%」とされています。これは100mあたり最大10mの勾配までならOKという事になります。
この基準に適合するように補正をかけます。
from geopandas import GeoDataFrame
from pandas import Series
from geopy.distance import geodesic
# 国基基準だと100mあたり10%までOKだが一旦8%とする。
METER_AND_ELEVATION_RATIO = 0.08
# 国の基準に合わせて標高値を補正する
# gdf = 補正するLineStringと標高値を含むGeoDataFrame
def generate(gdf: GeoDataFrame) -> Series:
def func(row):
line = row.geometry
elevations = row.elevation
slope_per_meter_list = []
for index, point in enumerate(line.coords):
elevation = elevations[index]
if index + 1 < len(line.coords):
next_point = line.coords[index + 1]
next_point_elevation = elevations[index + 1]
distance = geodesic((point[1], point[0]), (next_point[1], next_point[0])).meters
elevation_diff = abs(elevation - next_point_elevation)
slope_per_meter = elevation_diff / distance
slope_per_meter_list.append(slope_per_meter)
if slope_per_meter > METER_AND_ELEVATION_RATIO:
if elevation < next_point_elevation:
adjust_next_elevation = elevation + (distance * METER_AND_ELEVATION_RATIO)
else:
adjust_next_elevation = elevation - (distance * METER_AND_ELEVATION_RATIO)
if adjust_next_elevation < 0:
adjust_next_elevation = 0
elevations[index + 1] = adjust_next_elevation
return elevations
series = gdf.apply(func, axis=1)
return series
補正をかけるとだいぶ道路のような形状になりました。

橋の区間を補正
OpenStreetMapから橋の区間も取得できるのでトンネルと同様の手順で線形的に補正をかけます。

ここまでの補正で道路の標高値を計算する事ができました。
この標高値から「勾配がついている道路」と「波打つようなの坂道」の判定を行います。
余談ですが、国土地理院から標高値を取得する場合はAPIを使わずにローカルに環境を作っておく事をおすすめします。
勾配がついている道の評価
峠の醍醐味は勾配です。
勾配の評価方法は簡単で、候補区間内で標高値の高低差を求めてその値の大きさから勾配がついているかどうかを判別します。ですが勾配はただついていればいいものではなく、ある一定以上は運転しづらくなってしまいます。そのため事前に運転しやすい高低差の範囲を決めて、その範囲内に収まるなら評価を上げるようにしました。今回は高低差が30~300mの範囲内を良い勾配と評価し500mを超える場合は評価値を下げるようにしました。
| 勾配が大きすぎる道 | ほどよい勾配の道 |
|---|---|
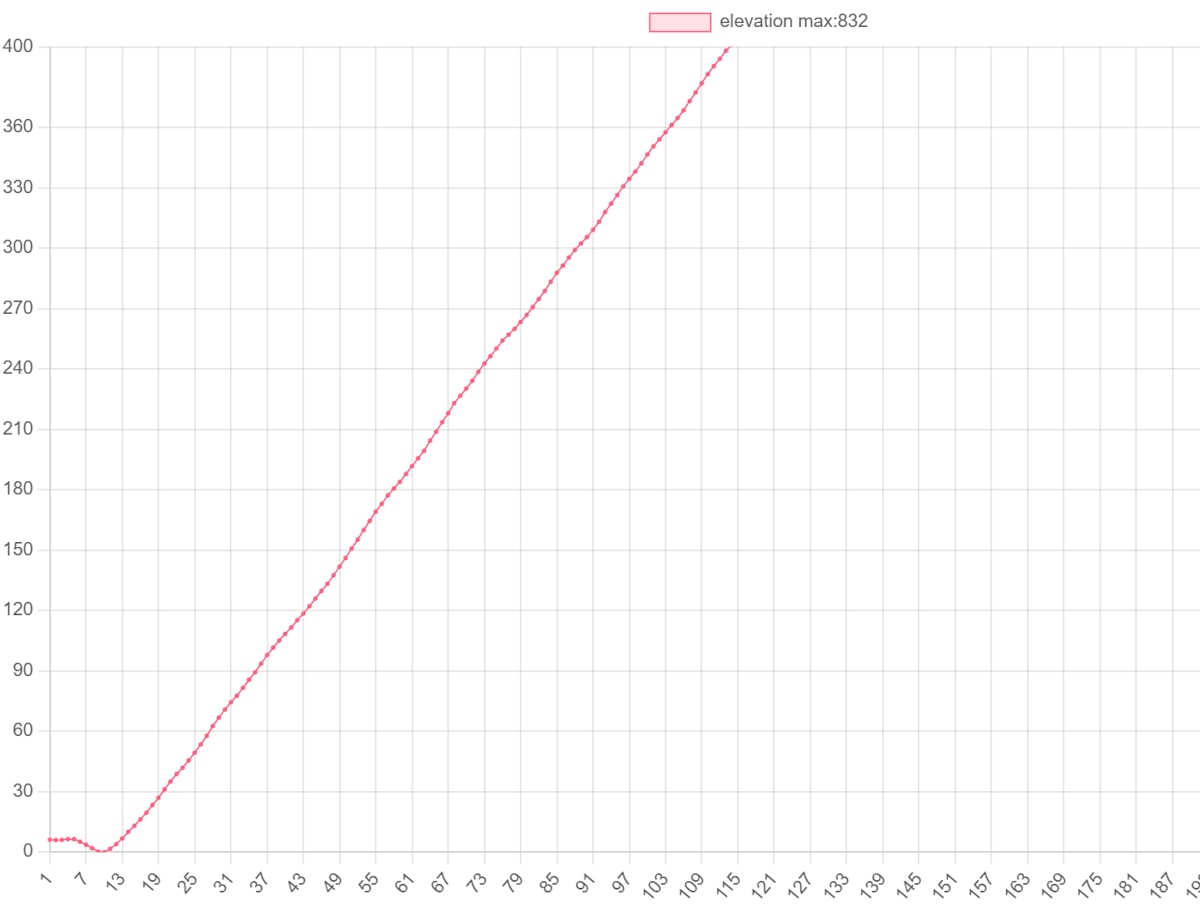 |
 |
# 勾配を評価する
def generate(gdf: GeoDataFrame) -> Series:
def func(row):
# 標高の高低差を求める。
elevation = row['elevation']
min_elevation = min(elevation)
max_elevation = max(elevation)
elevation_height = max_elevation - min_elevation
# 高低差が30m-300mの範囲を0.4~1の範囲に変換
old_min, old_max = 30, 300
new_min, new_max = 0.4, 1
initial_value = 0
if elevation_height >= old_max:
initial_value = 1
else:
initial_value = convert_range(elevation_height, old_min, old_max, new_min, new_max)
# 高低差が500m以上の場合は評価値を減らす
subtrahend = 0
if elevation_height >= 500:
old_min, old_max = 500, 1000
new_min, new_max = 0.5, 1
if elevation_height >= old_max:
subtrahend = 1
else:
subtrahend = convert_range(elevation_height, old_min, old_max, new_min, new_max)
return initial_value - subtrahend
series = gdf.apply(func, axis=1)
return series
def convert_range(value, old_min, old_max, new_min, new_max):
return ((value - old_min) / (old_max - old_min)) * (new_max - new_min) + new_min
波打つような坂が多い道を評価
波打つような坂道とはz軸方向にうねうねしている道の事でです。
こういった道は上り区間、下り区間といったように分ける事ができて自動車の特性が大きく現れます。たとえば、FF(前輪駆動)なら下り区間でトラクションがかかり、FR(後輪駆動)なら上り区間でトラクションがかかります。そのため、こういった上り下り区間が混じっている道は駆動方式に関係なく楽しめる道という事にもなります。
| 単純な坂 | 波打つような坂 |
|---|---|
 |
 |
この上りと下り区間の数を計算します。
計算方法はScripyという数値解析ライブラリでデータ内のプロミネンス(データの中で尖っている部分)を求めその数の合計を求めます。プロミネンスについてはこちら記事がとてもわかりやすいです。
以下は候補区間の標高値から尖っているポイントを求めた物です。

elevations= [0, 10, 4, 4, 3, 2, 1, 5, 4, 3, 2, 1, 1, 1, ,1......]
distance = 3
prominence = 5
# 上り区間のpeak値を取得
peaks, _ = find_peaks(elevations, distance=distance, prominence=prominence)
count = len(peaks)
print(count)
プロミネンスはデータの尖っている部分を検出するだけなのでそのまま使用すると凹みが検出されません。
そのため逆転したデータを使用する事で凹みを検出します。

elevations= [0, 10, 4, 4, 3, 2, 1, 5, 4, 3, 2, 1, 1, 1, ,1......]
distance = 3
prominence = 5
# 上り区間のpeak値を取得
peaks, _ = find_peaks(elevations, distance=distance, prominence=prominence)
# 下り区間のpeak値を取得
elevations_inverted = np.max(elevations) - elevations
peaks_inverted, _ = find_peaks(elevations_inverted, distance=3, prominence=5)
print(len(peaks) + len(peaks_inverted))
これで上り区間と下り区間の数を求める事ができました。
この区間数が多い道が「波打つような坂が多い道」という事になります。
多様なコーナーとストレートが混ざった道を評価する
峠道と思い浮かべるとコーナーのRが大きい道を想像すると思いますが、ただ大きいだけだと単調で運転してつまらない道になってしまいます。
レーシングゲームをやった事がある方ならわかると思いますが、コーナーの1つ1つに適切なアプローチ方法があり、それらはコーナー直前の状態によって変わります。なので多様な形状をしている道ほどアプローチ方法が多くなり楽しい道となります。
このような道を判別するために多様なコーナーとストレートが適切に混ざり込んだ道を判別します。
計算方法としては、道路区間のLineStringから高速コーナー、中速コーナー、低速コーナー、ストレートの区間を求めそれらの区間距離の割合が近い道ほど評価が上がるようにします。
上記を求めるにはまず候補区間を自動車が走行するために必要な前輪の舵角を求め、その舵角とステアリングギア比からステアリング回転量のを求め、その回転量からコーナーとストレート区間に分割し、その区間毎の合計距離の割合が近い場合に評価されるようにします。
指定区間を自動車が走行するために必要なステアリング回転量の推移を求める
ステアリング回転量は3座標毎に求めます。
区間道路のLineStringから先頭3座標を抜き出してその3座標を通る円の半径を求めます。これと車の前輪に舵角がついたときに車が円を描いて回転する際の円の半径がイコールになる時の前輪の舵角量を求めます。この舵角量と車のステアリングギア比の積を求める事で車が3座標間を走行するのに必要なステアリング回転量を求める事ができます。
上記処理を1座標ずつずらしながら全座標の計算を行う事で指定区間内のステアリング回転量の推移が求まります。
| 指定区間の先頭3座標を通る円の半径 | 車の前輪に舵角がついたときに車が円を描いて回転する際の円の半径 |
|---|---|
 |
 autoexeさんの「チューニングを楽しむための動的感性工学概論 §11」から引用 autoexeさんの「チューニングを楽しむための動的感性工学概論 §11」から引用
|
こちらは3座標を一般的なコンパクトカーが走行するために必要なステアリング回転量を計算するサンプルです。
import numpy as np
# 3座標を通過するステアリングの角度を計算するサンプル
def main():
# 自動車の情報(コンパクトカーを想定)
wheel_base = 2.5 # ホイールベース(m)
steering_ratio = 15 # ステアリングギア比(ステアリングと前輪タイヤの回転比率)
# 3点を通る円の中心と半径を計算
p1 = np.array([0, 0])
p2 = np.array([1, 1])
p3 = np.array([2, 0])
center, radius = calc_circle_center_and_radius(p1 ,p2, p3)
# ステアリングの切れ角を計算
steering_angle = calc_steering_angle(wheel_base, radius, steering_ratio)
# ステアリングの回転方向を計算(左、前、右)
direction = calc_direction(p1, p2, p3)
print(f"ステアリングの切れ角: {steering_angle:.2f}°, 回転方向: {direction}")
# 3点を通る円の中心の座標と半径を計算
def calc_circle_center_and_radius(p1, p2, p3):
temp = p2[0]**2 + p2[1]**2
bc = (p1[0]**2 + p1[1]**2 - temp) / 2
cd = (temp - p3[0]**2 - p3[1]**2) / 2
det = (p1[0] - p2[0]) * (p2[1] - p3[1]) - (p2[0] - p3[0]) * (p1[1] - p2[1])
if abs(det) < 1.0e-10:
# 3点が直線上にある場合はエラー
raise ValueError("Points are collinear")
# 円の中心 (cx, cy)
cx = (bc * (p2[1] - p3[1]) - cd * (p1[1] - p2[1])) / det
cy = ((p1[0] - p2[0]) * cd - (p2[0] - p3[0]) * bc) / det
# 半径
radius = np.sqrt((cx - p1[0])**2 + (cy - p1[1])**2)
return (cx, cy), radius
# ステアリング切角を計算
def calc_steering_angle(wheelbase, radius, steering_ratio):
tire_angle = 90 - (np.arccos(wheelbase / radius) * (180 / np.pi)) # タイヤの舵角を計算
steering_wheel_angle = tire_angle * steering_ratio # タイヤの舵角をステアリングの舵角に変換
return steering_wheel_angle
# ステアリングの回転方向を計算
def calc_direction(pm1, p2, p3):
det = (p2[0] - pm1[0]) * (p3[1] - p2[1]) - (p2[1] - pm1[1]) * (p3[0] - p2[0])
if det > 0:
direction = "left"
elif det < 0:
direction = "right"
else:
direction = "straight"
return direction
// 上記ロジックで求めた指定区間のLineString[A, B, C, D, E]のステアリング回転量の推移データ
[
{
start: [137.0004442, 35.3744692],
center: [137.0004336, 35.3745886],
end: [137.00041195, 35.37470605],
steering_angle: 1.9882090936,
radius: 1080.6678508533,
distance: 26.4795107773,
direction: "left",
},
{
start: [137.00041195, 35.37470605],
center: [137.0003903, 35.3748235],
end: [137.00037985, 35.3749338],
steering_angle: 0.5740575027,
radius: 3742.8164974385,
distance: 25.4709822213,
direction: "right",
},
{
start: [137.00037985, 35.3749338],
center: [137.0003694, 35.3750441],
end: [137.00043275, 35.3751771],
steering_angle: 59.5237431153,
radius: 36.1252554475,
distance: 28.1335727288,
direction: "right",
},
];
高速コーナー、中速コーナー、低速コーナー、ストレートの区間を求めて複雑性の高い道を求める
直前に求めたステアリング回転量の推移から高速コーナー、中速コーナー、低速コーナー、ストレートの区間を求めます。
ちなみに高速コーナーとはアクセル全開で踏み切れるコーナーの事をさし、中速コーナーとはハーフアクセルかライトブレーキを必要とするコーナーをさし、低速コーナーとは直前でABSを必要とするコーナーの事をさします。
計算方法は、直前で求めたステアリング回転量の推移から連続する回転方向でグループ化し、グループ毎に回転量が最も大きい値を抜き出します。その値からグループが高速コーナー、中速コーナー、低速コーナー、ストレートかどうかの判別を行い、この4要素毎の合計距離の大きさが近い道が複雑性の高い道となります。
コードは長いので折りたたみます。
ステアリング回転量の推移データから連続するステアリング回転方向毎に右コーナー、左コーナー、ストレートでグループ化
# 3点のステアリング回転量の推移の情報から右コーナー、左コーナー、ストレートの区間を作成する
STRAIGHT_DISTANCE = 100 # ストレートの区間は100m続く場合のみストレートとする。100m以下の場合は前後のコーナーに分配して結合する。
STRAIGHT_ANGLE = 7 # ストレートの最大ステアリング切れ角
def generate(gdf: GeoDataFrame) -> Series:
def func(row):
# 連続する左コーナー、右コーナー、ストレートをグループ化する
sections = group_continuous_section(row['steering_wheel_angle_info'])
# ストレート区間が100m未満の場合は半分に分割して前後のセクションと結合する ※1
sections = merge_min_straight_section(sections)
# # 連続する同一方向のセクションをマージ(※1で結合した場合に同一方向のコーナーが連続する場合があるため)
sections = merge_continuous_section_section(sections)
# 扱いやすい形に整形
datas = []
for section in sections:
steering_angle_info = section['steering_angle_info']
# セクション内の座標を1つにまとめる
points = []
for x in steering_angle_info:
points.append(x['start'])
points.append(x['center'])
points.append(x['end'])
points = list(dict.fromkeys(points))
# セクションの距離を計算
distance = 0
for i in range(len(points) - 1):
distance += geodesic(reversed(points[i]), reversed(points[i+1])).meters
# ステアリング角度の最大値、平均値を取得
max_steering_angle = max(steering_angle_info, key=lambda x: x['steering_angle'])['steering_angle']
avg_steering_angle = sum([x['steering_angle'] for x in steering_angle_info]) / len(steering_angle_info)
datas.append({
'max_steering_angle': max_steering_angle,
'avg_steering_angle': avg_steering_angle,
'elevation_height_and_distance_ratio': elevation_height / distance,
'section_type': section['type'],
'steering_direction': steering_angle_info[0]['direction'],
'points': points,
'section_info': steering_angle_info,
'distance': distance,
'elevation_height': elevation_height,
})
return datas
series = gdf.apply(func, axis=1)
return series
# 3座標から求めたステアリング回転量の情報から、ステアリングの回転方向が連続するものをグループ化して左コーナー、右コーナー、ストレートのグループを作る
def group_continuous_section(target):
# ステアリングの方向が変わる毎にグループ化
old_direction = target[0]['direction']
sections = []
# 右左コーナーの情報
section_work = [target[0]]
for i in range(1, len(target)):
current_segment = target[i]
angle = current_segment['steering_angle']
distance = current_segment['distance']
direction = current_segment['direction']
if angle < STRAIGHT_ANGLE:
direction = 'straight'
if direction == old_direction:
section_work.append(current_segment)
else:
sections.append({'type': old_direction, 'steering_angle_info': section_work})
section_work = [current_segment]
old_direction = direction
# 最後の未処理のセグメントを追加
if len(section_work) > 0:
sections.append({'type': old_direction, 'steering_angle_info': section_work})
return sections
# 短いストレート区間をコーナーセクションにマージ
def merge_min_straight_section(sections):
# ストレート区間が100m未満の場合は半分に分割して前後のコーナーと結合する
adjusted_sections = copy.deepcopy(sections)
is_not_exists_min_straight = True
while is_not_exists_min_straight:
# ストレートを抽出
straights = [x for x in adjusted_sections if x['type'] == 'straight']
# 100m以下のストレートを抽出
min_straights = [x for x in straights if sum([y['distance'] for y in x['steering_angle_info']]) < STRAIGHT_DISTANCE]
if len(min_straights) == 0:
is_not_exists_min_straight = False
break
min_straight_first = min_straights[0]
# 100m未満の先頭indexを取得
min_straight_first_index = adjusted_sections.index(min_straight_first)
steering_angle_info = min_straight_first['steering_angle_info']
# 前後のコーナーを取得
if min_straight_first_index == 0:
# 先頭のコーナーの処理
next_section = copy.deepcopy(adjusted_sections[min_straight_first_index + 1])
next_section['steering_angle_info'] = steering_angle_info + next_section['steering_angle_info']
adjusted_sections[min_straight_first_index + 1] = next_section
elif min_straight_first_index == len(adjusted_sections) - 1:
# 末尾のコーナーの処理
previous_section = copy.deepcopy(adjusted_sections[min_straight_first_index - 1])
previous_section['steering_angle_info'] += steering_angle_info
adjusted_sections[min_straight_first_index - 1] = previous_section
else:
if(len(steering_angle_info)) >= 2:
# 前後のコーナーにマージ
previous_section = copy.deepcopy(adjusted_sections[min_straight_first_index - 1])
next_section = copy.deepcopy(adjusted_sections[min_straight_first_index + 1])
# 厳密にストレートの距離の半分を分割するべきだが、一旦は要素数から分割
previous_section['steering_angle_info'] += steering_angle_info[:len(steering_angle_info)//2]
next_section['steering_angle_info'] = steering_angle_info[len(steering_angle_info)//2:] + next_section['steering_angle_info']
adjusted_sections[min_straight_first_index - 1] = previous_section
adjusted_sections[min_straight_first_index + 1] = next_section
else:
# 1件だけの場合は直前のコーナーにマージ
previous_section = copy.deepcopy(adjusted_sections[min_straight_first_index - 1])
previous_section['steering_angle_info'] += steering_angle_info
adjusted_sections[min_straight_first_index - 1] = previous_section
# ストレートを削除
adjusted_sections.remove(min_straight_first)
return adjusted_sections
# 連続する同一方向のコーナーをマージ
# 同じ方向のコーナーが連続する場合は結合する。
def merge_continuous_section_section(road_sections):
merged_lst = []
i = 0
target_sections = road_sections
while i < len(target_sections):
current_section = target_sections[i].copy() # 現在のセクションをコピーして使用
# 次のセクションが同じタイプか確認
while i + 1 < len(target_sections) and target_sections[i]['type'] == target_sections[i + 1]['type']:
# 次のセクションが同じタイプであれば、steering_angle_infoを結合
current_section['steering_angle_info'] += target_sections[i + 1]['steering_angle_info']
i += 1 # 次のセクションをスキップ
# 結合したセクション(または単一のセクション)をリストに追加
merged_lst.append(current_section)
i += 1 # 次のセクションに移動
return merged_lst
コーナーとストレートの区間情報から、高速コーナー、中速コーナー、低速コーナー、ストレートの区間距離を求めてその割合を求める。
# 回転量7°以下はストレートとして扱う
# 高速コーナーの回転量の範囲 7~45°
HEIGHT_CORNER_ANGLE_MIN = 7
HEIGHT_CORNER_ANGLE_MAX = 45
# 中速コーナーの回転量の範囲 45°~80°
MEDIUM_CORNER_ANGLE_MIN = 45
MEDIUM_CORNER_ANGLE_MAX = 80
# 低速コーナーの回転量の範囲 80°~
LOW_CORNER_ANGLE_MIN = 80
# 各コーナー種別の間のゾーン値(±5度)
# コーナー種別が切替る間を段階的に評価するために使用
CORNER_TRANSITION_ZOON = 5
def generate(gdf: GeoDataFrame) -> tuple[Series, Series, Series]:
def func(x):
road_section = x['road_section']
corner_week_distance = 0
corner_medium_distance = 0
corner_strong_distance = 0
corner_none_distance = 0
# 各コーナー種別の距離を計算
for item in road_section:
angle = item['max_steering_angle']
distance = item['distance']
if item['section_type'] == 'straight':
corner_none_distance += distance
else:
if WEEK_CORNER_ANGLE_MIN <= angle < MEDIUM_CORNER_ANGLE_MIN:
# 弱コーナーの計算
if angle < (WEEK_CORNER_ANGLE_MAX - CORNER_TRANSITION_ZOON):
corner_week_distance += distance # 完全に「弱」の領域
else:
# 境界付近は重み付け
transition_ratio = (WEEK_CORNER_ANGLE_MAX - angle) / CORNER_TRANSITION_ZOON
corner_week_distance += distance * transition_ratio
corner_medium_distance += distance * (1 - transition_ratio)
elif MEDIUM_CORNER_ANGLE_MIN <= angle < STRONG_CORNER_ANGLE_MIN:
# 中コーナーの計算
if angle < (MEDIUM_CORNER_ANGLE_MAX - CORNER_TRANSITION_ZOON):
corner_medium_distance += distance # 完全に「中」の領域
else:
# 境界付近は重み付け
transition_ratio = (MEDIUM_CORNER_ANGLE_MAX - angle) / CORNER_TRANSITION_ZOON
corner_medium_distance += distance * transition_ratio
corner_strong_distance += distance * (1 - transition_ratio)
elif STRONG_CORNER_ANGLE_MIN <= angle:
# 強コーナーの計算
corner_strong_distance += distance # 完全に「強」の領域
# 総距離で正規化
total_distance = corner_week_distance + corner_medium_distance + corner_strong_distance + corner_none_distance
score_corner_week = corner_week_distance / total_distance
score_corner_medium = corner_medium_distance / total_distance
score_corner_strong = corner_strong_distance / total_distance
score_corner_none = corner_none_distance / total_distance
# バランスを評価
values = [score_corner_week, score_corner_medium, score_corner_strong, score_corner_none]
k = 0.4
std_dev = np.std(values)
score = 1 - (std_dev / k)
return score
results = gdf.apply(func, axis=1, result_type='expand')
return results[0]
上記ロジックで各コーナーとストレートの区間を求めたものがこちらになります。
| 近所の道 | 近所の道を各コーナーとストレートの区間に分割したもの |
|---|---|
 |
 |
この4要素の区間距離の割合が近い道が平面上で複雑性がありコーナーへのアプローチ方法が多い道という事になります。
抽出された道
これまでのロジックで東京周辺の峠道を抽出したものがこちらです。
色が濃い所が「イニシャルDのような峠道」の評価値が高い道です。
上位1~10にはマーキングしています。

抽出された道は群馬県に多くイニシャルDの聖地も多いので良い感じです。
 榛名山周辺。右上の薄い所が藤原拓海のホームスポットだが複雑性が少なく単調な道と評価され上位10に含まれなかった。 榛名山周辺。右上の薄い所が藤原拓海のホームスポットだが複雑性が少なく単調な道と評価され上位10に含まれなかった。
|
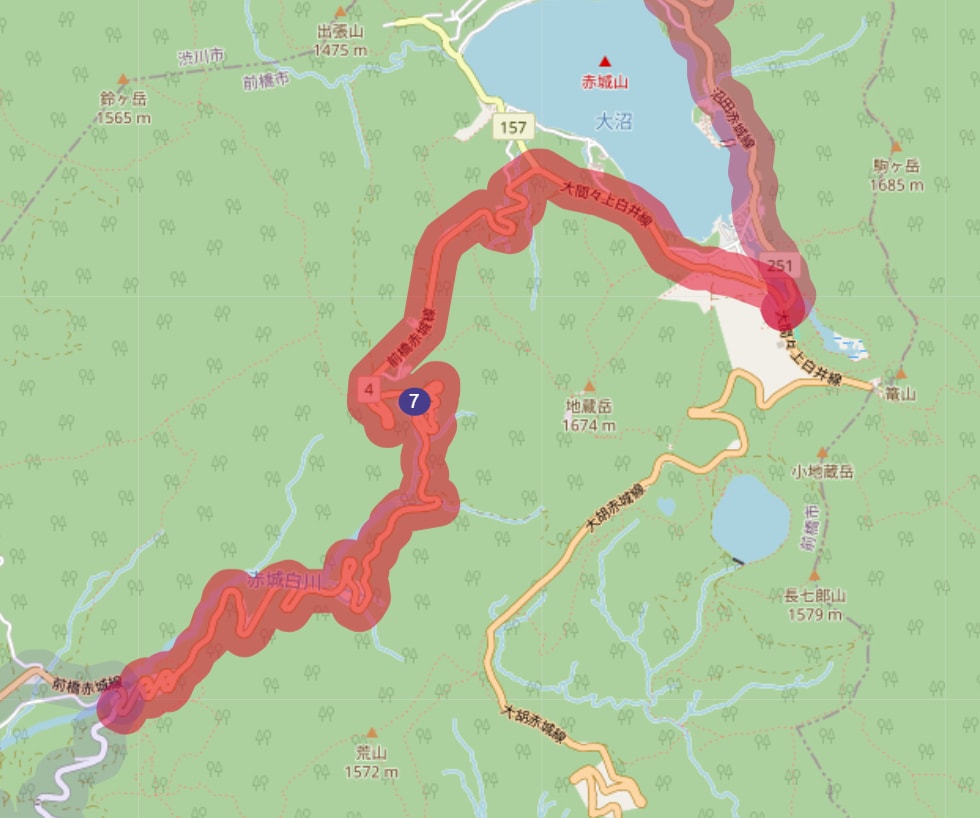 レッドサンズの赤城山は上位10に含まれた。 レッドサンズの赤城山は上位10に含まれた。
|
 ナイトキッズの妙義山は上位10で含まれた。 ナイトキッズの妙義山は上位10で含まれた。
|
 インパクトブルーの碓氷峠は単調な道と評価され上位10に含まれなかった。 インパクトブルーの碓氷峠は単調な道と評価され上位10に含まれなかった。
|
実際に走ってみた
地元の愛知県で「イニシャルDのような峠道」の特徴が高い道を実際に運転してみました。
結論から言うと、ラリーに使用された道や暴走行為を控えるような標識がある道が抽出され良い結果となりました。

1. 本宮山スカイライン
新城ラリーで使われた実績のある道
https://www.youtube.com/watch?v=gBQaaCD0Rjc
2. 三河湾スカイライン
有名な走りスポット。
https://itest.5ch.net/hayabusa9/test/read.cgi/news/1607628104/l-
3. 矢作ダム
90年代の走りスポットで有名な所。
http://www.hashiriya.jp/bbs2/test/read.cgi/citokai/1081382495/
4. 茶臼山
サーキット禁止?の看板が経っている道。

アノレプス乙女さん口コミから引用
ビュワーで確認
こちらから日本全国の「イニシャルDのような峠道」をご覧いただけます。 各峠を3Dで確認する事もできます。
作ってみて思った事
自分の感覚をプログラムで再現するのは楽しいですね。仕事では絶対に味わえない感覚でした。
現地調査を何度も繰り返したおかげでかなりいい感じ精度がでたのと、ロジックが仕上がっていくたびに空間を支配できているような気分になれて楽しかったです。
おわりに
最後までお読みいただきありがとうございました。
完成したコードはこちらでご覧いただけます。
Discussion