Blink-tree についてのメモ

使われているテクニックメモ

• 可変長のデータの扱い
  • 構造体とメモリ上のデータ構造が一致していない
• buffer pool での hash table の利用
• phase-fair reader-writer lock
• メモリマップトファイル
  • 管理用の 1 ページ分のみで使用
• sched_yield
  • spinlock の実装で使用
• librarian slot
  • 挿入に備えて用意されている空きスロット
  • DB 一般用語では無さそう

BufMgr

create

https://github.com/PLW/blink-tree-logic/blob/ee67d3c7e434fb4edebe061b7cc77bf2aff25df4/bufmgr.cpp#L89C13-L89C27

page=0 は管理用

https://github.com/PLW/blink-tree-logic/blob/ee67d3c7e434fb4edebe061b7cc77bf2aff25df4/bufmgr.cpp#L182-L192

tree の level は最低 2 つ必要

https://github.com/PLW/blink-tree-logic/blob/ee67d3c7e434fb4edebe061b7cc77bf2aff25df4/bufmgr.cpp#L194-L221

大量 insert & find テスト

以下のようなテストケースを作成。

func TestBLTree_insert_and_find_many(t *testing.T) {
	_ = os.Remove(`data/bltree_insert_and_find_many.db`)
	mgr := NewBufMgr("data/bltree_insert_and_find_many.db", 15, 48)
	bltree := NewBLTree(mgr)

	num := uint64(160000)

	for i := uint64(0); i < num; i++ {
		bs := make([]byte, 8)
		binary.BigEndian.PutUint64(bs, i)
		if err := bltree.insertKey(bs, 0, [BtId]byte{}, true); err != BLTErrOk {
			t.Errorf("insertKey() = %v, want %v", err, BLTErrOk)
		}
	}

	for i := uint64(0); i < num; i++ {
		bs := make([]byte, 8)
		binary.BigEndian.PutUint64(bs, i)
		if _, foundKey, _ := bltree.findKey(bs, BtId); bytes.Compare(foundKey, bs) != 0 {
			t.Errorf("findKey() = %v, want %v", foundKey, bs)
		}
	}
}

→実行にかかる時間は概ね 0.15s 前後なので insert & find 合わせて 2,133,333.333 ops/sec

ちなみにキーに用いている uint64 を LittleEndian で符号化すると、1s 前後かかるので 320,000.000 ops/sec まで落ちる。
(内訳: insert で 0.5s~、find で 0.4s~)

BigEndian で符号化するとキーは単調増加するので insert, find ともに常に同じページかつキーの挿入先 slot も常に一番後ろの位置となり、ファイル I/O はページが溢れて split する際に限られる。
対して、LittleEndian で符号化すると、先頭のバイトが256周期で0になり、キーの挿入先ページ & slot が巻き戻って buffer pool の入れ替えや slot の並び替えが起こるから性能が落ちるのだと思われる。

並行 insert & find テスト

gorountine 7 つで並行処理を試す。

func TestBLTree_insert_and_find_concurrently(t *testing.T) {
	log.SetOutput(io.Discard)
	_ = os.Remove(`data/insert_and_find_concurrently.db`)
	mgr := NewBufMgr("data/insert_and_find_concurrently.db", 15, 16*7)

	routineNum := 7
	keyTotal := 1600000

	wg := sync.WaitGroup{}
	wg.Add(routineNum)

	keys := make([][]byte, keyTotal)
	for i := 0; i < keyTotal; i++ {
		bs := make([]byte, 8)
		binary.BigEndian.PutUint64(bs, uint64(i))
		keys[i] = bs
	}

	start := time.Now()
	for r := 0; r < routineNum; r++ {
		go func(n int) {
			bltree := NewBLTree(mgr)
			for i := 0; i < keyTotal; i++ {
				if i%routineNum != n {
					continue
				}
				if err := bltree.insertKey(keys[i], 0, [BtId]byte{}, true); err != BLTErrOk {
					t.Errorf("in goroutine%d insertKey() = %v, want %v", n, err, BLTErrOk)
				}
			}

			wg.Done()
		}(r)
	}
	wg.Wait()
	t.Logf("insert %d keys concurrently by big endian cost %v", keyTotal, time.Since(start))

	wg = sync.WaitGroup{}
	wg.Add(routineNum)

	start = time.Now()
	for r := 0; r < routineNum; r++ {
		go func(n int) {
			bltree := NewBLTree(mgr)
			for i := 0; i < keyTotal; i++ {
				if i%routineNum != n {
					continue
				}
				if _, foundKey, _ := bltree.findKey(keys[i], BtId); bytes.Compare(foundKey, keys[i]) != 0 {
					t.Errorf("findKey() = %v, want %v, i = %d", foundKey, keys[i], i)
				}
			}

			wg.Done()
		}(r)
	}
	wg.Wait()

	t.Logf("find %d keys by big endian cost %v", keyTotal, time.Since(start))
}

=== RUN   TestBLTree_insert_and_find_concurrently
    bltree_test.go:145: insert 1600000 keys concurrently by big endian cost 15.540460375s
    bltree_test.go:168: find 1600000 keys by big endian cost 3.10690175s
--- PASS: TestBLTree_insert_and_find_concurrently (18.67s)

• insert: 103,225.806 ops/sec
• find: 516,129.032 ops/sec

時間はブレが大きいので、参考程度(特にinsert は 10s - 20s でブレる)

並列数を1にすると insert も find もそれぞれ 3s ほどなので、goroutine 間で latch や buffer pool の取り合いが起きている可能性あり。

メモ

LittleEndian で試すとバグる(fix済)

• 50000 件挿入したあたりで固まる
• たまに insert 直後の find で違うキーが返ってくることがある

    bltree_test.go:132: [goroutine1] i= 48000, duration = 180.034958ms
    bltree_test.go:132: [goroutine3] i= 46000, duration = 183.003417ms
    bltree_test.go:132: [goroutine2] i= 47000, duration = 184.40625ms
    bltree_test.go:132: [goroutine6] i= 50000, duration = 188.704875ms
    bltree_test.go:128: [goroutine4] findKey() = [109 190 0 0 0 0 0 0], want [109 189 0 0 0 0 0 0]
    # ここでスタック

調査メモ

ログを仕込んだところ、写経コードにおける以下の箇所でロックが取れずにスタックしているらしいことがわかった。
(SpinLock の実装に、スピン数が一定回数に達したときにログを出すように仕込んだ)

https://github.com/PLW/blink-tree-logic/blob/ee67d3c7e434fb4edebe061b7cc77bf2aff25df4/bufmgr.cpp#L499

追加で調べたところ、buffer pool の victim 対象を探すループが回り続けていた。

https://github.com/PLW/blink-tree-logic/blob/ee67d3c7e434fb4edebe061b7cc77bf2aff25df4/bufmgr.cpp#L544

このループは1つ目のコードを通過しロックを取った後の箇所なので、ロックを握ったまま無限ループになっている模様。

BugMgr のコンストラクタ引数の3つ目が buffer pool size なので、これに大きな値を指定したところ、処理が完了するようになった。

mgr := NewBufMgr("data/insert_and_find_concurrently.db", 15, 1024)

ただ pool size が小さい場合に findKey が失敗することがある点についてはなにかバグが潜んでいそう。

怪しい箇所

このロックのリリースタイミングが早いのでは？

https://github.com/PLW/blink-tree-logic/blob/ee67d3c7e434fb4edebe061b7cc77bf2aff25df4/bufmgr.cpp#L605

その直後の latchlink の中では evict 対象のページに関する情報を保持する LatchSet というクラスを再利用するための初期化処理をするが、上記のロックのリリースがされると複数のクライアントが同時に LatchSet を初期化してしまいそう。

→このロックのリリースタイミングを latchlink 後に変更したところ findKey の失敗エラーが起こらなくなった(本当にこれだけの理由なのかは、不明)

並行 insert & find テストの振り返り

• findKey でおかしい値が返されるバグについてはロックリリースタイミング修正後に再発はしていない
• buffer pool 操作のロック範囲を狭めるための hash table の問題が2点見つかった
  • 同一のハッシュ値を持つページのlatch情報を linked list で管理している箇所で不正な循環参照を起こしていた
    • →修正済
  • buffer pool サイズの指定が小さすぎて、上記 hash table のエントリ数が並行数よりも小さい場合、evict 対象を特定する際にロックが取れずにスタック
    • →並行数 <= hash table のエントリ数(buffer pool サイズによって決まる)、となるように変更した結果、スタックしなくなった
• 実行速度
  • buffer pool サイズを増やした結果、挿入するキーを BigEndian、LittleEndian どちらで符号化してもあまり結果に差は出なくなった
    • insert は LittleEndian、find は BigEndian が速い傾向はある
  • LittleEndianの場合、並行数1よりも並行数7の方が速い
    • 160万件のinsert&findを試した
      • insert は並行数1=20s, 並行数7=7s
      • find は並行数1=12s, 並行数7=7s
  • →実行速度は go test で雑に見ているので、デバッグ落ち着いてきたらちゃんと計測する
    • 16万件の insert&find テストを再実行したら条件変わってないはずなのに 0.15s → 0.5s と変わるなど起きている
• db ファイルサイズは LittleEndian に比べて BigEndian 方式が2.5倍ほどになっていた
  • 常に右端のページがsplitしていくのでslotの充填率が低くなってそう

並行 insert & delete テスト

gorountine 7 つで並行処理を試す。
7つの goroutine で自分が担当するキーをinsert & 2回に1回 deleteする。

func TestBLTree_deleteManyConcurrently(t *testing.T) {
	log.SetOutput(io.Discard)
	_ = os.Remove("data/bltree_delete_many_concurrently.db")
	mgr := NewBufMgr("data/bltree_delete_many_concurrently.db", 15, 16*7)

	keyTotal := 1600000
	routineNum := 7

	keys := make([][]byte, keyTotal)
	for i := 0; i < keyTotal; i++ {
		bs := make([]byte, 8)
		binary.LittleEndian.PutUint64(bs, uint64(i))
		keys[i] = bs
	}

	wg := sync.WaitGroup{}
	wg.Add(routineNum)

	start := time.Now()
	for r := 0; r < routineNum; r++ {
		go func(n int) {
			bltree := NewBLTree(mgr)
			for i := 0; i < keyTotal; i++ {
				if i%routineNum != n {
					continue
				}
				if err := bltree.insertKey(keys[i], 0, [BtId]byte{}, true); err != BLTErrOk {
					t.Errorf("in goroutine%d insertKey() = %v, want %v", n, err, BLTErrOk)
				}

				if i%2 == (n % 2) {
					if err := bltree.deleteKey(keys[i], 0); err != BLTErrOk {
						t.Errorf("deleteKey() = %v, want %v", err, BLTErrOk)
					}
				}
			}

			wg.Done()
		}(r)
	}
	wg.Wait()
	t.Logf("insert %d keys and delete skip one concurrently. duration =  %v", keyTotal, time.Since(start))

	wg = sync.WaitGroup{}
	wg.Add(routineNum)

	start = time.Now()
	for r := 0; r < routineNum; r++ {
		go func(n int) {
			bltree := NewBLTree(mgr)
			for i := 0; i < keyTotal; i++ {
				if i%routineNum != n {
					continue
				}
				if i%2 == (n % 2) {
					if found, _, _ := bltree.findKey(keys[i], BtId); found != -1 {
						t.Errorf("findKey() = %v, want %v, key %v", found, -1, keys[i])
					}
				} else {
					if found, _, _ := bltree.findKey(keys[i], BtId); found != 6 {
						t.Errorf("findKey() = %v, want %v, key %v", found, 6, keys[i])
					}
				}
			}

			wg.Done()
		}(r)
	}
	wg.Wait()

	t.Logf("find %d keys. duration = %v", keyTotal, time.Since(start))
}

→うまく動くこともあるが、ページが壊れることもある

成功例

=== RUN   TestBLTree_deleteManyConcurrently
    bltree_test.go:290: insert 1600000 keys and delete skip one concurrently. duration =  8.371527833s
    bltree_test.go:319: find 1600000 keys. duration = 5.937712791s
--- PASS: TestBLTree_deleteManyConcurrently (14.34s)
PASS

本来存在すべきキーが無いというエラー発生例

=== RUN   TestBLTree_deleteManyConcurrently
    bltree_test.go:290: insert 1600000 keys and delete skip one concurrently. duration =  8.188417709s
    bltree_test.go:309: findKey() = -1, want 6, key [54 0 0 0 0 0 0 0]
    bltree_test.go:309: findKey() = -1, want 6, key [53 220 0 0 0 0 0 0]
    ...

New latch modes

3種類の独立したnode latchesを使い、それらの latch は __sync_fetch_and_xxx function family によって操作

• shareable: AccessIntent and exclusive: NodeDelete
  • tree から削除される前の空のノードにアクセスすること防ぐ
  • AccessIntent は親ノードから子ノードへの latch-coupling を使った search 中に取得
  • NodeDelete はノードを利用可能な free list に返す前の最終段階で取得
    • ノードの全てのポインタが削除され、AccessIntent がなくなるまでブロックされる
• shareable: ReadLock and exclusive: WriteLock
  • search 中に AccessIntent からの lock-coupling を使用して取得
• ParentModification exclusive latch
  • split や merge の際にノードのフェンスキーが親ノードから更新or削除されるまで保持
  • 親ノードのフェンスキーが更新される間、ノードの WriteLock を解放して並行処理ができる

ノードが削除された後、並行したツリー操作によってそのノードが参照されないことを保証するためのコストは、search 中のルートアクセス後にそれぞれのレベルにおいて 2 つのノード latch を取得する必要があること。

→ Insert/Delete時に latch upgrade や downgrade がないことやページ latch 実装の高い性能によってコストを軽減

Latch Compatibility Matrix

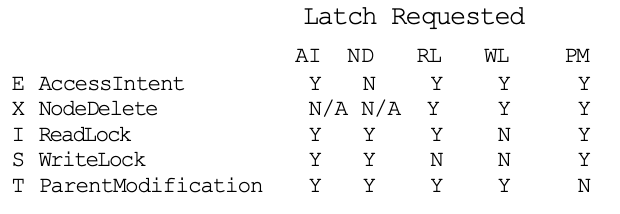
• 左側が先に取得された latch タイプ
• Y: latch 間で競合なし
• N: latch 間は競合
• N/A: ノードが削除されており latch 対象がない

latch モードは 5つで、3つの独立した latch に編成されている。

• latch1
  • AccessIntent
    • 親ノードの読み取り latch が解除後 AccessIntent は保持されたまま子ノードの ReacLock or WriteLock を取得
  • NodeDelete
    • ノードへのポインタが WriteLock でツリーから削除され、アクセスできなくなった際に取得
• latch2
  • ReadLock
  • WriteLock
• latch3
  • ParentModification
    • ノードの上位フェンス値の変更を親ノードに記録
    • 別の ParentModification とのみ互換性がない

Tree Operations

Search

• ツリーをルートからターゲットノードまで辿る間、親ノードの ReadLock は子ノードの AccessIntent の取得と latch-coupled
  • NodeDelete はツリーから全ての参照が削除された後にのみ取得されるため、AccessIntent の取得がブロックされることはない
• 子ノードの AccessIntent は子ノードの ReadLock/WriteLock の取得と latch-coupled
• ノードの上限フェンス値を超えるキーの要求は right sibling に向けられる
• 削除中の空のノードにアクセスすると、その left ノードへのリンクを使った sibling traversal をする

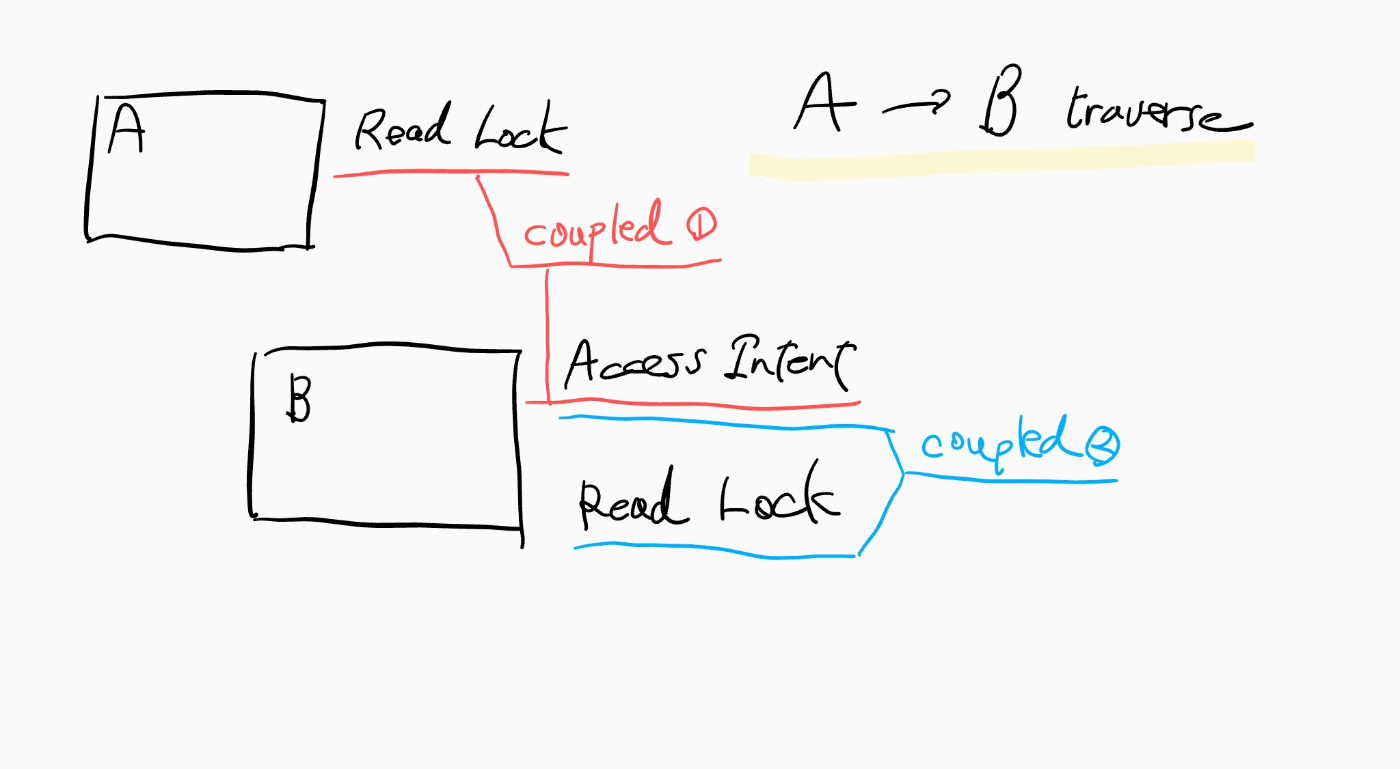
Update/Insert

• Search 時に取得した WriteLock 下にあるノードにキーを追加・更新し、WriteLock を解放
• 新しいキーがノードに入り切らない場合は、先に split

Split

• WriteLock に加えて ParentModification latch が取得される
  • 該当ノードに対する以前の Split/Consolidation が進行中の場合はブロックされる
    • ParentModification latch が取られているから
• コンテンツの上半分を新しい右ノードに分割し、元の左側のノードの WriteLock を解放
  • このノードも ParentModification latch
• 左ノードの新しいフェンス値と、新しい右ノードの上部フェンスキーが親ノードで更新
  • 親ノードが split した場合、左右のノードの親ノードが異なる可能性がある
• その後左右ノードの ParentModification latch 解除

Delete

• Search 時に取得した WriteLock 下にあるノードの該当キーに削除ビットを立てる
• ノードが空になったら right sibling と統合
• 上位フェンス値が削除された場合、祖父母ノードキーを修正
• ルートノードが単一の子ノードに縮小された場合、子ノードの内容で書き換え
  • "collapse the root node"

Consolidation

• 右ノードに対して WriteLock を取得
• 右ノードの情報で左側の統合対象ノードの値を書き換え
• 右ノードのリンクフィールドは左ノードに向ける
  • 後続の検索を左の連結ノードに誘導
• 左の連結ノードに対して ParentModification latch
• 左右ノードの WriteLock が解放
• 古い左ノードのフェンスキーは親ノードから削除 & 古い右ノードのフェンスキーは左ノードを指すようにする
• 左ノードの ParentModification 解放
• 削除された右ノードに対して NodeDelete latch と WriteLock latch を取得
• 右ノードを free listへ

Deleting Fence Keys

親ノードの上位フェンスキーでもある子ノードの上位フェンスキーを削除する時、2パターンの動作が可能。連結コードとその右ノードの親が異なる場合に発生。

• 1. 子ノード全体の削除を無視して、空ノードを残して後の Inserts で使えるようにする
  • Jaluta や Lomet などが採用している方法
  • Insert との対称性にかけ、ノードが空にならない祖父母のキースペースのパーティションは変更されない
  • 空ノードを削除するための定期的なツリーの再構成が必要
• 2. 親ノードのフェンスキーの変更を祖父母ノードまで伝搬
  • 親ノードのキー範囲が恒久的に狭まり、全ての再挿入キーが親の右ノードの下に押し込まれる
  • サンプルコードではこの方法を採用

abst

• Lehman & Yao の insertion 方法に対して対称性のある deletions を提案
• rare cases を除いて1つの lock で扱える
• 他の対称的な insertions and deletions アルゴリズムに比べて高い並行性がある

1. intro

• correctness を確保しつつできるだけ並行処理をするのがゴール
  • 並行処理: insertion, deletion, search

1.1 Previous Work

• first concurrent B-tree algorithms
  • a) 親ノード→子ノードと辿る際に、親ノードに対する lock リリース前に子ノードに対する lock を獲得
    • →lock-coupling
    • これをやらないと例えばノードの split と search が並行すると問題が起きる
  • b) 変更する必要のある highest node 以下の subtree 全体について他の writer を lock out する
    • severe disadvantage がある
• another algorithm
  • 楽観的に search-like な read locks を使って木構造を辿って leaf に対しては exclusive lock
    • split or merge がなければ、上記の locks だけで完了
    • split or merge が必要であれば normal protocol に fallback してやり直す

1.2 The Lehman and Yao Algorithm and Deletion

• Lehman & Yao の b-link tree は lock-coupling, subtree-locking を避けかつシンプルなので、筆者たちも元にしている
• 上記はノードの merge に対する provision がない
  • off-line で rebalance することを提案しているくらい

1.3 Symmetric Deletion Approach

• ノードの merge の際にright ノードから left ノードにデータを移した場合、right ノードに到達したプロセスはそれ以上進めなくなる
• 筆者の novel way では right ノードからデータを移しつつ outlink という right ノードから left ノードへの pointer を向ける

2. our algorithm

2.2 Locks

• Lehman & Yao の locking model では node 全体を 1 操作で read or write できることを仮定
  • 最初に lock せず reader プロセスがアクセスできることになるが、atomic な read or write ができることを仮定するのは reasonable ではない
• 筆者はより一般的な read lock, write lock を使う
• deletion のみ最大 2 つの lock を必要とする

2.3 The Locate Phase and the Decisive Operation

• locate phase: seach, insert, delete共通の first phase
  • lock 対象の leaf node を特定
  • lock-coupling は使わない
• decisive operation: leaf node に対する操作を実行

2.4 Restructuring

• ノードに対する adding or removing によって、ノードは too crowded or too sparse になる
  • split or merge で normalizing する
  • parent ノードに対する pointer の insert or remove も行い、さらなる split or merge が起こる可能性もある

2.4.1 Two-Phase Splits and Merges

• normalizing 中に parent を lock することを避けるために、split and merge を two stage で行う
• first stage: half-split or half-merge
  • この時点では parent 操作はしない
  • half-split 後もまだ 2 つのノードは1つの logical ノードとみなせる
  • half-merge は logically merging とみなせて、merge 元ノードへの downlink を merge 先ノードにリダイレクト
  • half-split or half-merge 完了したら全ての lock は release される
• second stage: add-link or remove-link
  • この操作は half-split or half-merge をしたノードの上位レベルの "appropriate" ノードに対して実施
  • sequential computation では apropriate ノードは常に unique な parent となるが、筆者の algorithm では work しない
    • several or no parents になり得るため
  • downlink の目的は better な基準を suggests すること
    • ?
  • add-link or remove-link 対象のノードは locale phase において一つ前に訪れた node となるのが普通だが、無理なこともある
    • 並行して parent ノードが split された場合など
    • top から新たに辿る必要がある

2.4.2 Changing the Height of the Structure

• top level を作成(the grow operation) することはできる
• 不要な top level を削除するのは難しすぎる
  • しかし、全てのアクションが不要な top level を辿るのは容認できない
  • →実際に削除はせず、search 時に避けるようにする
  • critic という絶えず実行されているプロセスは 1つ以上の downlink を持つ highest level を追跡している
    • 「1つ以上の...highest level」を fast level と呼ぶ
  • critic は情報を得るために read lock しか使わない
• fast level and top level の両方の leftmost ノードへのポインターは anchor の中で keep される
  • →全てのプロセスに知られるアドレス
  • 全てのアクションの locate phase は fast level の leftmost node において始まる
  • fast level の上位 level は fast level が埋まるまで使われない

2.5 Freeing Empty Nodes

• 空のノードへの pointer が全て削除されたら、そのノードは re-use 候補になる
• が、pointer が削除される前に該当ノードへの pointer を得ていたプロセスがあるかもしれないので、すぐに free にはできない
• 2つのアプローチ
  • drain technique
    • ノードへの pointer が存在していた時に始まった locate phase を持つプロセスが全て終わるまで free するのを delay
  • store information in every node
    • 全てのノードにその高さと leftmost separator key の情報を持たせる
    • プロセスはその情報を用いて become lost になったことを認識して引き返す
• appendix はどちらのアプローチのコードも含んでないが前者のほうが透過的

4.3 Blink-Trees

• 各ノードに high fence key と right neighbor への pointer をもたせる
• ノード分割を 2 つの独立したステップに分割
• split して right ノードが parent から参照されていないステップ
  • parent node の1つのキー区間と関連する child pointer は実際には 2 つのノードを参照
  • half-split ノードに到達したら、search key が high fence key と比較され、fence key より多ければ right neighbor へ進む
• parent に high fence key を post するステップ
  • このステップが完了してなくてもデータ構造に不整合は発生しない
• Blink-tree の欠点
  • search の効率がやや落ちる
  • insert 率が高い時に 隣接ノード間で長い linked list ができないようにするソリューションが必要
  • tree の構造的一貫性の検証が複雑でおそらく効率が落ちること
• appropriate parent node によって point されるノードに対する split 操作を制限することで、長い linked list を防ぐことができる
  • [Jaluta et al. 2005] で詳細に述べられている

abst

• 新しい concurrent and recoverable B-link-tree algorithm を提案
• 常に B-link tree のバランスがメンテされる
• key-range locking によって Repeatable-read-level を保証
• WAL, steal and no-force policy
• leaf に対するレコードの insert and deletes は physiological redo-undo log record を記録
• page split or merge は latch を使って atomic に実行
  • 一度にたかだか2つの X-latch
  • 構造変化は1つの physiological redo-only log record を記録
  • →構造変化は undone されない

intro

B-link-tree は Lehman and Yao によって紹介

• tree traversal の間
  • search ではノードを lock しない
  • insert は一度に1つのノードを S-lock
    • child ノードの lock を獲得する前に parent ノードの lock を release
• insert は leaf ノードに達すると X-lock を取る
• split は2フェーズで実行
  • half-split → complete split
• 問題は merge に対する provision がないこと

Sagiv の B-link algorithm の実装

• search and insert 操作では同時に1つのみノードを lock
  • child ノードの lock を取る前に parent ノードの lock を release
• 主要な貢献は独立した compression プロセス
  • search and insert に並行して実行
• 欠点
  • どのくらいの頻度で compression するかが不明確
    • compression 前に B-link tree のバランスが崩れ、性能が悪くなる可能性がある
  • search で間違ったノードにたどり着く可能性がある
    • entries は右に寄せられたり、左に寄せられたりする
    • また inserters は右から離れたノードを更新しようとする可能性がある
      • ?
  • compression 時に隣接する2つのレベルの3つのノードを同時に X-lock

Lanin and Shasha の insertions と対称的な deletions の b-link-tree algorithm

• search and insert では Sagiv と同じ locking protocol を使用
• merge は2フェーズ
  • half-merge
    • 同時に同レベルの2つのノードを X-locks
  • complete-merge
    • 1つのノードを X-lock
• complete-split and complete-merge 操作は parent ノードの更新時に "inconsistent" な状況に遭遇する可能性がある
  • complete-split 時には parent ノードに対して insert しようとする key value がすでに parent に存在する可能性がある
  • complete-merge 時には parent ノードから delete しようとするkey がすでに存在しない可能性がある
• 欠点
  • complete-split or complete-merge は "inconsistent" な状況に遭遇したら tree を root から辿り直して実行する必要がある
  • parent に link されていない right sibling の長い chain を持つことになる可能性がある

B-link algorithm に関する主要な問題

1. Variable-length key は扱えない
2. B-link tree の parent ノード P の右端の子を削除する時に、P の high-key value が tree を伝搬(rootに向けて)
3. split 操作は split 対象のノードの X-lock を取り、新しくアロケートされるノードの X-lock は取らないが、トランザクションが key-range-scan をする際に安全ではない
4. split or merge はトランザクションの一部で、concurrency を制限
5. concurrency control は node level で、concurrency を制限
6. トランザクションは single operation のみを考慮、key-range scan は考慮されてない
7. 空のノードはすぐには deallocate できず、parent に link されていない right sibling ノードの chain は長くなりえ、パフォーマンスが落ちる
8. トランザクションの abort やシステム障害を処理する recovery protocol は規定されていない
9. 形式的証明がなく、worst-case の分析もされていない

Lomet and Salzberg algorithm がこの paper のものに近い

• tree のいくつかの level が関与する structure modification はより小さい structure modification(atomic action) に分けられる
• leaf level より上の level の structure modification は database transaction として独立
• separate database transaction: "nested top action"
• atomic structure modification は redo-undo log records を記録
• searchers, updaters は latch-coupling protocol を採用
  • S and U latches: U は S と互換だが他の U や X と非互換
    -page を更新する必要がある時、U latch は X latch に upgrade
• earlier B-link-tree algorithm の多くの問題を避けることができるが、まだ問題がある
  • key-range scan は含まれていない
  • split 対象のみ X-latch を取るが key-range-scan 時に安全ではない
  • merge or distribute には2つの隣接レベルに対する3つのX-latchが必要
  • TBD