入門 B-link tree
概要
DBMS で広く利用されている B+ tree には様々な variant が存在するが、B-link tree もその1つ。
シンプルなラッチプロトコルで並行アクセスをさばけるよう、リーフノード以外のノードにも右の隣接ノードへのポインタを持たせた構造となっており、PostgreSQL で使われていることでも有名。
この記事では主にこの B-link tree に焦点を当てる。
B+ tree 全般やその他インデックス技術自体に興味がある場合は「最強DB講義 #10 いまどきのデータベース索引技術(石川佳治 教授)」の講義資料を読むのがおすすめ。
B-link tree 理解する上で必須な知識「ラッチ」
「ラッチ」というのはいわゆるロックのことだが、DB においては「ロック」というとトランザクション分離のための高価な(数千CPUサイクルを要する)処理を指すことが多く、「ラッチ」というとメモリ上のデータ構造への並行アクセス時にデータ構造を保護する安価な(数十CPUサイクル程度の)処理を指すことが多い。
DBにおけるロックとラッチの使い分けについては以下のような整理がされている[1] 。
| ロック | ラッチ | |
|---|---|---|
| 分離対象 | トランザクション | スレッド |
| 保護対象 | データベースコンテンツ | In-memory データ構造 |
| 保持期間 | トランザクション全体 | クリティカルセクション |
| モード | shared, exclusive, update, intention, ... | read, write |
| Deadlockへの対応 | 検出して解消 | 回避 |
| ↑の方法 | 待ちグラフの分析, タイムアウト, ... | コーディングの規律 |
| 保持方法 | ロックマネージャーのハッシュテーブル | 保護されたデータ構造 |
B+ tree におけるラッチの必要性と課題
B+ tree では、リーフノードへキー追加時にノードの空きスペースが足りない場合、ノードをスプリットをしてスペースを確保する必要がある。またキーが削除されてノードがスカスカになった場合は逆にノードをマージしてスペースを節約する必要がある。
以下に、スプリット操作の例を挙げる。
1 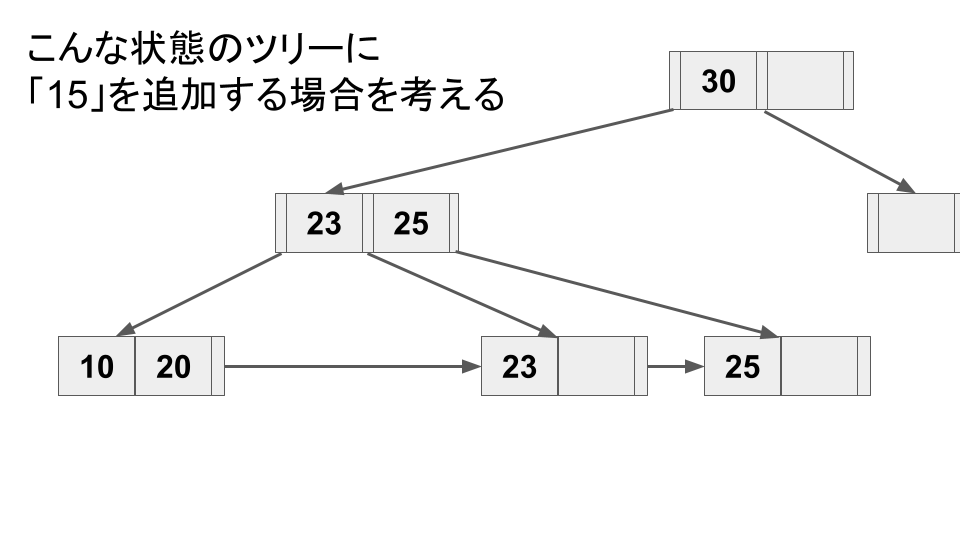
|
2 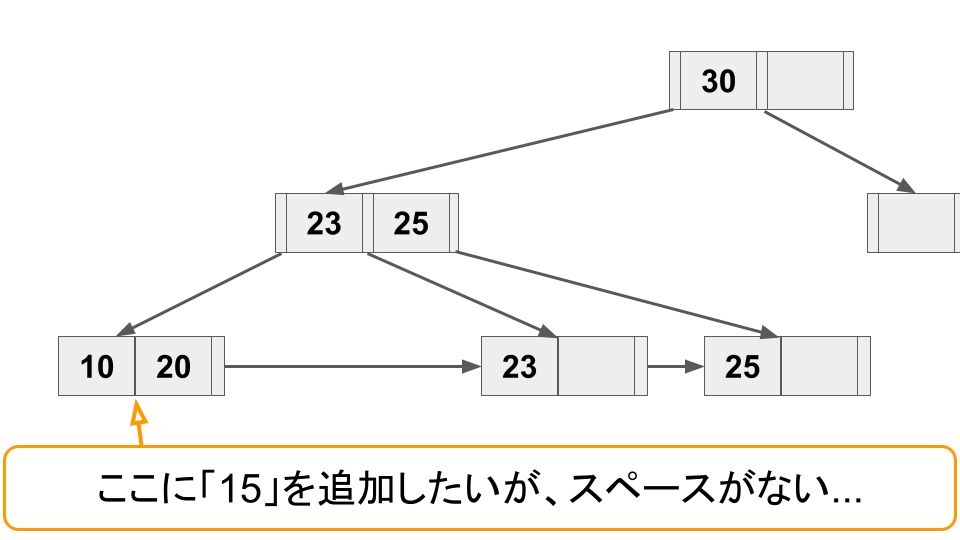
|
3 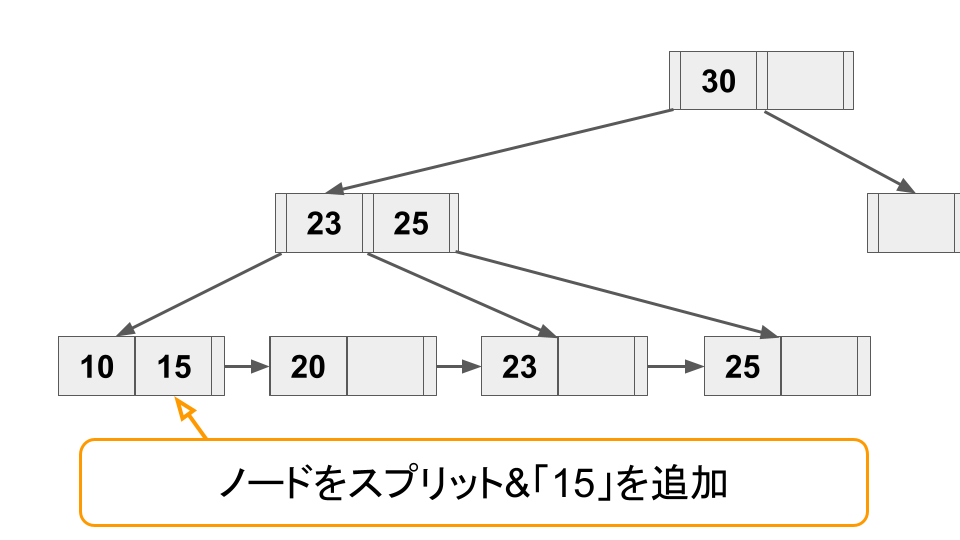
|
4 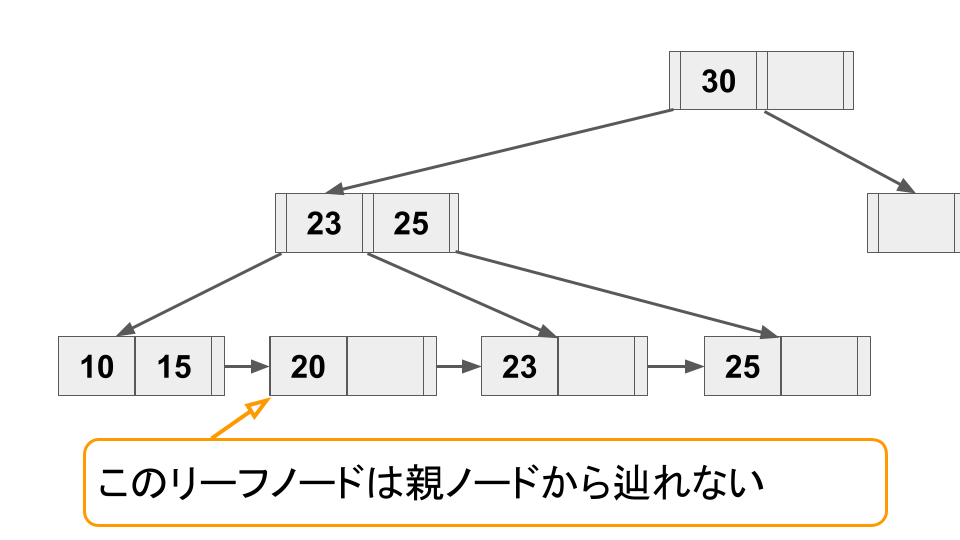
|
5 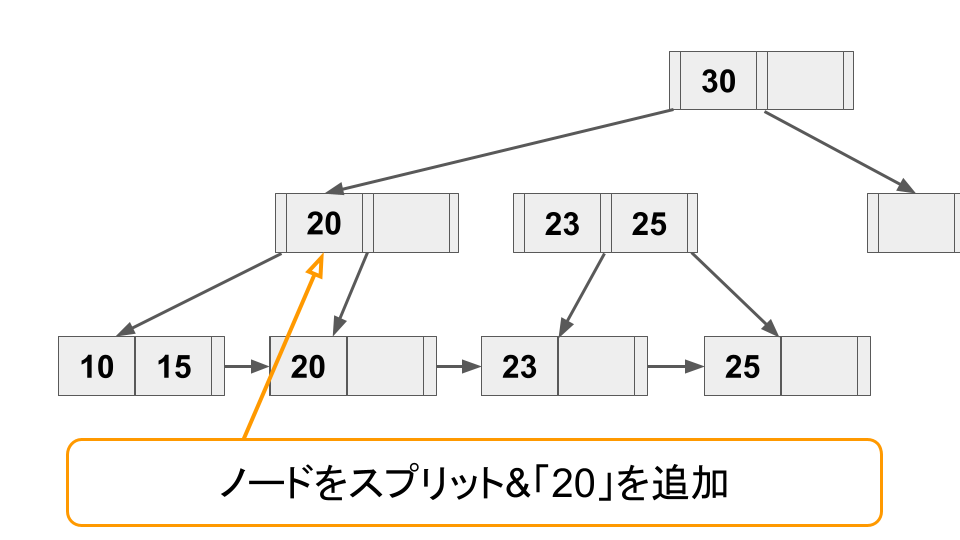
|
6 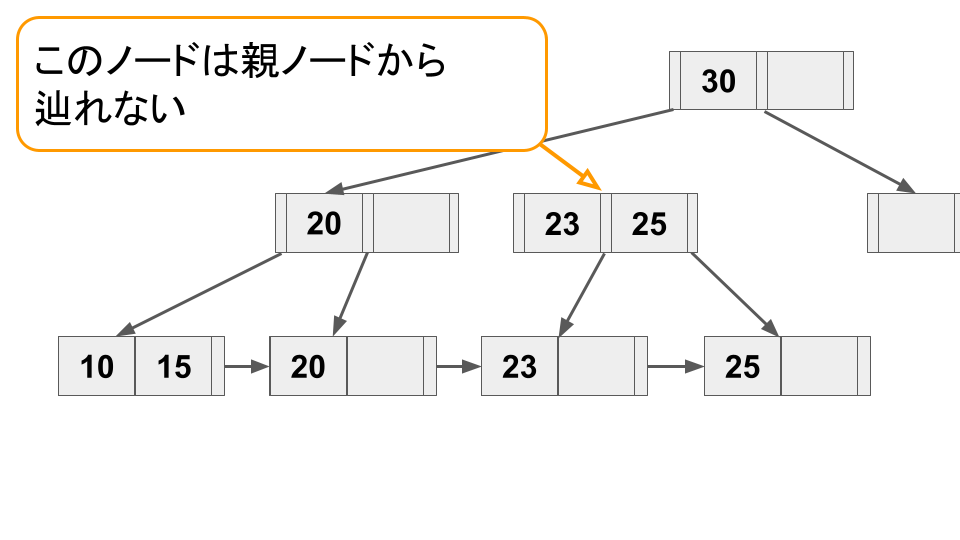
|
7 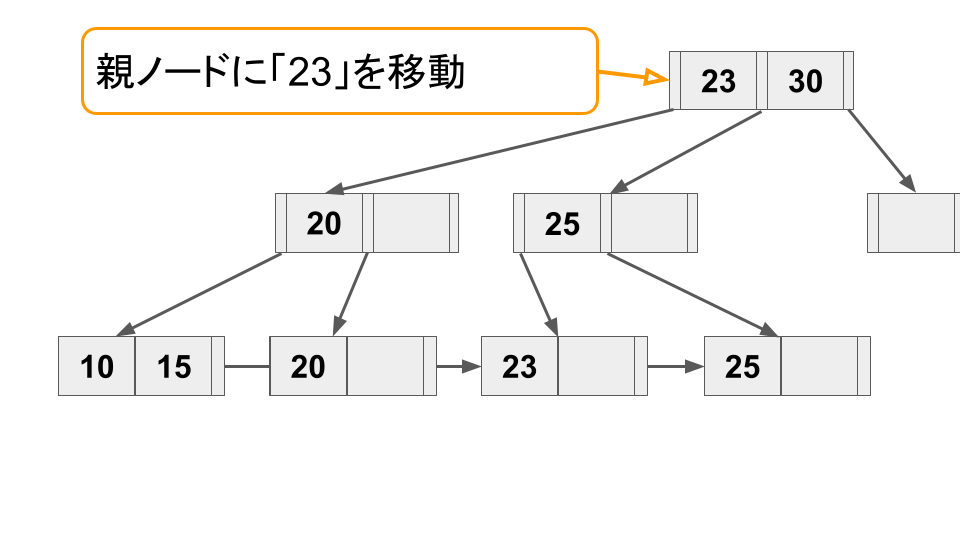
|
このようにノードのスプリット操作はリーフに留まらず親ノードに伝搬することがある(最悪ルートノードまで伝搬する可能性がある)。
B+ tree への値の追加アルゴリズムはこれでわかるB-treeアルゴリズム / B-tree algorithmが分かりやすいのでおすすめ。
さて、上記の例ではスプリット操作のみが実行されている状態だったが、並行して読み取り操作が行われると、以下のような状況が起こり得る。
1 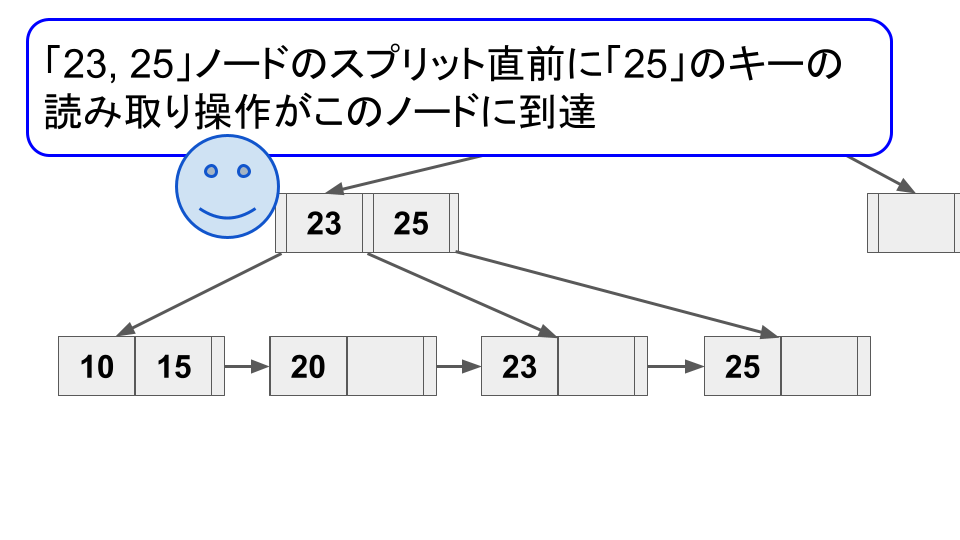
|
2 
|
3 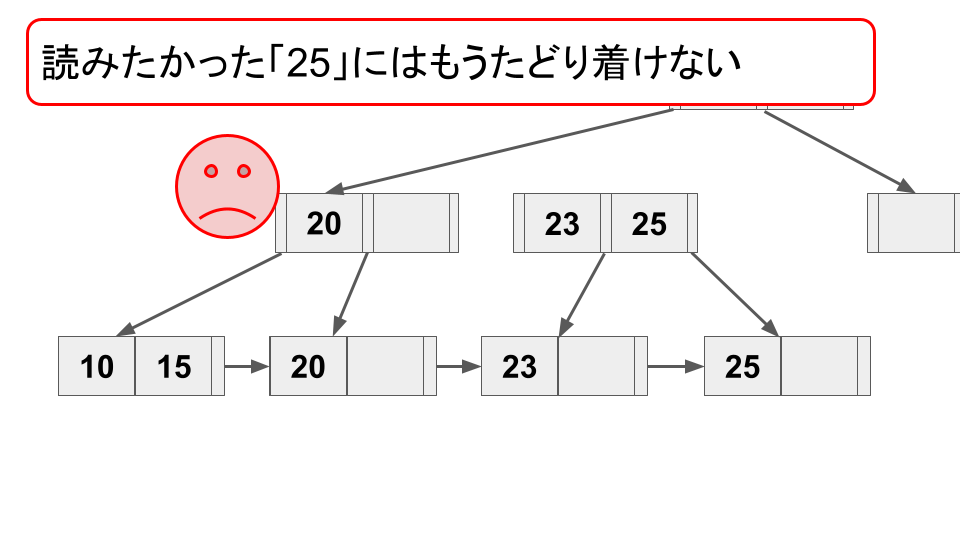
|
このような状況が起こった場合、読み取り操作は対象のキー(例では「25」)がツリーに無いと勘違いするか、もしくはおかしい状況に気づいたとしても再度ルートから読み取り操作をやり直す必要が出てくる。
そこで B+ tree のアルゴリズムでは、ルートからリーフへとツリーを辿る際に経路上の全ノードのラッチを獲得していくことで、並行アクセス時にツリーを保護する。
ただ、ツリー操作が終わるまでルートからリーフにかけてラッチを持ち続けていると並行性が損なわれるため、操作が安全に行えることが確認できたタイミングで不要なラッチを解放することが多い。
例えばキーの追加操作に伴ってルートからリーフを辿る場合、スプリットせずに挿入スペースが確保できるノードを見つけてラッチを獲得次第、そこまでの経路のノードに対するラッチは解放できる(スプリットが伝搬することがないため)。
この手の最適化を施したラッチプロトコルは、ラッチクラビングもしくはラッチカップリングと呼ばれる[2]。
CMUの講義のスライドに search, delete, insert 時のラッチの扱いについての説明があるが、見ると分かる通り最適化したラッチカップリングでも複数のツリーレベルのノードに渡るラッチの獲得が必要で、並行性を阻害してしまう。
それに対して B-link tree は同時獲得するラッチ数を減らすことができる。
B-link tree とは
B-link tree は Lehman & Yao によってEfficient locking for concurrent operations on B-treesにて提案された手法で、B+ tree と違いリーフノード以外のノードも右隣のノードへのポインタを持つ。
このポインタのお陰で、スプリット直後の新しいノードが親ノードと繋がっていなくても、辿れるようになる。
1 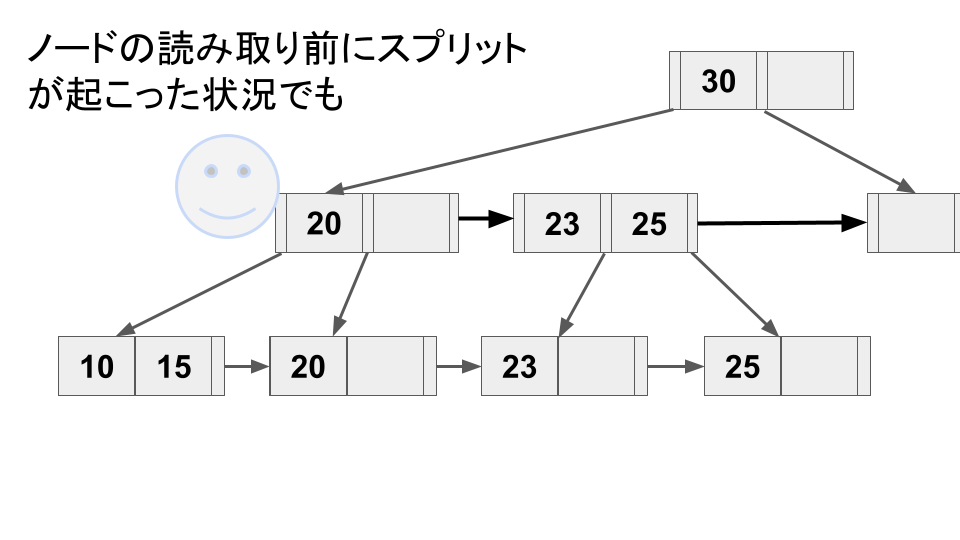
|
2 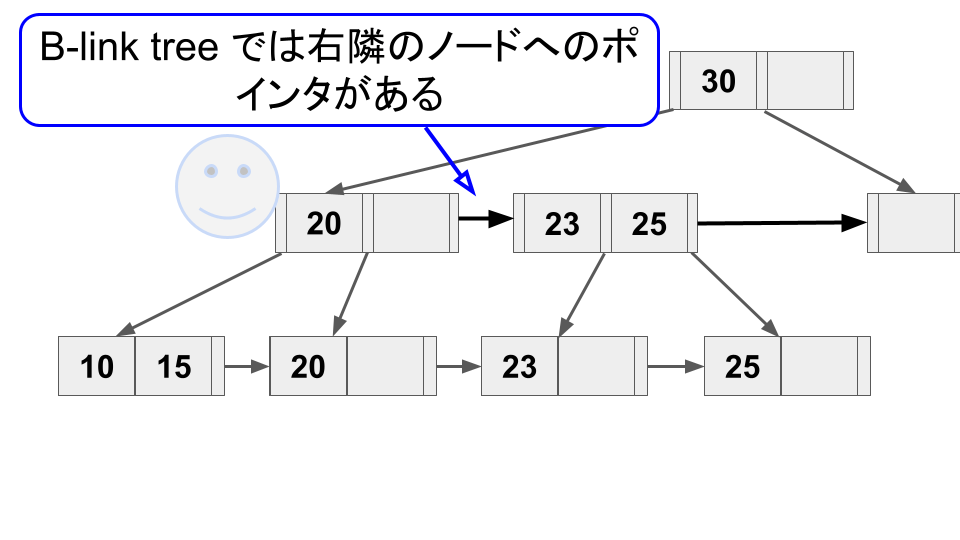
|
3 
|
このようにスプリット直後に親ノードとまだ繋がっていない状態は "half-split" と呼ばれ[3]、ツリー操作上は1つのノードとして扱うことができる。ただ、このままでは右ノードを辿るオーバーヘッドがあるので、なるべく速やかに親ノードと繋がった方がよい。
このように、スプリット中でも読み取りに支障が出ないことから、Lehman & Yao の論文では読み取り操作ではラッチ獲得不要で、更新操作では更新対象のノードに対してのみラッチを獲得すれば良く、同時ラッチ獲得数は最大でも3つと説明されている[4]。
ただし、読み取りや書き込みをアトミックに実行できることを仮定するのはあまり合理的ではなく、Lehman & Yao 以降の B-link tree 論文では素朴に shared と exclusive モードのラッチを採用していることが多い。
また、Lehman & Yao の提案手法ではノードのマージやリバランスについては考慮されておらず、この点も改良余地が残されている状態だった。
B-link tree の特徴として他にもハイキーなどがあるがここでは割愛。
ノードのマージも考慮された B-link tree アルゴリズム
1981 年に Lehman & Yao の論文が出た後、B-link tree の研究が進み、1986 年に Lanin & Shasha のA symmetric concurrent B-tree algorithmでノードのマージも考慮された手法が提案されている。
私がこの論文を知ったきっかけは PostgreSQL の README で、リンク先にあるように PostgreSQL では Lanin & Shasha の手法の simplified version を使っているらしい[5]。
Lanin & Shasha は、スプリットに対して対称性のあるマージ手法を提案している。
マージ操作を行う場合、マージされる側のノードに到達していた別の読み取り操作に影響が出てくることに対処する必要があるが、
1 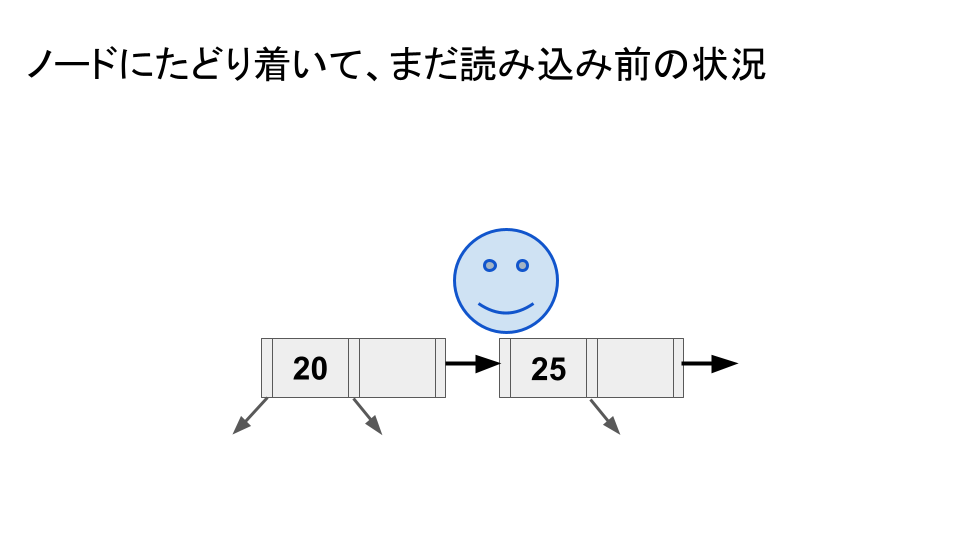
|
2 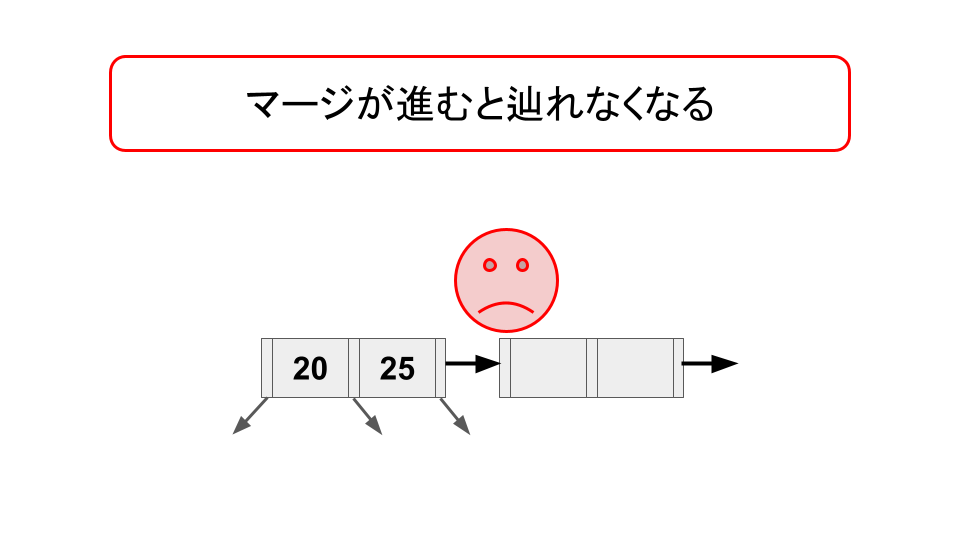
|
そこでマージされるノードからマージ先のノードへのポインタ(論文では outlink と呼んでいる)を持たせることで、マージが完了していない状態でも、別の読み取り操作を進行できるようにする。
1 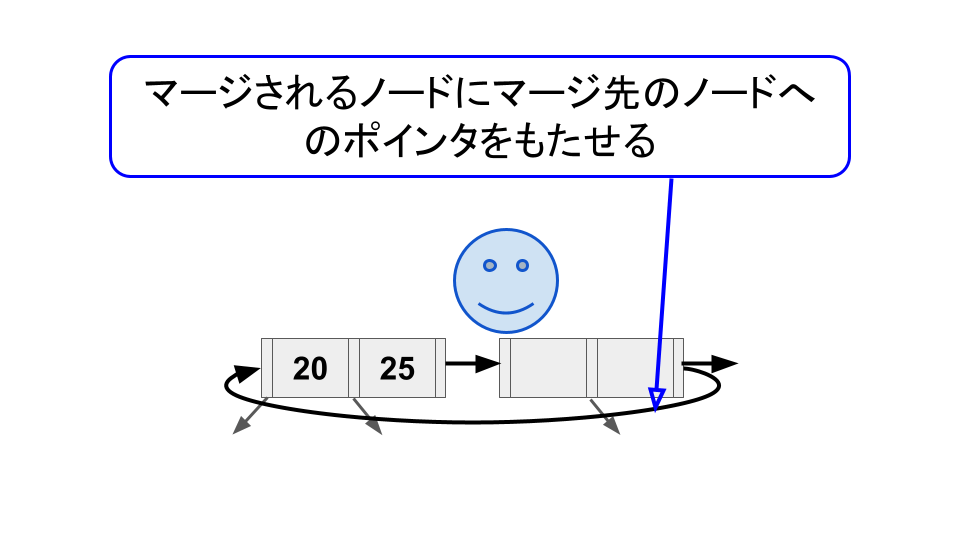
|
2 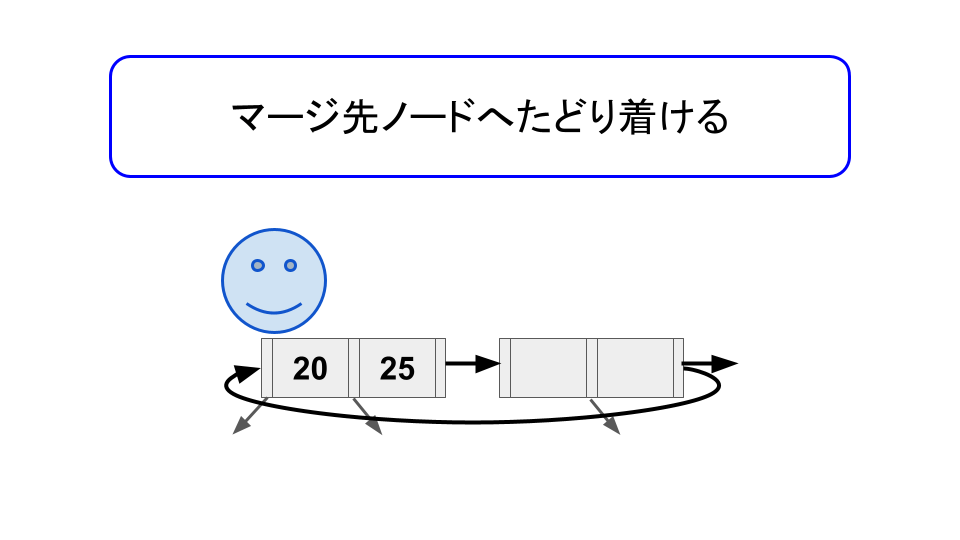
|
このマージが完了していないが他の操作を妨げない状態を "half-merge" と呼ぶ。"half-split" と対称性があり、分かりやすい。
論文ではこの他にもマージされたノードを deallocate する方法や、Lehman & Yao の手法よりもラッチの数を減らす工夫などが書かれている。
親と繋がっていない "half-split" 状態のノードチェーン問題
後続の研究で Lehman & Yao と Lanin & Shasha の手法の問題点(と改善点)が挙げられている。
その中でも、親ノードに繋がっていない "half-split" 状態のノードが長いチェーンを作ってしまう問題は深刻。
これは、"half-split" 状態のノードへのキーの追加と、親ノードとの接続操作が独立しているために起こりうるもので、場合によっては B tree 構造が崩れて単なる LinkedList 状態になってしまう。
この問題への対策が提案されている論文として Jaluta の Concurrency control and recovery for balanced Blink trees がある。
この論文は Graefe の A Survey of B-Tree Locking Techniques の B-link tree の節でも言及がされている。
Jaluta の手法では、"half-split" を発生させた操作では親ノードとの接続を行わず、後続の更新操作がルートからリーフに向けて辿る際に "half-split" 状態のノードを見つけたら順に直していき、バランスが取れたツリー構造を維持する、というもの。
直すのは "half-split" 状態だけでなく、キーが少なくなり過ぎているノードについてもマージやキーの再配置などで、アンバランスを是正する。
利用するラッチモードも shared, exclusive の他に update というものも導入しており、それなりにラッチカップリングを活用したアルゴリズムになっている。
Jaluta の論文は他にも key-range locking や recovery にも触れられていて、これまでに紹介した論文よりも広範なトピックを扱っている。
その他のB-link tree 関連のトピック
B-link tree 関連の論文としては、B-link tree に楽観的並行性制御を適用した OLFIT という手法や、メニーコア&フラッシュストレージへの最適化と B-link tree の要素を組み合わせた Foster B-treesや、ラッチフリーのアプローチと B-link tree の要素を取り入れた Bw-Tree などがある。
(あくまで私が把握している範囲のものなので、という話なので他にもあったらコメント下さい)
ただ、まだ読めていないので、リンクのみ紹介。
最後に
最近 B-link tree のソースを写経しており、その際に調べたことを軽くまとめ始めたら思いの外、時間を掛けてしまった。
ここまでまとめてみて、Lehman & Yao と Lanin & Shasha の手法をベースにした PostgreSQL は "half-split" 状態のノードチェーン問題にどう対処しているのか気になってきたので、そのうち調べてみようと思う。
-
語感的に、最適化せずに単にラッチを組み合わせる場合でも使って良さそうだが、詳説データベースには "ラッチが保持される時間を最小化すればよいのです。それを達成するために使用できる最適化の1つは、ラッチクラビングまたはラッチカップリングと呼ばれます" と記載があり、またCMUの講義のスライドにも "Acquire and release latches on B+Tree nodes when traversing the data structure." とある。 ↩︎
-
Lehman & Yao の最初の論文には出てこないので、後にそう呼ばれるようになった模様。 ↩︎
-
ノードのスプリットが起きた際、スリプット対象のノードに対するラッチを保持した状態で、親ノードのラッチも獲得して新しくキーを挿入しようとする。ただ、その間に親もスプリットされてキーの挿入先ノードとして不適切な状態になっている場合、親ノードの右隣のノードを辿りつつラッチを獲得する。元の親ノードのラッチはすぐに解放するものの、解放前は同時に3つのラッチを保持していることになる。 ↩︎
-
README の情報量は多く、Lehman & Yao や Lanin & Shasha をベースにしつつも、様々な改変が加えられていることが知れて面白い。 ↩︎
Discussion