Zenn
🌊

一様乱数から正規乱数を生成する方法【Python】

2023/10/15に公開
Python
乱数
tech

はじめに

この記事では、[0,1) の一様乱数から標準正規分布 \mathcal{N}(0,1) に従う正規乱数を生成する方法について説明し、Python で簡易的に実装します。また、正規乱数から多次元正規乱数を生成する方法についても取り扱います。

今回の元ネタは、参考文献でも挙げている伏見正則『乱数』です。これは日本語で書かれた数少ない乱数についての入門書で、長い間絶版になっていました。ところが、なんと先日ちくま学芸文庫で復刊したことでようやく手に入れることができました！　この本では、メルセンヌ・ツイスター以前の内容が取り扱われていて、悪戦苦闘している歴史がよくわかりました。

正規乱数

正規分布に従う正規乱数は、様々な言語のライブラリでサポートされています。たとえば、Python の NumPy では次のように書けます。

import numpy as np
import matplotlib.pyplot as plt

N = 10000
mu = 0 # 平均値
sigma = 1 # 標準偏差
X = np.random.normal(mu, sigma, size=N)
plt.hist(X, bins=100)
plt.show()

このように基本的には一撃で正規乱数を生成できますが、今回は [0,1) の一様乱数から標準正規分布 \mathcal{N}(0,1) に従う正規乱数をいくつかの方法で生成します。ここでは、一様乱数の生成に NumPy の random.rand() を使います。

import numpy as np
import matplotlib.pyplot as plt

N = 10000
X = np.random.rand(N)
plt.hist(X, bins=100)
plt.show()

極座標法（Box-Muller）

U_1, U_2 を一様乱数とします。

\begin{align*} X_1 &= \sqrt{-2 \log U_1} \cos (2 \pi U_2) \\ X_2 &= \sqrt{-2 \log U_1} \sin (2 \pi U_2) \end{align*}

とすると、X_1 と X_2 は互いに独立で、標準正規分布 \mathcal{N}(0,1) に従う乱数となります。

import numpy as np
import matplotlib.pyplot as plt

N = 10000
U1 = np.random.rand(N)
U2 = np.random.rand(N)
X1 = np.sqrt(-2*np.log(U1)) * np.cos(2*np.pi*U2)
X2 = np.sqrt(-2*np.log(U1)) * np.sin(2*np.pi*U2)

fig, ax = plt.subplots(1, 2, figsize=(9, 4))
ax[0].hist(X1, bins=100)
ax[1].hist(X2, bins=100)
ax[0].set_title("X1 Histogram")
ax[1].set_title("X2 Histogram")
plt.show()

極座標法（Marsaglia）

極座標法（Box-Muller）は比較的遅いので、\cos, \sin を計算しなくても済むように改良された方法が Marsaglia によって提案されました。

  1. 一様乱数 U_1, U_2 を発生し、V_1 \leftarrow 2U_1 - 1, V_2 \leftarrow 2U_2 - 1 とする。
  2. S \leftarrow V_1^2 + V_2^2.
  3. S \ge 1 なら 1. にもどる。
  4. X_1 \leftarrow V_1 \sqrt{\frac{-2\log S}{S}}, X_2 \leftarrow V_2 \sqrt{\frac{-2\log S}{S}}. 
import numpy as np
import matplotlib.pyplot as plt

def Marsaglia():
  while True:
    U1 = np.random.rand()
    U2 = np.random.rand()
    V1 = 2*U1 - 1
    V2 = 2*U2 - 1
    S = V1**2 + V2**2
    if S < 1:
      break
  X1 = V1 * np.sqrt(-2*np.log(S)/S)
  X2 = V2 * np.sqrt(-2*np.log(S)/S)
  return X1, X2

N = 10000
X = np.array([Marsaglia() for _ in range(N)])
X1 = X[:,0]
X2 = X[:,1]

fig, ax = plt.subplots(1, 2, figsize=(9, 4))
ax[0].hist(X1, bins=100)
ax[1].hist(X2, bins=100)
ax[0].set_title("X1 Histogram")
ax[1].set_title("X2 Histogram")
plt.show()

中心極限定理の応用

U_1, U_2, \dots, U_n を一様乱数とします。

X = \left( U_1 + U_2 + \cdots + U_n - \frac{n}{2} \right) \left/ \sqrt{\frac{n}{12}} \right.

n = 12 がよく使われます。しかし、速度は他に比べるとかなり遅いです。

import numpy as np
import matplotlib.pyplot as plt

def CLT_application(n=12):
  U = np.random.rand(n)
  return (np.sum(U) - n/2) / np.sqrt(n/12)

N = 10000
X = np.array([CLT_application() for _ in range(N)])
plt.hist(X, bins=100)
plt.show()

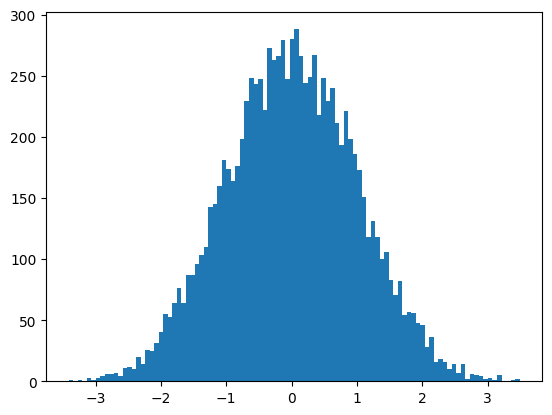
棄却法による正の正規乱数の生成

指数乱数

逆関数法を使うと、平均 \mu の指数分布に従う乱数は以下の式で生成できます。ここで、U は一様乱数とします。ただし、U=0 とならないように注意する必要があります。

X = -\mu \log U

正の正規乱数

  1. 平均が 1 の指数乱数 V_1, V_2 を発生する。
  2. V_2 < (V_1 - 1)^2 / 2 なら 1. にもどる。
  3. X \leftarrow V_1.
import numpy as np
import matplotlib.pyplot as plt

def exp_dist(mu=1):
  while True:
    U = np.random.rand()
    if (U != 0):
      break
  return -mu * np.log(U)

def reject_law():
  while True:
    V1 = exp_dist()
    V2 = exp_dist()
    if V2 >= (V1-1)**2 / 2:
      break
  return V1

N = 10000
X = np.array([reject_law() for _ in range(N)])
plt.hist(X, bins=100)
plt.show()

一様乱数の比

  1. 一様乱数 U_1, U_2 を発生し、X \leftarrow \sqrt{8/e}\left(U_2 - \frac{1}{2}\right) / U_1 とする。
  2. X^2 \le 5 - 4 e^{1/4} U_1 なら X を採用して終わり。
  3. X^2 \ge 4e^{-1.35}/U_1+1.4 なら 1. にもどる。
  4. X^2 \le -4 \log U_1 なら X を採用して終わり。そうでなければ 1. にもどる。
import numpy as np
import matplotlib.pyplot as plt

def ratio_based():
  while True:
    U1 = np.random.rand()
    U2 = np.random.rand()
    X = np.sqrt(8/np.e) * (U2 - 0.5) / U1
    if X**2 <= 5 - 4*np.exp(0.25)*U1:
      break
    if X**2 >= 4*np.exp(-1.35)/U1 + 1.4:
      continue
    if X**2 <= -4*np.log(U1):
      break
  return X

N = 10000
X = np.array([ratio_based() for _ in range(N)])
plt.hist(X, bins=100)
plt.show()

速度の検証（要検討）

各種正規乱数の生成速度を比較してみました。実行環境は Google Colab です。とはいえ、速度が出るようなプログラムの書き方をしていないので、あまり意味のある検証ではありませんが…

計算プログラム
import time
import numpy as np

N = 1000000
num_iterations = 10
print(f"N = {N}")
print(f"num_iterations = {num_iterations}")

def measure_random_generation_speed(random_generator, size=N):
    start_time = time.time()

    _ = random_generator(size=size)

    end_time = time.time()
    elapsed_time = end_time - start_time
    return elapsed_time

def box_muller(size):
  U1 = np.random.rand(N//2)
  U2 = np.random.rand(N//2)
  X1 = np.sqrt(-2*np.log(U1)) * np.cos(2*np.pi*U2)
  X2 = np.sqrt(-2*np.log(U1)) * np.sin(2*np.pi*U2)
  return (X1, X2)

def Marsaglia():
  while True:
    U1 = np.random.rand()
    U2 = np.random.rand()
    V1 = 2*U1 - 1
    V2 = 2*U2 - 1
    S = V1**2 + V2**2
    if S < 1:
      break
  X1 = V1 * np.sqrt(-2*np.log(S)/S)
  X2 = V2 * np.sqrt(-2*np.log(S)/S)
  return X1, X2

def Marsaglia_N(size):
  X = np.array([Marsaglia() for _ in range(size//2)])
  X1 = X[:,0]
  X2 = X[:,1]
  return (X1, X2)

def CLT_application(n=12):
  U = np.random.rand(n)
  return (np.sum(U) - n/2) / np.sqrt(n/12)

def CLT_application_N(size):
  X = np.array([CLT_application() for _ in range(size)])
  return X

def exp_dist(mu=1):
  while True:
    U = np.random.rand()
    if (U != 0):
      break
  return -mu * np.log(U)

def reject_law():
  while True:
    V1 = exp_dist()
    V2 = exp_dist()
    if V2 >= (V1-1)**2 / 2:
      break
  return V1

def reject_law_N(size):
  X = np.array([reject_law() for _ in range(size)])
  return X

def ratio_based():
  while True:
    U1 = np.random.rand()
    U2 = np.random.rand()
    X = np.sqrt(8/np.e) * (U2 - 0.5) / U1
    if X**2 <= 5 - 4*np.exp(0.25)*U1:
      break
    if X**2 >= 4*np.exp(-1.35)/U1 + 1.4:
      continue
    if X**2 <= -4*np.log(U1):
      break
  return X

def ratio_based_N(size):
  X = np.array([ratio_based() for _ in range(N)])
  return X

# NumPy
total_time = 0
for _ in range(num_iterations):
    elapsed_time = measure_random_generation_speed(np.random.normal)
    total_time += elapsed_time
average_time = total_time / num_iterations
print(f"平均実行時間（NumPy）: {average_time:.6f} 秒")

# Box-Muller
total_time = 0
for _ in range(num_iterations):
    elapsed_time = measure_random_generation_speed(box_muller)
    total_time += elapsed_time
average_time = total_time / num_iterations
print(f"平均実行時間（Box-Muller）: {average_time:.6f} 秒")

# Marsaglia
total_time = 0
for _ in range(num_iterations):
    elapsed_time = measure_random_generation_speed(Marsaglia_N)
    total_time += elapsed_time
average_time = total_time / num_iterations
print(f"平均実行時間（Marsaglia）: {average_time:.6f} 秒")

# CLT
total_time = 0
for _ in range(num_iterations):
    elapsed_time = measure_random_generation_speed(CLT_application_N)
    total_time += elapsed_time
average_time = total_time / num_iterations
print(f"平均実行時間（CLT）: {average_time:.6f} 秒")

# reject law
total_time = 0
for _ in range(num_iterations):
    elapsed_time = measure_random_generation_speed(reject_law_N)
    total_time += elapsed_time
average_time = total_time / num_iterations
print(f"平均実行時間（reject law）: {average_time:.6f} 秒")

# ratio based
total_time = 0
for _ in range(num_iterations):
    elapsed_time = measure_random_generation_speed(ratio_based_N)
    total_time += elapsed_time
average_time = total_time / num_iterations
print(f"平均実行時間（ratio based）: {average_time:.6f} 秒")

N = 1000000
num_iterations = 10
平均実行時間（NumPy）: 0.038441 秒
平均実行時間（Box-Muller）: 0.046128 秒
平均実行時間（Marsaglia）: 2.479360 秒
平均実行時間（CLT）: 6.040100 秒
平均実行時間（reject law）: 3.882312 秒
平均実行時間（ratio based）: 4.628818 秒

当たり前ですが、NumPy の random.normal() が最も速い結果となりました。次点が Box-Muller ですが、これは for を使わずに NumPy の機能で作成したからだと考えられます。他の順番は順当でしょう。やはり、中心極限定理を使った方法が一番遅くなっています。

多次元正規乱数

標準正規分布 \mathcal{N}(0,1) に従う正規乱数を使って、多変量正規分布 \mathcal{N}(\mathbf{0}, \mathbf{\Sigma}) に従う多次元正規乱数を生成します。ちなみに、NumPy では random.multivariate_normal()、SciPy では stats.multivariate_normal() で生成できます。このプログラムでは \mathbf{\Sigma} = \mathbf{I} としました。

import numpy as np
from scipy.stats import multivariate_normal

N = 100000
mu = np.array([0, 0])
sigma = np.array([[1,0],[0,1]])

X1 = np.random.multivariate_normal(mu, sigma, size=N)
X2 = multivariate_normal(mu, sigma).rvs(size=N)

fig, ax = plt.subplots(1, 2, figsize=(9, 4))
ax[0].hist2d(X1[:,0], X1[:,1], bins=100, cmap="inferno")
ax[1].hist2d(X2[:,0], X2[:,1], bins=100, cmap="inferno")
ax[0].set_title("NumPy")
ax[1].set_title("SciPy")
plt.show()

まず、共分散行列 \mathbf{\Sigma} をコレスキー分解します。

\mathbf{\Sigma} = \mathbf{L}\mathbf{L}^T

コレスキー分解とは、下三角行列 \mathbf{L} に分解する方法です。次に、x_i \,(i=1,2,\dots,n) を正規乱数とし、\mathbf{x} = (x_1, x_2, \dots, x_n)^T とおきます。このとき、\mathbf{L}\mathbf{x} の分布は \mathcal{N}(\mathbf{0}, \mathbf{\Sigma}) となります。

from scipy import linalg

sigma = np.array([[1,0],[0,1]])
L = linalg.cholesky(sigma)

def normal_dist_2(L):
  x = np.array([np.random.normal() for _ in range(2)])
  return L@x

N = 100000
X = np.array([normal_dist_2(L) for _ in range(N)])
plt.hist2d(X[:,0], X[:,1], bins=100, cmap="inferno")
plt.colorbar()
plt.show()
\mathbf{\Sigma} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}

\mathbf{\Sigma} = \begin{bmatrix} 1 & 0.9 \\ 0.9 & 1 \end{bmatrix}

\mathbf{\Sigma} = \begin{bmatrix} 1 & -0.7 \\ -0.7 & 1 \end{bmatrix}

おわりに

今回は、ブラックボックスとなりがちな正規乱数の生成方法について説明しました。基本的には一様乱数を変換することで欲しい分布の乱数を生成することができます。その方法だけでも色々提案されており、ここでは紹介していないような複雑なものもあります[1]。乱数って沼ですね。

参考文献

今回の元ネタは 1. です。特に正規乱数の節は大体一緒なので、詳細はそちらを参照してください（一部数式に誤植があるので注意してください）。多変量については 2. を参考にしました。1. でも触れられていますが、2. のほうがわかりやすいです。

  1. 伏見正則 (2023). 『乱数』. 筑摩書房.
  2. 持橋大地, 大羽成征 (2019). 『ガウス過程と機械学習』. 講談社.
脚注

  1. たとえば、Ziggurat 法とか。メモリ領域をほかのアルゴリズムより大きく使う代わりに高速な生成法。 ↩︎

GitHubで編集を提案

Discussion