Zenn
📘

【力学系超入門】平衡点の分岐：線形安定性解析【Python】

2024/06/18に公開
Python
力学系
tech

1. 力学系

力学系とは

力学系（Dynamical System）は、時間ともに動的に変化するシステムを意味する。力学系の目的は、システムの状態がどのように時間発展するかを理解し、そのパターンや特性を解析することである。

例えば、これまで以下のような分野で応用されてきた。

  • 物理学：天体力学
  • 工学：制御理論、電気回路
  • 生物学：生態系のモデリング
  • 経済学：市場のダイナミクス

上記の内容を見てわかる通り、力学系は連続時間の微分方程式と離散時間の差分方程式で数理モデル化されたシステムについて取り扱う。

この記事では力学系の分岐について説明する。元ネタは小室元政『新版 基礎からの力学系 分岐解析からカオス的遍歴へ』である。というか、この本を勉強しているときのノートを抜粋＆整理したのがこの記事である（そのため、基本的な流れや記述が大きく類似している）。この本では古いC++のソフトでプログラム記述されているので、それをPythonで改めて書こうというのが実はそもそものモチベーションであったが、気が付いたらかなりのボリュームになってしまった。

Python環境について

バージョン：3.12.3

$ pip install setuptools
$ pip install numpy
$ pip install scipy
$ pip install matplotlib
$ pip install japanize-matplotlib

単振り子

簡単な力学系の例として単振り子を紹介し、力学系の基本的な概念を導入する。

まず摩擦や空気抵抗を無視した場合、単振り子の微分方程式は次の通りである。ただし、\dot{}=\frac{d}{dt} である。

\begin{equation*} \begin{cases} \dot{\theta} = \omega \\ \dot{\omega} = -\frac{g}{l} \sin\theta \end{cases} \end{equation*}

(\theta, \omega)-平面（相空間）を考え、各点 (\theta,\omega) にベクトル

\left(\dot{\theta}, \dot{\omega}\right) = \left( \omega, -\frac{g}{l} \sin\theta \right)

を対応させる。この写像をベクトル場という。

g/l=1 として、このベクトル場をPythonで描画すると以下の通りである。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

gL = 1.0

theta_values = np.linspace(-2 * np.pi, 2 * np.pi, 20)
omega_values = np.linspace(-5, 5, 20)

theta, omega = np.meshgrid(theta_values, omega_values)

dtheta_dt = omega
domega_dt = -gL * np.sin(theta)

plt.figure(figsize=(10, 6))
plt.quiver(theta, omega, dtheta_dt, domega_dt, color="r")
plt.xlabel(r"$\theta$", fontsize=16)
plt.ylabel(r"$\omega$", fontsize=16)
plt.title("単振り子のベクトル場", fontsize=19)
plt.grid(True)
plt.show()

図を見易くするために、各ベクトルをすべて同じ長さにすることもある。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

gL = 1.0

theta_values = np.linspace(-2 * np.pi, 2 * np.pi, 20)
omega_values = np.linspace(-5, 5, 20)

theta, omega = np.meshgrid(theta_values, omega_values)

dtheta_dt = omega
domega_dt = -gL * np.sin(theta)

magnitude = np.sqrt(dtheta_dt**2 + domega_dt**2)
dtheta_dt_normalized = dtheta_dt / magnitude
domega_dt_normalized = domega_dt / magnitude

plt.figure(figsize=(10, 6))
plt.quiver(
    theta, omega, dtheta_dt_normalized, domega_dt_normalized, color="r", scale=40
)
plt.xlabel(r"$\theta$", fontsize=16)
plt.ylabel(r"$\omega$", fontsize=16)
plt.title("単振り子のベクトル場", fontsize=19)
plt.grid(True)
plt.show()

微分方程式の解曲線を、時間の向きも考慮して 軌道 (orbit) と呼ぶ。平面上に初期値をたくさん取って計算することで、流れ (flow) を描ける。これをPythonで描くと次の通りである。\theta, \omega が原点に近いところでは楕円形になっていて、周期的に振動していることが見て取れる。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy.integrate import solve_ivp


def pendulum(t, y):
    gL = 1.0
    theta, omega = y
    dydt = [omega, -gL * np.sin(theta)]
    return dydt


t_span = (0, 100)
t_eval = np.linspace(t_span[0], t_span[1], 1000)

# 初期値
np.random.seed(28)
num_initial_conditions = 200
initial_conditions_list = np.random.uniform(-5, 5, (num_initial_conditions, 2))


plt.figure(figsize=(10, 6))

for initial_conditions in initial_conditions_list:
    sol = solve_ivp(pendulum, t_span, initial_conditions, t_eval=t_eval)
    plt.plot(
        sol.y[0],
        sol.y[1],
    )

plt.grid(True)
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.xlabel(r"$\theta$", fontsize=16)
plt.ylabel(r"$\omega$", fontsize=16)
plt.title("単振り子の流れ", fontsize=19)
plt.grid(True)
plt.show()

質点の速さ l\dot{\theta} に比例した抵抗力（粘性抵抗）を追加する（c：比例定数）。

\begin{equation*} \begin{cases} \dot{\theta} = \omega \\ \dot{\omega} = -\frac{g}{l} \sin\theta - \frac{c}{m} \omega \end{cases} \end{equation*}

g/l=1, c/m=1 として、同様にベクトル場と流れをPythonで描画した。挙動は抵抗力なしと比べると変化していることが一発でわかる。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

gL = 1.0
cm = 0.5

theta_values = np.linspace(-2 * np.pi, 2 * np.pi, 20)
omega_values = np.linspace(-5, 5, 20)

theta, omega = np.meshgrid(theta_values, omega_values)

dtheta_dt = omega
domega_dt = -gL * np.sin(theta) - cm * omega

magnitude = np.sqrt(dtheta_dt**2 + domega_dt**2)
dtheta_dt_normalized = dtheta_dt / magnitude
domega_dt_normalized = domega_dt / magnitude

plt.figure(figsize=(10, 6))
plt.quiver(
    theta, omega, dtheta_dt_normalized, domega_dt_normalized, color="r", scale=40
)
plt.xlabel(r"$\theta$", fontsize=16)
plt.ylabel(r"$\omega$", fontsize=16)
plt.title("単振り子のベクトル場（粘性抵抗）", fontsize=19)
plt.grid(True)
plt.show()

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy.integrate import solve_ivp


def pendulum(t, y):
    gL = 1.0
    cm = 0.5
    theta, omega = y
    dydt = [omega, -gL * np.sin(theta) - cm * omega]
    return dydt


t_span = (0, 100)
t_eval = np.linspace(t_span[0], t_span[1], 1000)

# 初期値
np.random.seed(28)
num_initial_conditions = 100
initial_conditions_list = np.random.uniform(-4, 4, (num_initial_conditions, 2))


plt.figure(figsize=(10, 6))

for initial_conditions in initial_conditions_list:
    sol = solve_ivp(pendulum, t_span, initial_conditions, t_eval=t_eval)
    plt.plot(
        sol.y[0],
        sol.y[1],
    )

plt.grid(True)
plt.xlabel(r"$\theta$", fontsize=16)
plt.ylabel(r"$\omega$", fontsize=16)
plt.title("単振り子の流れ（粘性抵抗）", fontsize=19)
plt.grid(True)
plt.show()


次は振り子の台が x 方向に x_1 = B \sin \Omega t で振動しているとする。つまり、位置ベクトル \vec{r} は次のようになる。

\vec{r} = (l \sin \theta + B \sin \Omega t, -l \sin \theta)

このとき、運動方程式から微分方程式は以下の通りである。

\begin{equation*} \begin{cases} \dot{\theta} = \omega \\ \dot{\omega} = -\frac{g}{l} \sin\theta - \frac{c}{m} \omega + \frac{B\Omega^2}{l} \sin \Omega t \cos \theta \end{cases} \end{equation*}

このように右辺に時間 t を陽に含んでいる微分方程式を非自律系という。また、時間 t を陽に含んでいない微分方程式を自律系という。非自律系に対しては、(t,\theta,\omega)-空間（拡大相空間）を考え、空間の各点 (t,\theta,\omega) にベクトル

\left(1, \dot{\theta}, \dot{\omega} \right) = \left( 1, \omega, -\frac{g}{l} \sin\theta - \frac{c}{m} \omega + \frac{B\Omega^2}{l} \sin \Omega t \right)

を対応させる写像を考える。これを拡大相空間におけるベクトル場といい、同様に流れも定まる。

g/l=1.0, c/m=0.3, B/l=1.1, \Omega=1.0 としたときの軌道を計算する。初期値は (t,\theta,\omega)=(0,0,0) である。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp


def pendulum(t, y):
    gL = 1.0
    cm = 0.3
    Omega = 1.0
    Bl = 1.1
    theta, omega = y
    dydt = [
        omega,
        -gL * np.sin(theta)
        - cm * omega
        + (Bl * Omega**2) * np.sin(Omega * t) * np.cos(theta),
    ]
    return dydt


t_span = (0, 200)
t_eval = np.linspace(t_span[0], t_span[1], 10000)

initial_conditions = [0.0, 0.0]

sol = solve_ivp(
    pendulum,
    t_span,
    initial_conditions,
    t_eval=t_eval,
)

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection="3d")

ax.plot(sol.t[:3000], sol.y[0][:3000], sol.y[1][:3000])

ax.set_xlabel("t", fontsize=16)
ax.set_ylabel(r"$\theta$", fontsize=16)
ax.set_zlabel(r"$\omega$", fontsize=16)
plt.show()

十分時間が経過したあとの軌道を (\theta,\omega)-平面に射影する。軌道は1回巻きの楕円上を回る周回軌道に収束していることが見て取れる。

pythonプログラム
plt.figure(figsize=(10, 6))
plt.plot(sol.y[0][5000:], sol.y[1][5000:])
plt.xlabel(r"$\theta$", fontsize=16)
plt.ylabel(r"$\omega$", fontsize=16)
plt.title(r"$B/l = 1.1$", fontsize=19)
plt.grid(True)

plt.show()

B/l=1.42 としたときの軌道を計算する。さきほどと変わって、2回巻きの楕円上を回る周回軌道に収束している。なお、何かしらのパラメータを変更すると、もちろん軌道が収束するまでの時間や必要な精度が大きく変わってくるため、必要に応じてさきほどのような3次元プロットを見ながら射影すると便利である。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp


def pendulum(t, y):
    gL = 1.0
    cm = 0.3
    Omega = 1.0
    Bl = 1.42
    theta, omega = y
    dydt = [
        omega,
        -gL * np.sin(theta)
        - cm * omega
        + (Bl * Omega**2) * np.sin(Omega * t) * np.cos(theta),
    ]
    return dydt


t_span = (0, 1000)
t_eval = np.linspace(t_span[0], t_span[1], 500000)

initial_conditions = [0.0, 0.0]

sol = solve_ivp(
    pendulum,
    t_span,
    initial_conditions,
    t_eval=t_eval,
)

plt.figure(figsize=(10, 6))
plt.plot(sol.y[0][-10000:], sol.y[1][-10000:])
plt.xlabel(r"$\theta$", fontsize=16)
plt.ylabel(r"$\omega$", fontsize=16)
plt.title(r"$B/l = 1.42$", fontsize=19)
plt.grid(True)

plt.show()

さらに B/l=1.443 で計算すると、非周期軌道となる。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp


def pendulum(t, y):
    gL = 1.0
    cm = 0.3
    Omega = 1.0
    Bl = 1.443
    theta, omega = y
    dydt = [
        omega,
        -gL * np.sin(theta)
        - cm * omega
        + (Bl * Omega**2) * np.sin(Omega * t) * np.cos(theta),
    ]
    return dydt


t_span = (0, 1000)
t_eval = np.linspace(t_span[0], t_span[1], 500000)

initial_conditions = [0.0, 0.0]

sol = solve_ivp(
    pendulum,
    t_span,
    initial_conditions,
    t_eval=t_eval,
)

plt.figure(figsize=(10, 6))
plt.plot(sol.y[0][-40000:], sol.y[1][-40000:])
plt.xlabel(r"$\theta$", fontsize=16)
plt.ylabel(r"$\omega$", fontsize=16)
plt.title(r"$B/l = 1.443$", fontsize=19)
plt.grid(True)

plt.show()

このように、パラメータの変化にともない、システムが質的に変化することを分岐という。力学系では分岐の振る舞いを調べることが重要なテーマの1つである。

2. 線形ベクトル場

力学系では主に非線形力学系を対象とする。非線形力学系を解析するとき、線形力学系に近似することで線形代数の強力な恩恵を受けられることが多い。そこで、ここでは線形ベクトル場の性質について紹介する。

一般に線形ベクトル場は次のように定義される。

A を n 次正方行列とする。

\dot{\vec{x}} = A \vec{x}, \quad \vec{x} \in \mathbb{R}^n

で定義される \mathbb{R}^n 上のベクトル場を線形ベクトル場という。

1次元線形ベクトル場

1次元線形ベクトル場は、a を実定数として

\dot{x} = ax, \quad x \in \mathbb{R}

で定義される。t=0 のとき、x=x_0 を通る軌道は

x(t) = e^{at}x_0

である。定数 a の符号によってベクトル場の様子が変化する。

  • a>0：原点 O 以外の点は時間発展とともに原点から遠ざかる。
  • a=0：すべての点が不動。
  • a<0：原点 O 以外のすべての点は時間発展とともに原点に限りなく近づく。

見方を変えると、定数 a は 1\times1 行列でその固有値と考えられる。つまり、線形ベクトル場の挙動は固有値の符号が重要になることが予想できる。

各パターンにおけるPythonでの描画は以下の通りである。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(-2, 2, 400)

initial_conditions = [
    0.5,
    1.0,
    1.5,
    2.0,
    0.0,
    -0.5,
    -1.0,
    -1.5,
    -2.0,
]

plt.figure(figsize=(6, 6))

for x0 in initial_conditions:
    x_t = x0 * np.exp(t)
    (line,) = plt.plot(t, x_t)
    color = line.get_color()
    for i in range(0, len(t) - 1, 50):
        plt.arrow(
            t[i],
            x_t[i],
            t[i + 1] - t[i],
            x_t[i + 1] - x_t[i],
            shape="full",
            lw=0,
            length_includes_head=True,
            head_width=0.1,
            color=color,
        )


plt.title(r"$x(t) = e^t x_0$", fontsize=19)
plt.xlabel("t", fontsize=16)
plt.ylabel("x", fontsize=16)
plt.grid(True)

plt.xlim(-2, 2)
plt.ylim(-2, 2)

plt.show()

import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(-2, 2, 400)

initial_conditions = [
    0.5,
    1.0,
    1.5,
    0.0,
    -0.5,
    -1.0,
    -1.5,
]

plt.figure(figsize=(6, 6))

for x0 in initial_conditions:
    x_t = [x0 for _ in range(len(t))]
    (line,) = plt.plot(t, x_t)
    color = line.get_color()
    for i in range(0, len(t) - 1, 50):
        plt.arrow(
            t[i],
            x_t[i],
            t[i + 1] - t[i],
            x_t[i + 1] - x_t[i],
            shape="full",
            lw=0,
            length_includes_head=True,
            head_width=0.1,
            color=color,
        )


plt.title(r"$x(t) = x_0$", fontsize=19)
plt.xlabel("t", fontsize=16)
plt.ylabel("x", fontsize=16)
plt.grid(True)

plt.xlim(-2, 2)
plt.ylim(-2, 2)

plt.show()

import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(-2, 2, 400)

initial_conditions = [
    0.5,
    1.0,
    1.5,
    2.0,
    0.0,
    -0.5,
    -1.0,
    -1.5,
    -2.0,
]

plt.figure(figsize=(6, 6))

for x0 in initial_conditions:
    x_t = x0 * np.exp(-t)
    (line,) = plt.plot(t, x_t)
    color = line.get_color()
    for i in range(0, len(t) - 1, 50):
        plt.arrow(
            t[i],
            x_t[i],
            t[i + 1] - t[i],
            x_t[i + 1] - x_t[i],
            shape="full",
            lw=0,
            length_includes_head=True,
            head_width=0.1,
            color=color,
        )


plt.title(r"$x(t) = e^{-t} x_0$", fontsize=19)
plt.xlabel("t", fontsize=16)
plt.ylabel("x", fontsize=16)
plt.grid(True)

plt.xlim(-2, 2)
plt.ylim(-2, 2)

plt.show()



2次元線形ベクトル場

2次元線形ベクトル場は

A = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}

として次の式で定義される。

\dot{\vec{x}} = A \vec{x}, \quad \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} \in \mathbb{R}^2

2次正方行列 A の固有方程式は2次方程式なので、以下の3パターンに分かれる。

  1. 固有方程式は相異なる2つの実根をもつ
  2. 固有方程式は1つの重根をもつ
  3. 固有方程式は複素共役な2つの虚根をもつ

相異なる2つの実根をもつ場合

固有方程式の相異なる2つの実根を a, b（a < b）とする。a,b に対する固有ベクトルをそれぞれ \vec{p}, \vec{q} とすると、a \ne b より A は P=(\vec{p},\vec{q}) で対角化できる。

P^{-1} A P = \begin{pmatrix} a & 0 \\ 0 & b \end{pmatrix}

\vec{x} に対して、次のような座標変換を考える。

\vec{x} = P \vec{u}, \quad \vec{u} = \begin{pmatrix} u \\ v \end{pmatrix} \in \mathbb{R}^2

\vec{u}-平面上でのベクトル場の様子を調べる。

\begin{align*} &\dot{\vec{u}} = P^{-1} \dot{\vec{x}} = P^{-1} A \vec{x} = P^{-1} A P \vec{u} = \begin{pmatrix} a & 0 \\ 0 & b \end{pmatrix} \vec{u} \\ &\begin{cases} \dot{u} = au \\ \dot{v} = bv \end{cases} \end{align*}

t=0 のとき、(u,v) = (u_0, v_0) を通る軌道は

\begin{cases} u(t) = e^{at} u_0 \\ v(t) = e^{bt} v_0 \end{cases}

で表される。それぞれ1次元線形ベクトル場と同じなので、この場合の \vec{u}-平面における2次元線形ベクトル場の挙動はそれぞれの合成である。また、x-平面上の流れは \vec{x} = P \vec{u} と変換すればよい。

固有値 (a,b) = (-1, -0.5), (-1, 0.5) の場合の流れは次の通りである。矢印は時間の向きを指す。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(0, 10, 400)

a = -1.0
b = -0.5

initial_conditions = [
    (0.5, 1.0),
    (1.0, 0.5),
    (1.5, 2.0),
    (-0.5, -1.0),
    (-1.0, -0.5),
    (-1.5, -2.0),
    (0.5, -1.0),
    (1.0, -0.5),
    (1.5, -2.0),
    (-0.5, 1.0),
    (-1.0, 0.5),
    (-1.5, 2.0),
    (0.0, 1.0),
    (0.0, -1.0),
    (1.0, 0.0),
    (-1.0, 0.0),
]
plt.figure(figsize=(6, 6))

for u0, v0 in initial_conditions:
    u_t = u0 * np.exp(a * t)
    v_t = v0 * np.exp(b * t)
    plt.plot(u_t, v_t, color="black")
    i = 20
    plt.arrow(
        u_t[i],
        v_t[i],
        u_t[i + 1] - u_t[i],
        v_t[i + 1] - v_t[i],
        shape="full",
        lw=0,
        length_includes_head=True,
        head_width=0.06,
        color="black",
    )

plt.title(r"$u(t) = e^{-t} u_0$ and $v(t) = e^{-0.5t} v_0$", fontsize=19)
plt.xlabel("u", fontsize=16)
plt.ylabel("v", fontsize=16)
plt.grid(True)

plt.xlim(-1, 1)
plt.ylim(-1, 1)

plt.show()

import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(0, 10, 400)

a = -1.0
b = 0.5

initial_conditions = [
    (-1.0, 0.5),
    (1.0, 0.5),
    (-1.0, -0.5),
    (1.0, -0.5),
    (-1.0, 0.25),
    (1.0, 0.25),
    (-1.0, -0.25),
    (1.0, -0.25),
    (-1.0, 0.1),
    (1.0, 0.1),
    (-1.0, -0.1),
    (1.0, -0.1),
    (0.0, 0.01),
    (0.0, -0.01),
    (1.0, 0.0),
    (-1.0, 0.0),
]
plt.figure(figsize=(6, 6))

for u0, v0 in initial_conditions:
    u_t = u0 * np.exp(a * t)
    v_t = v0 * np.exp(b * t)
    plt.plot(u_t, v_t, color="black")
    if (u0, v0) == (1.0, 0.0) or (u0, v0) == (-1.0, 0.0):
        i = 40
    elif (u0, v0) == (0.0, 0.01) or (u0, v0) == (0.0, -0.01):
        i = 300
    else:
        i = 50
    plt.arrow(
        u_t[i],
        v_t[i],
        u_t[i + 1] - u_t[i],
        v_t[i + 1] - v_t[i],
        shape="full",
        lw=0,
        length_includes_head=True,
        head_width=0.06,
        color="black",
    )

plt.title(r"$u(t) = e^{-t} u_0$ and $v(t) = e^{0.5t} v_0$", fontsize=19)
plt.xlabel("u", fontsize=16)
plt.ylabel("v", fontsize=16)
plt.grid(True)

plt.xlim(-1, 1)
plt.ylim(-1, 1)

plt.show()


1つの重根をもつ場合

固有方程式の重根を a とする。このとき、\text{rank}(aI - A) は 0 か 1 である。

rankが0のとき
A = aI = \begin{pmatrix} a & 0 \\ 0 & a \end{pmatrix}

t=0 のとき、(u,v) = (u_0, v_0) を通る軌道は

\begin{cases} u(t) = e^{at} u_0 \\ v(t) = e^{at} v_0 \end{cases}

で表される。固有値 a = -1 の場合の流れは次のようになる（a = 1 は矢印の向きが変わるだけ）。

Pythonプログラム
import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(0, 10, 400)

a = -1.0

initial_conditions = [
    (0.5, 1.0),
    (1.0, 0.5),
    (1.5, 2.0),
    (-0.5, -1.0),
    (-1.0, -0.5),
    (-1.5, -2.0),
    (0.5, -1.0),
    (1.0, -0.5),
    (1.5, -2.0),
    (-0.5, 1.0),
    (-1.0, 0.5),
    (-1.5, 2.0),
    (0.0, 1.0),
    (0.0, -1.0),
    (1.0, 0.0),
    (-1.0, 0.0),
]
plt.figure(figsize=(6, 6))

for u0, v0 in initial_conditions:
    u_t = u0 * np.exp(a * t)
    v_t = v0 * np.exp(a * t)
    plt.plot(u_t, v_t, color="black")
    i = 20
    plt.arrow(
        u_t[i],
        v_t[i],
        u_t[i + 1] - u_t[i],
        v_t[i + 1] - v_t[i],
        shape="full",
        lw=0,
        length_includes_head=True,
        head_width=0.06,
        color="black",
    )

plt.title(r"$u(t) = e^{-t} u_0$ and $v(t) = e^{-t} v_0$", fontsize=19)
plt.xlabel("u", fontsize=16)
plt.ylabel("v", fontsize=16)
plt.grid(True)

plt.xlim(-1, 1)
plt.ylim(-1, 1)

plt.show()

rankが1のとき

A のジョルダン標準形を求める。固有値 a に対する固有ベクトルを \vec{p} \in \mathbb{R}^2 とする。また、(A - aI)\vec{q} = \vec{p} となる \vec{q} \in \mathbb{R}^2 を求めると、\vec{p}, \vec{q} は1次独立である。P = (\vec{p}, \vec{q}) とおくと、

\begin{align*} &\begin{cases} A \vec{p} = a \vec{p} \\ A \vec{q} = \vec{p} + a \vec{q} \end{cases}\\ &A(\vec{p}, \vec{q}) = (\vec{p}, \vec{q}) \begin{pmatrix} a & 1 \\ 0 & a \end{pmatrix} \\ & P^{-1} A P = \begin{pmatrix} a & 1 \\ 0 & a \end{pmatrix} \end{align*}

\vec{x} に対して、次のような座標変換を考える。

\vec{x} = P \vec{u}, \quad \vec{u} = \begin{pmatrix} u \\ v \end{pmatrix} \in \mathbb{R}^2

\vec{u}-平面上でのベクトル場の様子を調べる。

\begin{align*} &\dot{\vec{u}} = P^{-1} \dot{\vec{x}} = P^{-1} A \vec{x} = P^{-1} A P \vec{u} = \begin{pmatrix} a & 1 \\ 0 & a \end{pmatrix} \vec{u} \\ &\begin{cases} \dot{u} = au + v\\ \dot{v} = av \end{cases} \end{align*}

t=0 のとき、(u,v) = (u_0, v_0) を通る軌道は

\begin{cases} u(t) = e^{at} (u_0 + t v_0) \\ v(t) = e^{at} v_0 \end{cases}

で表される。固有値 a = -1 の場合の流れは次のようになる（a = 1 は矢印の向きが変わるだけ）。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(0, 10, 400)

a = -1.0

initial_conditions = [
    (0.5, 1.0),
    (1.0, 0.5),
    (1.5, 2.0),
    (-0.5, -1.0),
    (-1.0, -0.5),
    (-1.5, -2.0),
    (0.5, -1.0),
    (1.0, -0.5),
    (1.5, -2.0),
    (-0.5, 1.0),
    (-1.0, 0.5),
    (-1.5, 2.0),
    (0.0, 1.0),
    (0.0, -1.0),
    (1.0, 0.0),
    (-1.0, 0.0),
]
plt.figure(figsize=(6, 6))

for u0, v0 in initial_conditions:
    u_t = (np.array([u0 for _ in range(len(t))]) + t * v0) * np.exp(a * t)
    v_t = v0 * np.exp(a * t)
    plt.plot(u_t, v_t, color="black")
    i = 20
    plt.arrow(
        u_t[i],
        v_t[i],
        u_t[i + 1] - u_t[i],
        v_t[i + 1] - v_t[i],
        shape="full",
        lw=0,
        length_includes_head=True,
        head_width=0.06,
        color="black",
    )

plt.title(r"$u(t) = e^{-t} (u_0 + t v_0)$ and $v(t) = e^{-t} v_0$", fontsize=19)
plt.xlabel("u", fontsize=16)
plt.ylabel("v", fontsize=16)
plt.grid(True)

plt.xlim(-1, 1)
plt.ylim(-1, 1)

plt.show()

複素共役な2つの虚根をもつ場合

固有方程式の複素共役な2つの虚根を a + ib, a - ib, b>0 とする。a + ib に対する固有ベクトルを \vec{z} \in \mathbb{C}^2 として、その実部・虚部をそれぞれ \vec{p}, \vec{q} \in \mathbb{R}^2 とする。

\vec{z} = \vec{p} + i \vec{q}

このとき、\vec{p} と \vec{q} は1次独立となる。P = (\vec{p}, \vec{q}) とおくと

\begin{align*} &A\vec{z} = (a + ib) \vec{z} \\ &A\vec{p} + i A\vec{q} \\ &\begin{cases} A\vec{p} = a \vec{p} - b \vec{q} \\ A\vec{q} = b \vec{p} + a \vec{q} \end{cases}\\ &A(\vec{p}, \vec{q}) = (\vec{p}, \vec{q}) \begin{pmatrix} a & b \\ -b & a \end{pmatrix} \\ &P^{-1} A P = \begin{pmatrix} a & b \\ -b & a \end{pmatrix} \end{align*}

\vec{x} に対して、次のような座標変換を考える。

\vec{x} = P \vec{u}, \quad \vec{u} = \begin{pmatrix} u \\ v \end{pmatrix} \in \mathbb{R}^2

\vec{u}-平面上でのベクトル場の様子を調べる。

\begin{align*} &\dot{\vec{u}} = P^{-1} \dot{\vec{x}} = P^{-1} A \vec{x} = P^{-1} A P \vec{u} = \begin{pmatrix} a & b \\ -b & a \end{pmatrix} \vec{u} \\ &\begin{cases} \dot{u} = au + bv\\ \dot{v} = -bu + av \end{cases} \end{align*}

t=0 のとき、(u,v) = (u_0, v_0) を通る軌道は

\begin{cases} u(t) = e^{at} (u_0 \cos bt + v_0 \sin bt) \\ v(t) = e^{at} (v_0 \cos bt - u_0 \sin bt) \end{cases}

で表される。固有値 -0.1 \pm i, \pm i の場合の流れは次のようになる。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

t = np.linspace(0, 100, 4000)

a = -0.1
b = 1

initial_conditions = [
    (-1.0, 1.0),
]
plt.figure(figsize=(6, 6))

for u0, v0 in initial_conditions:
    u_t = (u0 * np.sin(b * t) + v0 * np.cos(b * t)) * np.exp(a * t)
    v_t = (u0 * np.cos(b * t) - v0 * np.sin(b * t)) * np.exp(a * t)
    plt.plot(u_t, v_t, color="black")
    ii = [150, 200, 300, 400, 500]
    for i in ii:
        plt.arrow(
            u_t[i],
            v_t[i],
            u_t[i + 1] - u_t[i],
            v_t[i + 1] - v_t[i],
            shape="full",
            lw=0,
            length_includes_head=True,
            head_width=0.06,
            color="black",
        )

plt.title(r"固有値$-0.1 \pm i$", fontsize=19)
plt.xlabel("u", fontsize=16)
plt.ylabel("v", fontsize=16)
plt.grid(True)

plt.xlim(-1, 1)
plt.ylim(-1, 1)

plt.show()

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

t = np.linspace(0, 10, 400)

a = 0.0
b = 1

initial_conditions = [
    (0.1, 0.1),
    (0.2, 0.2),
    (0.4, 0.4),
    (0.6, 0.6),
    (0.8, 0.8),
]
plt.figure(figsize=(6, 6))

for u0, v0 in initial_conditions:
    u_t = (u0 * np.sin(b * t) + v0 * np.cos(b * t)) * np.exp(a * t)
    v_t = (u0 * np.cos(b * t) - v0 * np.sin(b * t)) * np.exp(a * t)
    plt.plot(u_t, v_t, color="black")
    i = 50
    plt.arrow(
        u_t[i],
        v_t[i],
        u_t[i + 1] - u_t[i],
        v_t[i + 1] - v_t[i],
        shape="full",
        lw=0,
        length_includes_head=True,
        head_width=0.06,
        color="black",
    )

plt.title(r"固有値$\pm i$", fontsize=19)
plt.xlabel("u", fontsize=16)
plt.ylabel("v", fontsize=16)
plt.grid(True)

plt.xlim(-1, 1)
plt.ylim(-1, 1)

plt.show()


3次元線形ベクトル場も同様に固有方程式の根を分類し、それぞれ標準化して連立微分方程式を解くと求まる。詳細は参考文献を参照のこと。

3. 離散時間力学系

連続時間力学系が微分方程式であったのに対して、離散時間力学系は差分方程式で記述される。点 \vec{x} \in \mathbb{R}^n および連続写像 f: \mathbb{R}^n \rightarrow \mathbb{R}^n について、差分方程式は

\vec{x}(t + 1) = f(\vec{x}(t)) \quad (t = 0, 1, 2, \cdots)

で与えられる。これを単に写像という。

点 \vec{x_0} \in \mathbb{R}^n に対して、

\vec{x}_{t+1} = f(\vec{x}_t) \quad (t = 0, 1, 2, \cdots)

で与えられる点列 \{ \vec{x}_t : t = 0, 1, 2, \cdots \} を点 \vec{x_0} を通る正の半軌道という。

f が同相写像であれば可逆系、そうでなければ非可逆系という。可逆系の場合は負の時間方向への軌道を考えることができる。点 \vec{x_0} \in \mathbb{R}^n に対して、

\vec{x}_{t-1} = f(\vec{x}_t) \quad (t = 0, -1, -2, \cdots)

で与えられる点列 \{ \vec{x}_t : t = 0, -1, -2, \cdots \} を正の半軌道に加えて得られる点列 \{ \vec{x}_t : t = 0, \pm 1, \pm 2, \cdots \} を \vec{x_0} を通る軌道という。

線形写像

線形ベクトル場と同様に線形写像を考える。その解析方法は線形ベクトル場と同じなので、ダイジェスト形式で紹介する。

A を n 次元正方行列とする。

\vec{x} \mapsto A \vec{x}, \quad \vec{x} \in \mathbb{R}^n

で定義される \mathbb{R}^n 上の離散時間力学系を線形写像という。

1次元線形写像

a を実定数として

x \mapsto ax, \quad x \in \mathbb{R}

で定義される。t = 0 のとき x = x_0 を通る軌道は

x(t) = a^t x_0, \quad t = 0, \pm 1, \pm 2, \cdots

で表される。a の符号によって挙動が次のように変わる。

pythonプログラム
import matplotlib.pyplot as plt
import numpy as np

t = np.arange(0, 20, 1)

a_values = [1.25, 0.8, -0.8, -1.25]
initial_values = [1, -1]

fig, axs = plt.subplots(2, 2, figsize=(12, 10))

for i, a in enumerate(a_values):
    ax = axs[i // 2, i % 2]

    if a in [1.25, 0.8]:
        for x_0 in initial_values:
            x_t = x_0 * (a**t)
            ax.plot(t, x_t, marker="o", label=f"x_0 = {x_0}, a = {a}")
            for j in range(len(t) - 1):
                ax.annotate(
                    "",
                    xy=(t[j + 1], x_t[j + 1]),
                    xytext=(t[j], x_t[j]),
                    arrowprops=dict(arrowstyle="->", color="black"),
                )
    else:
        x_0 = 1
        x_t = x_0 * (a**t)
        ax.plot(t, x_t, marker="o", label=f"x_0 = {x_0}, a = {a}")
        for j in range(len(t) - 1):
            ax.annotate(
                "",
                xy=(t[j + 1], x_t[j + 1]),
                xytext=(t[j], x_t[j]),
                arrowprops=dict(arrowstyle="->", color="black"),
            )

    ax.set_title(f"a = {a}", fontsize=19)
    ax.set_xlabel("t", fontsize=16)
    ax.set_ylabel("x(t)", fontsize=16)
    ax.grid(True)

plt.tight_layout()
plt.show()

2次元線形写像

2次元線形写像は

A = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}

として次の式で定義される。

\vec{x} \mapsto A \vec{x}, \quad \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} \in \mathbb{R}^2

2次正方行列 A の固有方程式は2次方程式なので、以下の3パターンに分かれる。

  1. 固有方程式は相異なる2つの実根をもつ
  2. 固有方程式は1つの重根をもつ
  3. 固有方程式は複素共役な2つの虚根をもつ
相異なる2つの実根をもつ場合

固有値を a, b とすると、t = 0 のとき (x,y) = (x_0, y_0) を通る軌道は

\begin{cases} x(t) = a^t x_0\\ y(t) = b^t y_0, \quad t = 0, \pm 1, \pm 2, \cdots \end{cases}

で表される。各固有値のパターンでのシミュレーション結果は次のようになる。

pythonプログラム
import matplotlib.pyplot as plt
import numpy as np

t = np.arange(0, 25, 1)

# a, bの値のリストとそれぞれの初期値のリスト
eigenvalues_and_initial_values = [
    (
        (0.8, 0.9),
        [
            (1, 1),
            (-1, 1),
            (1, -1),
            (-1, -1),
            (1, 0.5),
            (1, 0),
            (1, -0.5),
            (-1, 0.5),
            (-1, 0),
            (-1, -0.5),
        ],
    ),
    (
        (0.8, 1.25),
        [
            (-1, 0),
            (1, 0),
            (0, 0.01),
            (0, -0.01),
            (-1, 0.1),
            (-1, -0.1),
            (1, 0.1),
            (1, -0.1),
        ],
    ),
    ((-0.8, 1.25), [(1, 0.1), (-1, -0.1)]),
    ((-0.8, -1.25), [(0.5, -0.5), (-0.5, 0.5), (-0.3, -0.3), (0.3, 0.3)]),
]

fig, axs = plt.subplots(2, 2, figsize=(12, 10))

for i, ((a, b), initial_values) in enumerate(eigenvalues_and_initial_values):
    ax = axs[i // 2, i % 2]

    for x_0, y_0 in initial_values:
        x_t = x_0 * (a**t)
        y_t = y_0 * (b**t)

        ax.scatter(x_t, y_t, marker="o")
        for j in range(len(t) - 1):
            ax.annotate(
                "",
                xy=(x_t[j + 1], y_t[j + 1]),
                xytext=(x_t[j], y_t[j]),
                arrowprops=dict(arrowstyle="->", color="black"),
            )

    ax.set_title(f"a = {a}, b = {b}", fontsize=19)
    ax.set_xlabel("x(t)", fontsize=16)
    ax.set_ylabel("y(t)", fontsize=16)
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.grid(True)

plt.tight_layout()
plt.show()

1つの重根をもつ場合

重根を a \in \mathbb{R} とする。

階数が0のとき、t = 0 のとき (x,y) = (x_0, y_0) を通る軌道は

\begin{cases} x(t) = a^t x_0 \\ y(t) = a^t y_0, \quad t = 0, \pm 1, \pm 2, \cdots \end{cases}

で表される。相空間での軌道は次のようになる。

pythonプログラム
import matplotlib.pyplot as plt
import numpy as np

t = np.arange(0, 25, 1)

# aの値とそれぞれの初期値のリスト
a_values_and_initial_values = [
    (
        -0.8,
        [
            (0.5, 1.0),
            (1.0, 0.5),
            (1.5, 2.0),
            (-0.5, -1.0),
            (-1.0, -0.5),
            (-1.5, -2.0),
            (0.5, -1.0),
            (1.0, -0.5),
            (1.5, -2.0),
            (-0.5, 1.0),
            (-1.0, 0.5),
            (-1.5, 2.0),
            (0.0, 1.0),
            (0.0, -1.0),
            (1.0, 0.0),
            (-1.0, 0.0),
        ],
    ),
    (
        0.8,
        [
            (0.5, 1.0),
            (1.0, 0.5),
            (1.5, 2.0),
            (-0.5, -1.0),
            (-1.0, -0.5),
            (-1.5, -2.0),
            (0.5, -1.0),
            (1.0, -0.5),
            (1.5, -2.0),
            (-0.5, 1.0),
            (-1.0, 0.5),
            (-1.5, 2.0),
            (0.0, 1.0),
            (0.0, -1.0),
            (1.0, 0.0),
            (-1.0, 0.0),
        ],
    ),
]

fig, axs = plt.subplots(1, 2, figsize=(12, 6))

for i, (a, initial_values) in enumerate(a_values_and_initial_values):
    ax = axs[i]

    for x_0, y_0 in initial_values:
        x_t = x_0 * (a**t)
        y_t = y_0 * (a**t)

        ax.scatter(x_t, y_t, marker="o")
        for j in range(len(t) - 1):
            if abs(x_t[j + 1]) <= 1 and abs(y_t[j + 1]) <= 1:
                ax.annotate(
                    "",
                    xy=(x_t[j + 1], y_t[j + 1]),
                    xytext=(x_t[j], y_t[j]),
                    arrowprops=dict(arrowstyle="->", color="black"),
                )

    ax.set_title(f"a = {a}", fontsize=19)
    ax.set_xlabel("x(t)", fontsize=16)
    ax.set_ylabel("y(t)", fontsize=16)
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.grid(True)

plt.tight_layout()
plt.show()

階数が1のとき、t = 0 のとき (x,y) = (x_0, y_0) を通る軌道は

\begin{cases} x(t) = a^t x_0 + t a^{t-1} y_0 \\ y(t) = a^t y_0, \quad t = 0, \pm 1, \pm 2, \cdots \end{cases}

で表される。相空間での軌道は次のようになる。

pythonプログラム
import matplotlib.pyplot as plt
import numpy as np

t = np.arange(0, 30, 1)

eigenvalues_and_initial_values = [
    (
        -1,
        [
            (1, 1),
            (-1, 1),
            (1, -1),
            (-1, -1),
            (1, 0.5),
            (1, 0),
            (1, -0.5),
            (-1, 0.5),
            (-1, 0),
            (-1, -0.5),
        ],
    ),
    (
        0.6,
        [
            (-1, 0),
            (1, 0),
            (-1, 1),
            (1, -1),
            (-1, 0.5),
            (1, -0.5),
        ],
    ),
    (
        1,
        [
            (-1, 0.8),
            (-1, 0.6),
            (-1, 0.3),
            (1, -0.8),
            (1, -0.6),
            (1, -0.3),
        ],
    ),
    (
        1.5,
        [
            (-0.01, 0),
            (0.01, 0),
            (-0.05, 0.01),
            (0.05, -0.01),
            (-0.15, 0.03),
            (0.15, -0.03),
        ],
    ),
]

fig, axs = plt.subplots(2, 2, figsize=(12, 10))

for i, (a, initial_values) in enumerate(eigenvalues_and_initial_values):
    ax = axs[i // 2, i % 2]

    for x_0, y_0 in initial_values:
        x_t = x_0 * (a ** t[1:]) + y_0 * t[1:] * (a ** (t[1:] - 1))
        x_t = np.insert(x_t, 0, x_0)
        y_t = y_0 * (a**t)
        if i == 0:
            ax.scatter(x_t, y_t, marker="o")
        else:
            ax.plot(x_t, y_t, marker="o")
        for j in range(len(t) - 1):
            ax.annotate(
                "",
                xy=(x_t[j + 1], y_t[j + 1]),
                xytext=(x_t[j], y_t[j]),
                arrowprops=dict(arrowstyle="->", color="black"),
            )

    ax.set_title(f"a = {a}", fontsize=19)
    ax.set_xlabel("x(t)", fontsize=16)
    ax.set_ylabel("y(t)", fontsize=16)
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.grid(True)

plt.tight_layout()
plt.show()

複素共役な2つの虚根をもつ場合

2つの複素共役な固有値を a \pm ib（a, b \in \mathbb{R}）とする。実数 r, \theta を

r = \sqrt{a^2 + b^2}, \quad \cos \theta = \frac{a}{r}, \quad \sin \theta = \frac{b}{r}

によって定義すると、t=0 のとき (x,y) = (x_0, y_0) を通る軌道は

\begin{cases} x(t) = r^t (x_0 \cos \theta t + y_0 \sin \theta t) \\ y(t) = r^t (-x_0 \sin \theta t + y_0 \cos \theta t), \quad t = 0, \pm 1, \pm 2, \cdots \end{cases}

で表される。r の絶対値によって軌道の様子が変化する。負の場合は振動したり発散したりする。

pythonプログラム
import matplotlib.pyplot as plt
import numpy as np

t = np.arange(0, 60, 1)

# r, θの値のリストとそれぞれの初期値のリスト
r_theta_and_initial_values = [
    ((0.95, np.pi / 10), [(1, 1), (-1, 1)]),
    ((1, np.pi / 10), [(0, 0.25), (0, 0.5), (0, 0.75)]),
    ((1.1, np.pi / 10), [(0.01, 0.01), (-0.01, 0.01)]),
]

fig, axs = plt.subplots(1, 3, figsize=(18, 6))

for i, ((r, theta), initial_values) in enumerate(r_theta_and_initial_values):
    ax = axs[i]

    for x_0, y_0 in initial_values:
        x_t = r**t * (x_0 * np.cos(theta * t) + y_0 * np.sin(theta * t))
        y_t = r**t * (-x_0 * np.sin(theta * t) + y_0 * np.cos(theta * t))

        ax.plot(x_t, y_t, marker="o", label=f"x_0 = {x_0}, y_0 = {y_0}")
        for j in range(len(t) - 1):
            if abs(x_t[j + 1]) <= 1 and abs(y_t[j + 1]) <= 1:
                ax.annotate(
                    "",
                    xy=(x_t[j + 1], y_t[j + 1]),
                    xytext=(x_t[j], y_t[j]),
                    arrowprops=dict(arrowstyle="->", color="black"),
                )

    ax.set_title(f"r = {r}, " + r"$\theta = \pi / 10$", fontsize=19)
    ax.set_xlabel("x(t)", fontsize=16)
    ax.set_ylabel("y(t)", fontsize=16)
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.grid(True)

plt.tight_layout()
plt.show()

4. ベクトル場の平衡点の分岐

単振り子の節で見たように、パラメータを変化させたときに力学系の振る舞いが質的に変化する現象を分岐現象という。パラメータ \mu \in \mathbb{R}^p をもつ自律系のベクトル場

\dot{\vec{x}} = f(\vec{x},\mu), \quad \vec{x} \in \mathbb{R}^n

を考える。パラメータ \mu = \mu_0 のとき \dot{\vec{x}} が \vec{0} になる点、すなわち

f(\vec{x}_0, \mu_0) = \vec{0}

を満たす点 \vec{x} = \vec{x}_0 を平衡点という。つまり、平衡点はすべての時刻において静止している状態を表す。原点 O は任意の線形ベクトル場の平衡点である。

平衡点から少しずれたときにどのような挙動をするかを調べることを安定性解析という。安定性にはいくつか定義があるが、今回は漸近安定性を紹介する。漸近安定性は、平衡点の近くにある点が時間とともに平衡点に収束することを意味する。

漸近安定性を判定するためには平衡点からの微小のずれ（変分）に注目すればよい。点 \vec{x}_0 \in \mathbb{R}^n を平衡点とし、そこからの変分を \xi(t) とする。変分に対する方程式を得るため

\vec{x}(t) = \vec{x}_0 + \xi(t)

の運動を考える。

\dot{\vec{x}}(t) = \dot{\vec{x}}_0 + \dot{\xi}(t) = f(\vec{x}_0 + \xi(t))

変分 \xi(t) を十分小さいとすると、平衡点 \vec{x}_0 周りでテイラー展開して、

f(\vec{x}_0 + \xi(t)) = f(\vec{x}_0) + \left. \frac{\partial f}{\partial \vec{x}} \right|_{\vec{x}(t) = \vec{x}_0} \xi(t) + O(\xi^2(t))

1次近似すると、

\dot{\xi}(t) = A \xi(t)

という線形ベクトル場を得る。ここで、

A = D_{\vec{x}} f(\vec{x}_0) = \left. \frac{\partial f}{\partial \vec{x}} \right|_{\vec{x}(t) = \vec{x}_0} = \left( \left. \frac{\partial f_i}{\partial x_j} \right|_{\vec{x}(t) = \vec{x}_0} \right)_{1 \leq i,j \leq n}

とおいた。この A はヤコビ行列である。

A のすべての固有値の実部が非零であるとき、平衡点 \vec{x}_0 は双曲型であるという。証明は省略するが、\vec{x}_0 が双曲型で A のすべての固有値の実部が負であるとき、\vec{x}_0 は漸近安定である。また、\vec{x}_0 が双曲型で A の少なくとも1つの固有値の実部が正であるとき、\vec{x}_0 は不安定である。

前の線形ベクトル場の説明で挙げた例では、固有値の実部がすべて負であるときは原点 O に収束していたことが確認できる。つまり、この場合の1次近似が妥当な範囲の変分 \xi(t) は t \rightarrow \infty で 原点 O に収束し、平衡点 \vec{x}_0 が漸近安定であることを意味する。

（例）実際に単振り子のベクトル場で安定性を調べてみよう。まずは、摩擦や空気抵抗を無視した場合を考える（g/l=1）。

\begin{cases} \dot{\theta} = \omega \\ \dot{\omega} = -\sin \theta, \quad 0 \leq \theta < 2\pi \end{cases}

(\dot{\theta}, \dot{\omega}) = (0,0) となる平衡点 (\theta_0, \omega_0) は

\begin{cases} \theta_0 = 0, \pi \\ \omega_0 = 0 \end{cases}
  • (\theta_0, \omega_0) = (0, \pi) のとき

変分 \xi(t) \in \mathbb{R}^2 についての線形ベクトル場は、

\dot{\xi}(t) = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \xi(t)

となる。固有値は \pm 1 と正の値を含んでいるので、この平衡点は不安定である。これは直感に一致する。

  • (\theta_0, \omega_0) = (0, 0) のとき

変分 \xi(t) \in \mathbb{R}^2 についての線形ベクトル場は、

\dot{\xi}(t) = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \xi(t)

となる。固有値は \pm i と実部が 0 なので、固有値を用いた方法では判定できない。リヤプノフ関数といった別の手法を考える必要がある。

次に速度に比例する空気抵抗の項を追加する（g/l=c/m=1）。

\begin{cases} \dot{\theta} = \omega \\ \dot{\omega} = -\sin \theta - \omega, \quad 0 \leq \theta < 2\pi \end{cases}

平衡点はさきほどと同じである。(0, \pi) は変わらず不安定だが、(0,0) では面白い変化が生じる。

  • (\theta_0, \omega_0) = (0, 0) のとき

変分 \xi(t) \in \mathbb{R}^2 についての線形ベクトル場は、

\dot{\xi}(t) = \begin{pmatrix} 0 & 1 \\ -1 & -1 \end{pmatrix} \xi(t)

である。固有値は -1/2 \pm i \sqrt{3} と実部がすべて負なので、この平衡点は漸近安定である。さきほどは安定性を判定できなかった点が、空気抵抗を加えることで、固有値を使って判定できるようになった！

ベクトル場の平衡点の分岐を調べるためには次の定理が重要である。

\mu = \mu_0 において平衡点 \vec{x}_0 が双曲型であれば、パラメータ \mu = \mu_0 の近傍で変化させるとき、平衡点は持続して、安定性の型は変化しない。

この定理から、ベクトル場の平衡点の分岐を考えるには、\mu = \vec{0} のとき、原点に非双曲型平衡点をもつ場合を考えればよいことがわかる。\mu = \vec{0} や原点にしているのは単に簡単になるからという理由である。別に適当な点を取ってきてもよいが、平行移動すれば形は同じなので、特に一般性は失われない。

1次元ベクトル場

サドル・ノード分岐

1次元ベクトル場

\dot{x} = f(x, \mu)

が f(0,0) = 0, f_x(0,0) = 0 を満たすとき、

f_\mu (0,0) \ne 0, \quad f_{xx}(0,0) \ne 0

ならば、\mu = 0 のとき x=0 においてサドル・ノード分岐が生じる。そのベクトル場の標準形は

\dot{x} = \mu \mp x^2

で与えられる。マイナス符号の場合は次のような変化をする。

  • \mu < 0：平衡点をもたない。
  • \mu = 0：x = 0 に固有値 0 をもつ平衡点をもつ。
  • \mu > 0：2つの平衡点 P^+ = \sqrt{\mu}, P^- = -\sqrt{\mu} をもつ。P^+ の固有値は f_x(\sqrt{\mu}, \mu) = -2\sqrt{\mu} < 0 で安定、P^- の固有値は f_x(-\sqrt{\mu}, \mu) = 2\sqrt{\mu}>0 で不安定である。

グラフにすると次のようになる。

pythonプログラム
import matplotlib.pyplot as plt
import numpy as np

mus = np.array([-0.3, 0, 0.3])
x = np.arange(-1, 1, 0.01)

fig, axs = plt.subplots(1, 3, figsize=(18, 6))

for i, mu in enumerate(mus):
    ax = axs[i]
    xdot = mu - x * x
    ax.plot(x, xdot, linewidth=1.5, color="red")
    if i == 1:
        ax.scatter(0, 0, marker="o", s=150, color="black")
        ax.arrow(
            1.0,
            0,
            -0.7,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            0,
            0,
            -0.3,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
    elif i == 2:
        ax.scatter(np.sqrt(mu), 0, marker="o", s=150, color="black")
        ax.scatter(-np.sqrt(mu), 0, marker="o", s=150, color="blue")
        ax.arrow(
            -np.sqrt(mu),
            0,
            -0.3,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            -np.sqrt(mu),
            0,
            0.8,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            1,
            0,
            -0.2,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
    ax.set_title(rf"$\mu = {mu}$", fontsize=19)
    ax.set_xlabel(r"$x(t)$", fontsize=16)
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.axhline(0, color="black", linewidth=0.7)
    ax.axvline(0, color="black", linewidth=0.7)
    ax.grid(True)

plt.tight_layout()
plt.show()

\mu を正から負に変化させたとき、パラメータに変化にともなって、安定平衡点と不安定平衡点が近づいて合体し消滅する。以下のgifはWikipediaから引用してきたものである。

1次元ベクトル場で一般的に観測されるのはサドル・ノード分岐のみであることが知られている。ただし、拘束条件を付け加えると別の分岐が生じることがある。

トランスクリティカル分岐

トランスクリティカル分岐は原点に平衡点を持つという拘束条件を課したときに生じる分岐である。一般に1次元ベクトル場

\dot{x} = f(x, \mu)

が f(0,0) = 0, f_x(0,0) = 0 を満たすとき、

f_\mu (0,0) = 0, \quad f_{x\mu}(0,0) \ne 0 ,\quad f_{xx}(0,0) \ne 0

ならば、\mu = 0 のとき x=0 においてトランスクリティカル分岐が生じる。そのベクトル場の標準形は

\dot{x} = \mu x \mp x^2

で与えられる。マイナス符号の場合は次のような変化をする。

  • \mu < 0：平衡点 O は固有値 \mu < 0 を持ち安定、平衡点 P = \mu は固有値 -\mu > 0 を持ち不安定。
  • \mu = 0：平衡点 O は固有値 0。
  • \mu > 0：平衡点 O は固有値 \mu > 0 を持ち不安定、平衡点 P = \mu は固有値 -\mu < 0 を持ち安定。

図示すると次のようになる。平衡点の安定性が正負で交代していることがわかる。

pythonプログラム
import matplotlib.pyplot as plt
import numpy as np

mus = np.array([-0.7, 0, 0.7])
x = np.arange(-1, 1, 0.01)

fig, axs = plt.subplots(1, 3, figsize=(18, 6))

for i, mu in enumerate(mus):
    ax = axs[i]
    xdot = x * (mu - x)
    ax.plot(x, xdot, linewidth=1.5, color="red")
    if i == 0:
        ax.scatter(0, 0, marker="o", s=150, color="black")
        ax.scatter(mu, 0, marker="o", s=150, color="blue")
        ax.arrow(
            mu,
            0,
            -0.2,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            mu,
            0,
            0.3,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            1,
            0,
            -0.55,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
    elif i == 1:
        ax.scatter(0, 0, marker="o", s=150, color="blue")
        ax.arrow(
            1.0,
            0,
            -0.7,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            0,
            0,
            -0.3,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
    elif i == 2:
        ax.scatter(0, 0, marker="o", s=150, color="blue")
        ax.scatter(mu, 0, marker="o", s=150, color="black")
        ax.arrow(
            1,
            0,
            -0.1,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            0,
            0,
            0.3,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            0,
            0,
            -0.3,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
    ax.set_title(rf"$\mu = {mu}$", fontsize=19)
    ax.set_xlabel(r"$x(t)$", fontsize=16)
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.axhline(0, color="black", linewidth=0.7)
    ax.axvline(0, color="black", linewidth=0.7)
    ax.grid(True)

plt.tight_layout()
plt.show()

以下のアニメーションはWikipediaから引用してきたものである。

ピッチフォーク分岐

ベクトル場 \dot{x} = f(x, \mu) が x に関して奇関数

f(-x, \mu) = -f(x, \mu)

という拘束条件を課されたときにピッチフォーク分岐が生じる。一般に1次元ベクトル場 \dot{x} = f(x, \mu) が f(0,0) = 0, f_x(0,0) = 0 を満たすとき、

f_\mu(0,0) = f_{xx}(0,0) = 0, \quad f_{x\mu}(0,0) \ne 0, \quad f_{xxx}(0,0) \ne 0

ならば、\mu = 0 のとき x = 0 においてピッチフォーク分岐が生じる。そのベクトル場の標準形は

\dot{x} = \mu x \mp x^3

で与えられる。マイナス符号のときの分岐の様子は次のようになる。

  • \mu < 0：平衡点 O は固有値 \mu < 0 を持ち安定。
  • \mu = 0：平衡点 O は固有値 0 を持つ。
  • \mu > 0：平衡点 O は固有値 \mu > 0 を持ち不安定。平衡点 P^{\pm} = \pm \sqrt{\mu} は固有値 -2\mu を持ち安定。
pythonプログラム
import matplotlib.pyplot as plt
import numpy as np

mus = np.array([-0.5, 0, 0.5])
x = np.arange(-1, 1, 0.01)

fig, axs = plt.subplots(1, 3, figsize=(18, 6))

for i, mu in enumerate(mus):
    ax = axs[i]
    xdot = x * (mu - x * x)
    ax.plot(x, xdot, linewidth=1.5, color="red")
    if i == 0 or i == 1:
        ax.scatter(0, 0, marker="o", s=150, color="black")
        ax.arrow(
            1.0,
            0,
            -0.7,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            -1.0,
            0,
            0.7,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
    elif i == 2:
        ax.scatter(0, 0, marker="o", s=150, color="blue")
        ax.scatter(np.sqrt(mu), 0, marker="o", s=150, color="black")
        ax.scatter(-np.sqrt(mu), 0, marker="o", s=150, color="black")
        ax.arrow(
            -1,
            0,
            0.1,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            0,
            0,
            -0.5,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            0,
            0,
            0.5,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
        ax.arrow(
            1,
            0,
            -0.1,
            0,
            head_width=0.08,
            head_length=0.05,
            fc="black",
            ec="black",
            linewidth=0.7,
        )
    ax.set_title(rf"$\mu = {mu}$", fontsize=19)
    ax.set_xlabel(r"$x(t)$", fontsize=16)
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.axhline(0, color="black", linewidth=0.7)
    ax.axvline(0, color="black", linewidth=0.7)
    ax.grid(True)

plt.tight_layout()
plt.show()

負から正にパラメータを動かすと、安定平衡点 O が不安定化し、その両側に安定平衡点 P^{\pm} が発生する。見た目から熊手型分岐という可愛らしい名前もある。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import Image

plt.rcParams["figure.dpi"] = 200
plt.rcParams["font.family"] = "serif"
plt.rcParams["mathtext.fontset"] = "cm"


def f(x, mu):
    return x * (mu - x**2)


fig, ax = plt.subplots()
x = np.linspace(-4, 4, 400)
(line,) = ax.plot(x, f(x, -10), color="red", linewidth=1.5)

ax.grid(True)
ax.axhline(0, color="black", linewidth=0.7)
ax.axvline(0, color="black", linewidth=0.7)
ax.set_xlim(-4, 4)
ax.set_ylim(-30, 30)
ax.set_xlabel(r"$x$", fontsize=16)
ax.set_ylabel(r"$f(x, \mu)$", fontsize=16)
title = ax.set_title(r"$\mu = -10$", fontsize=19)

# 初期化
scatter_origin = ax.scatter(0, 0, marker="o", s=110, color="black")
scatter1 = ax.scatter([], [], marker="o", s=110, color="black")
scatter2 = ax.scatter([], [], marker="o", s=110, color="black")


def update(mu):
    line.set_ydata(f(x, mu))
    title.set_text(r"$\mu = {:.1f}$".format(mu))

    if mu >= 0:
        scatter_origin.set_color("blue")
    else:
        scatter_origin.set_color("black")

    if mu > 0:
        scatter1.set_offsets([[np.sqrt(mu), 0]])
        scatter2.set_offsets([[-np.sqrt(mu), 0]])
        scatter1.set_sizes([110])
        scatter2.set_sizes([110])
    else:
        scatter1.set_offsets([[0, 0]])
        scatter1.set_sizes([0])
        scatter2.set_offsets([[0, 0]])
        scatter2.set_sizes([0])

    return line, title, scatter_origin, scatter1, scatter2


ani = FuncAnimation(fig, update, frames=np.linspace(10, -5, 20), blit=True)
ani.save("./fig/function_animation.gif", writer="imagemagick")
plt.close(fig)

Image("./fig/function_animation.gif")

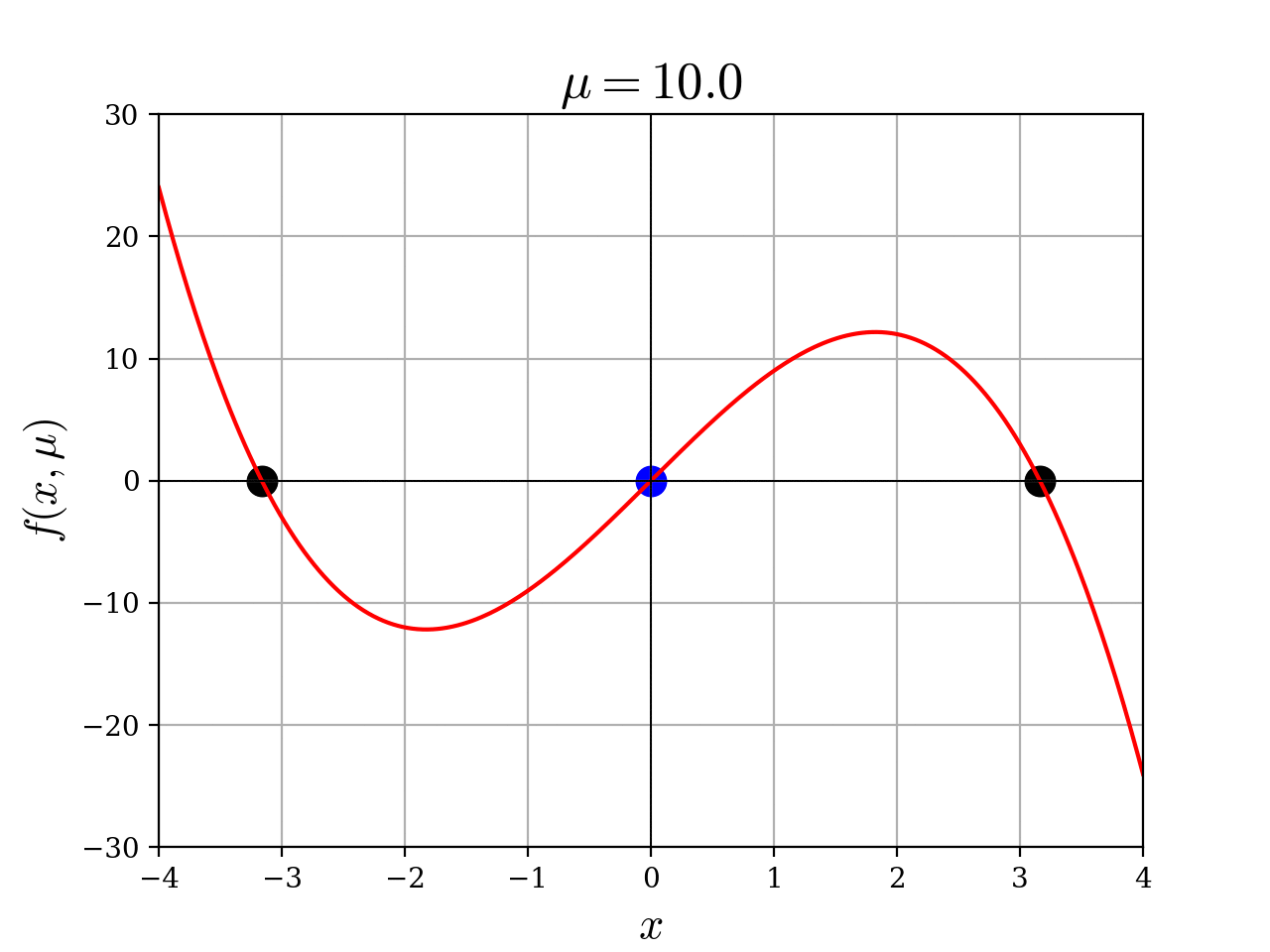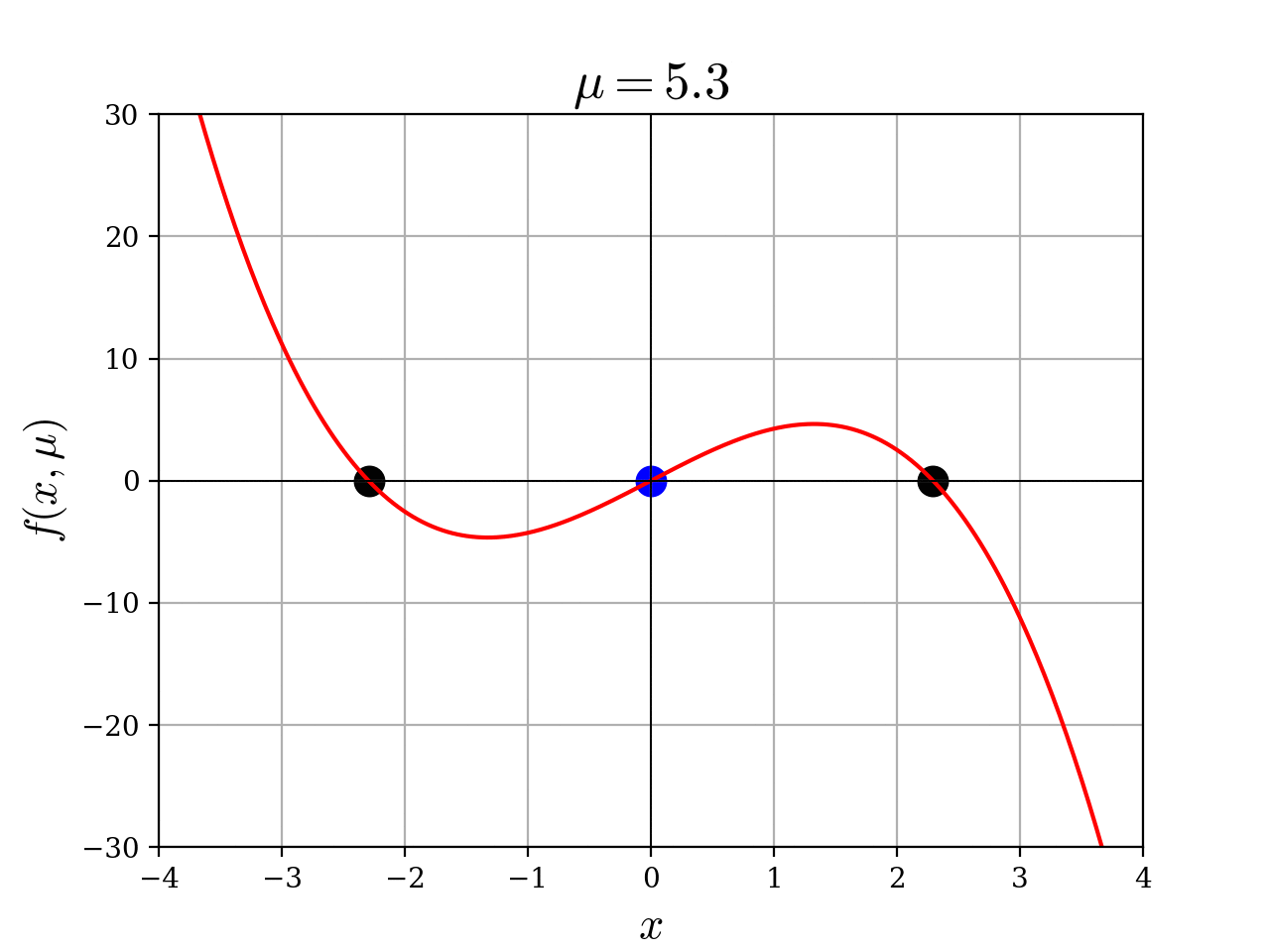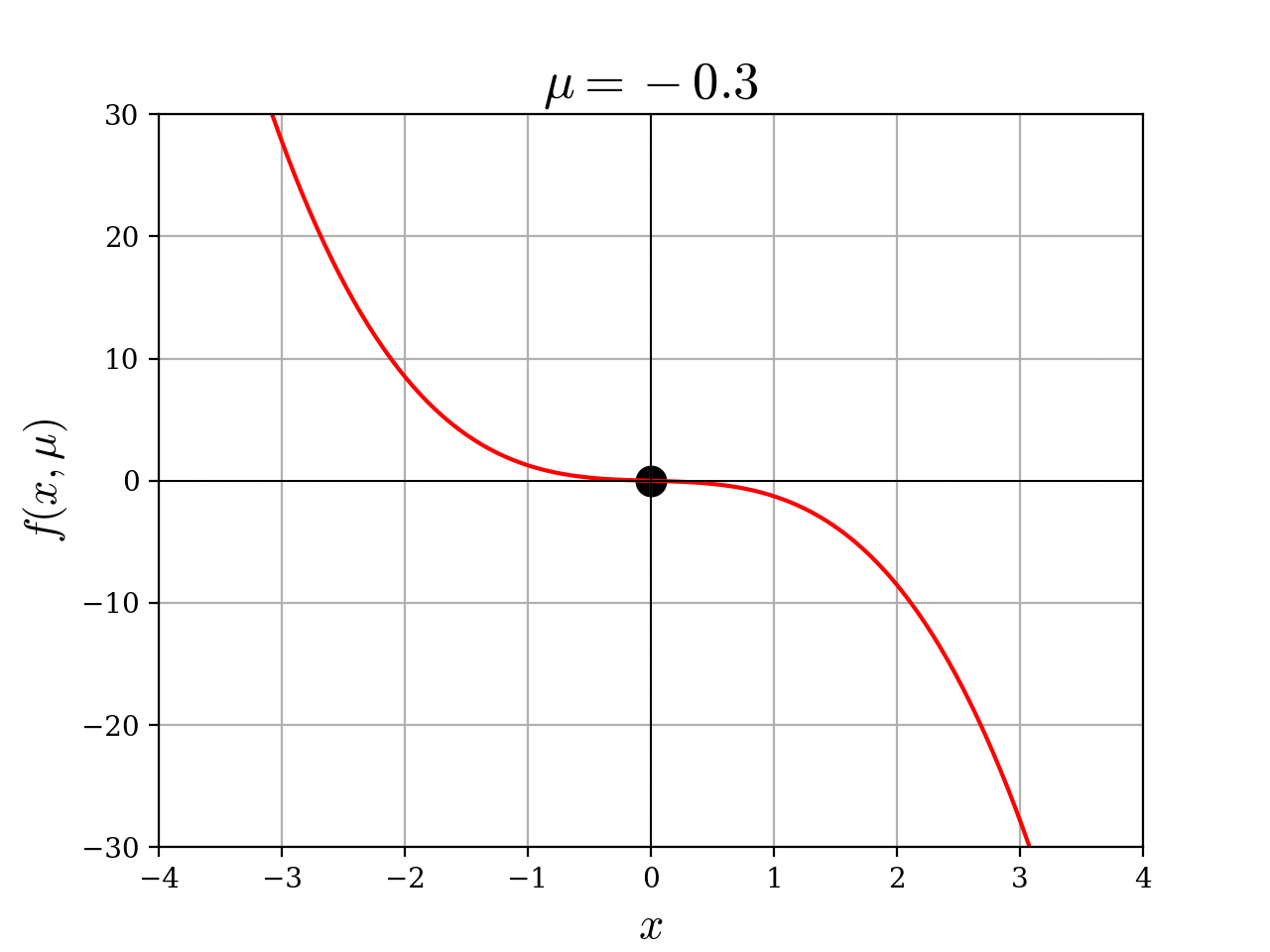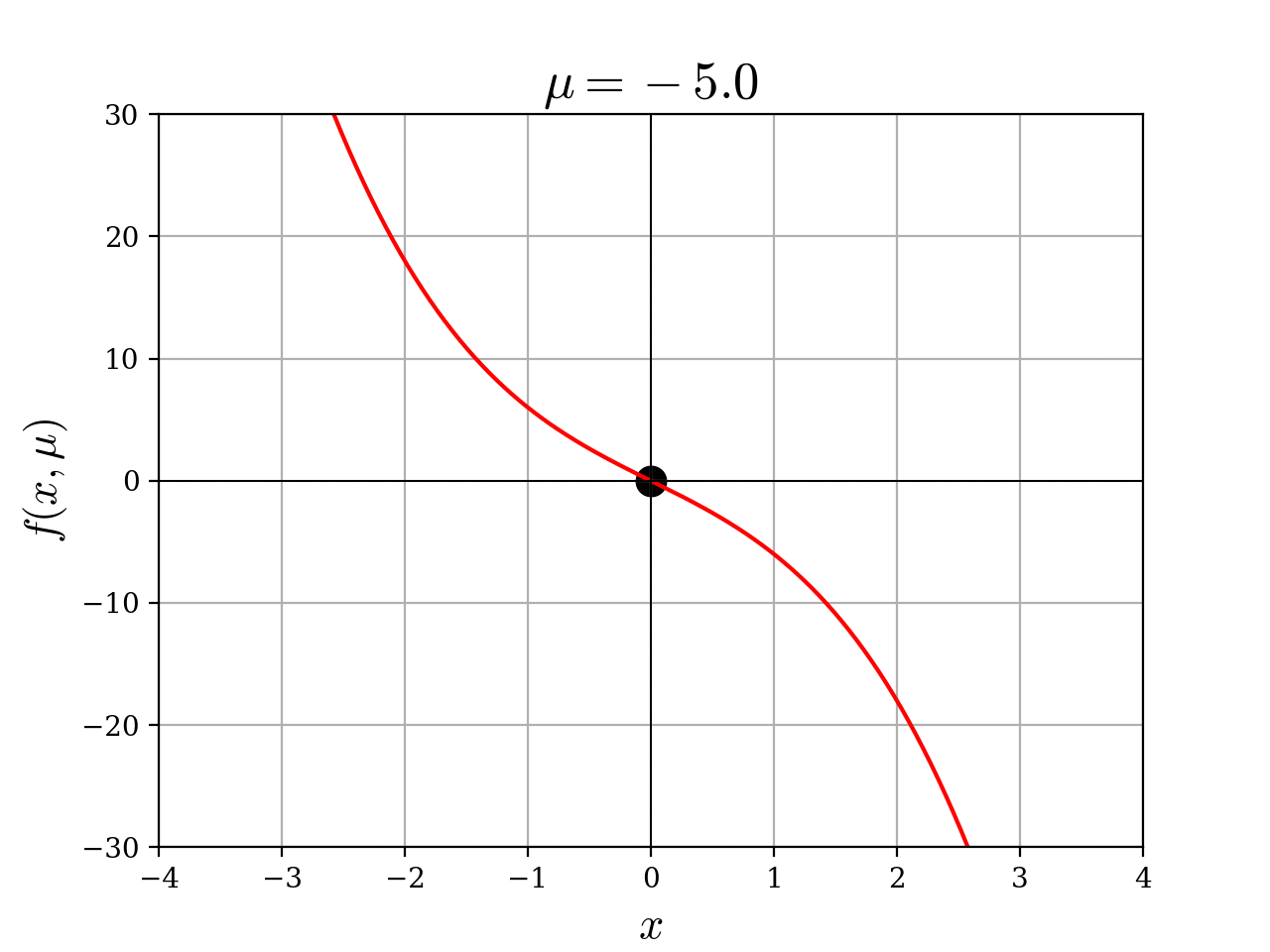
2次元ベクトル場

次に2次元ベクトル場の分岐を見ていく。

\begin{align*} &\dot{\vec{x}} = f(\vec{x}, \mu) = \left( f_1(x,y,\mu), f_2(x,y,\mu) \right)^T \\ &\vec{x} = (x, y)^T \in \mathbb{R}^2, \quad \mu \in \mathbb{R} \end{align*}

1次元と同様で、\mu = 0 のとき \vec{x} = \vec{0} に非双曲型平衡点を持つ場合を考える。ヤコビ行列

A = \begin{pmatrix} (f_1)_x & (f_1)_y \\ (f_2)_x & (f_2)_y \end{pmatrix}

が固有値の1つに0をもつ場合と、1組の複素共役固有値が純虚数になる場合の分岐を述べる。

サドル・ノード分岐

ヤコビ行列の固有値の1つに0を持つベクトル場

\begin{cases} \dot{x} = \mu - x^2 \\ \dot{y} = -y \end{cases}

を考える。分岐の様子は次のようになる。

  • \mu < 0：平衡点なし。
  • \mu = 0：平衡点 O は固有値 0, -1 を持つ。
  • \mu > 0：平衡点 P^+ = (\sqrt{\mu}, 0) は固有値 -2\sqrt{\mu}, -1 を持ち安定（ノード）。平衡点 P^- = (-\sqrt{\mu}, 0) は固有値 2\sqrt{\mu}, -1 を持ち不安定（サドル）。

図示してみると、y 軸方向の安定性は変化していないことがわかる。これはつまり1次元の分岐問題に帰着できることを示している。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp


def f(t, X, mu):
    x, y = X
    dydt = [mu - x**2, -y]
    return dydt


t_span = (0, 10)
t_eval = np.linspace(t_span[0], t_span[1], 1000)

initial_conditions_lists = [
    [
        [5, 0],
        [5, 3],
        [5, -3],
        [2, 5],
        [2, -5],
        [-1, 5],
        [-1, -5],
    ],
    [
        [5, 0],
        [-0.1, 0],
        [0, 5],
        [0, -5],
        [3, 5],
        [3, -5],
        [-1, 5],
        [-1, -5],
        [-0.5, 3],
        [-0.5, -3],
    ],
    [
        [5, 0],
        [-0.9, 0],
        [-1.1, 0],
        [0, 5],
        [0, -5],
        [1, 5],
        [1, -5],
        [3, 5],
        [3, -5],
        [-1, 5],
        [-1, -5],
        [-2, 5],
        [-2, -5],
        [-1.5, 4],
        [-1.5, -4],
    ],
]
mus = [-1, 0, 1]

fig, axs = plt.subplots(1, 3, figsize=(18, 6))

for i, mu in enumerate(mus):
    ax = axs[i]

    for initial_conditions in initial_conditions_lists[i]:
        sol = solve_ivp(f, t_span, initial_conditions, args=(mu,), t_eval=t_eval)
        ax.plot(sol.y[0], sol.y[1], color="black")

        idx = len(sol.t) // 3
        ax.annotate(
            "",
            xy=(sol.y[0][idx], sol.y[1][idx]),
            xytext=(sol.y[0][idx - 1], sol.y[1][idx - 1]),
            arrowprops=dict(arrowstyle="->", color="black", mutation_scale=20),
        )

    ax.grid(True)
    ax.set_xlim(-5, 5)
    ax.set_ylim(-5, 5)
    ax.set_xlabel(r"$x$", fontsize=16)
    ax.set_ylabel(r"$y$", fontsize=16)
    if i == 0:
        ax.set_title(r"$\mu < 0$", fontsize=19)
    elif i == 1:
        ax.scatter(0, 0, marker="o", s=150, color="black")
        ax.set_title(r"$\mu = 0$", fontsize=19)
    elif i == 2:
        ax.scatter(1, 0, marker="o", s=150, color="black")
        ax.scatter(-1, 0, marker="o", s=150, color="blue")
        ax.set_title(r"$\mu > 0$", fontsize=19)

plt.show()

ポアンカレ・アンドロノフ・ホップ分岐

ヤコビ行列の1組の複素共役固有値が純虚数になる場合を考える。2次元ベクトル場

\begin{cases} \dot{x} = \mu x - \omega y - x(x^2 + y^2) \\ \dot{y} = \mu y + \omega x - y(x^2 + y^2) \end{cases}

を考える。極座標変換 (x, y) = (r\cos\theta, r\sin\theta) をすると、

\begin{cases} \dot{r} = r(\mu - r^2) \\ \dot{\theta} = \omega \end{cases}

となる。平衡点 O におけるヤコビ行列は

A = \begin{pmatrix} \mu & -\omega \\ \omega & \mu \end{pmatrix}

\mu を変化させたときのベクトル場は次の特徴を持つ。

  • \mu < 0：平衡点 O は複素共役固有値 \mu \pm i\omega を持ち安定。
  • \mu = 0：平衡点 O は共役な純虚数固有値 \pm i\omega を持つ。
  • \mu > 0：平衡点 O は複素共役固有値 \mu \pm i\omega を持ち不安定。その周囲に、安定な周回軌道をもつ。

このように、パラメータの変化により安定平衡点が不安定になり、その周囲に安定な周回軌道が生じるような分岐をポアンカレ・アンドロノフ・ホップ分岐という。

pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp


def f(t, X, mu):
    x, y = X
    omega = 5
    dydt = [
        mu * x - omega * y - x * (x**2 + y**2),
        mu * y + omega * x - y * (x**2 + y**2),
    ]
    return dydt


t_span = (0, 20)
t_eval = np.linspace(t_span[0], t_span[1], 2000)

initial_conditions_lists = [
    [
        [5, -5],
    ],
    [
        [5, -5],
    ],
    [
        [5, -5],
        [0, 0.1],
    ],
]
mus = [-0.5, 0, 10]

fig, axs = plt.subplots(1, 3, figsize=(18, 6))

for i, mu in enumerate(mus):
    ax = axs[i]

    for initial_conditions in initial_conditions_lists[i]:
        sol = solve_ivp(f, t_span, initial_conditions, args=(mu,), t_eval=t_eval)
        ax.plot(sol.y[0], sol.y[1], color="black")

        idx = 20
        ax.annotate(
            "",
            xy=(sol.y[0][idx], sol.y[1][idx]),
            xytext=(sol.y[0][idx - 1], sol.y[1][idx - 1]),
            arrowprops=dict(arrowstyle="->", color="black", mutation_scale=30),
        )

    ax.grid(True)
    ax.set_xlim(-5, 5)
    ax.set_ylim(-5, 5)
    ax.set_xlabel(r"$x$", fontsize=16)
    ax.set_ylabel(r"$y$", fontsize=16)
    if i == 0:
        ax.set_title(r"$\mu < 0$", fontsize=19)
    elif i == 1:
        ax.set_title(r"$\mu = 0$", fontsize=19)
    elif i == 2:
        ax.set_title(r"$\mu > 0$", fontsize=19)

plt.show()

5. 写像の周期点の分岐

パラメータ \mu \in \mathbb{R}^p をもつ自律系写像

\vec{x} \mapsto f(\vec{x}, \mu), \quad \vec{x} \in \mathbb{R}^n

を考える。\mu = \mu_0 のとき、\vec{x} = \vec{x}_0 が不動点（または固定点）であるとする。

f(\vec{x}_0, \mu_0) = \vec{x}_0

ベクトル場と同様に不動点 \vec{x}_0 からの変分 \xi \in \mathbb{R}^n についての方程式を立てて1次近似すると、以下の線形写像が得られる。

\begin{align*} &\xi \mapsto A\xi, \quad \xi \in \mathbb{R}^n, \\ &A = D_{\vec{x}} f(\vec{x}_0, \mu) = \left. \frac{\partial f}{\partial \vec{x}} \right|_{\vec{x}(t) = \vec{x}_0} = \left( \left. \frac{\partial f_i}{\partial x_j} \right|_{\vec{x}(t) = \vec{x}_0} \right)_{1 \leq i,j \leq n} \end{align*}

ヤコビ行列 A のどの固有値も単位円 S = \{ \lambda \in \mathbb{C} | |\lambda| = 1 \} 上にないとき、不動点は双曲型であるという。A の固有値すべてが単位円の内側にあるとき不動点は安定であり、また少なくとも1つの固有値が単位円の外側にあるとき不動点は不安定である。

写像 f の l 回合成写像を f^l と表す。f^{m}（1\leq m < l）では不動点ではなく、f^l で初めて不動点となる点を l 周期点という。

f^l(\vec{l}, \mu) = \vec{l}, \quad f^m (\vec{l}, \mu) \ne \vec{l} \quad (1\leq m < l)

f の周期点の分岐は f^l の不動点分岐を調べたらよい。ベクトル場と同様に \mu = 0 のとき、原点に非双曲型不動点をもつ場合を考える。

1次元写像の周期倍分岐

サドル・ノード分岐、トランスクリティカル分岐、ピッチフォーク分岐はベクトル場と同様に生じる。ここでは、周期倍分岐という2周期点が発生する分岐を説明する。

1次元写像

x \mapsto f(x, \mu) = -x -\mu x + x^3, \quad x \in \mathbb{R},\, \mu \in \mathbb{R}

を考える。\mu を変化させると、この写像は次のような変化をする。

  • \mu < 0 かつ |\mu| \ll 1：不動点 O は固有値 -1 - \mu を持つ。|-1 - \mu| < 1 より安定。
  • \mu = 0：不動点 O は固有値 -1 を持つ。
  • \mu > 0 かつ |\mu| \ll 1：不動点 O は固有値 -1 - \mu を持つ。|-1 - \mu| > 1 より不安定。2周期点 P^\pm = \pm \sqrt{\mu} が存在し安定。

2周期点については、

\begin{align*} f(\sqrt{\mu}, \mu) &= -\sqrt{\mu} - \mu \sqrt{\mu} + \mu \sqrt{\mu} = -\sqrt{\mu} \\ f(-\sqrt{\mu}, \mu) &= \sqrt{\mu} + \mu \sqrt{\mu} - \mu \sqrt{\mu} = \sqrt{\mu} \end{align*}

であることからわかる。また、

D_x(f^2)(\pm\sqrt{\mu},\mu) = f_x(\mp\sqrt{\mu},\mu)f_x(\pm\sqrt{\mu},\mu) = (-1 + 2\mu)^2 < 1

なので2周期点は安定である。

pythonプログラム
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.patches as patches

xs = np.linspace(-1, 1, 100)
mus = [-0.1, 0, 0.1]
init_xss = [[0.5], [0.5], [0.5]]

fig, axs = plt.subplots(1, 3, figsize=(18, 6))

for i, mu in enumerate(mus):
    ax = axs[i]
    fs = -xs - mu * xs + xs**3
    ax.plot(xs, fs, linewidth=1.5, color="red")
    ax.plot(xs, xs, color="black", linewidth=1.0)
    ax.plot(xs, -xs, color="black", linewidth=1.0)
    ax.axhline(0, color="black", linewidth=0.7)
    ax.axvline(0, color="black", linewidth=0.7)

    for init_x in init_xss[i]:
        x = init_x
        for _ in range(15):
            y = -x - mu * x + x**3
            ax.plot([x, x], [x, y], color="black")
            ax.plot([x, y], [y, y], color="black")
            arrow = patches.FancyArrowPatch(
                (x, x), (x, y), mutation_scale=15, color="black", arrowstyle="->"
            )
            ax.add_patch(arrow)
            arrow = patches.FancyArrowPatch(
                (x, y), (y, y), mutation_scale=15, color="black", arrowstyle="->"
            )
            ax.add_patch(arrow)
            x = y

    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.set_title(rf"$\mu = {mu}$", fontsize=19)
    ax.set_xlabel(r"$x$", fontsize=16)
    ax.set_ylabel(r"$f(x,\mu)$", fontsize=16)
    ax.grid(True)

plt.tight_layout()
plt.show()

2次元写像

2次元写像

\begin{align*} &\vec{x} \mapsto f(\vec{x}, \mu) = \left(f_1(x, y, \mu), f_2(x,y,\mu)\right)^T, \\ &\vec{x} = (x, y)^T \in \mathbb{R}^2, \quad \mu \in \mathbb{R} \end{align*}

の分岐を考える。1次元と同様に \mu = 0 のとき \vec{x} = \vec{0} に非双曲型不動点を持つ場合を調べる。ヤコビ行列

A = \begin{pmatrix} (f_1)_x & (f_1)_y \\ (f_2)_x & (f_2)_y \end{pmatrix}

の固有値によって分岐が決まる。

ヤコビ行列が実固有値 \lambda_1, \lambda_2 を持ち |\lambda_1| \ne 1 とすると、原点が非双曲型不動点となるのは \lambda_2 = 1 または \lambda_2 = -1 のときである。

  • \lambda_2 = 1：サドルノード分岐。拘束条件を課すとトランスクリティカル分岐、ピッチフォーク分岐。
  • \lambda_2 = -1：周期倍分岐

現象としては1次元と変わらず図も煩雑なので、これらの図は省略する（参考文献に分岐イメージ図がある）。

ナイマルク・サッカー分岐

ヤコビ行列が絶対値1の複素共役固有値をもつ場合、ナイマルク・サッカー分岐が生じる。2次元写像に極座標変換を施したとき

\begin{align*} &\begin{pmatrix} r \\ \theta \end{pmatrix} \mapsto \begin{pmatrix} g(r) \\ h(r, \theta) \end{pmatrix} = \begin{pmatrix} r + d \mu r + a r^3 \\ \theta + c_0 + c_1 \mu + b r^2 \end{pmatrix} \\ &a, b, c_0, c_1, d : \text{const.} \end{align*}

で与えられる写像を考える。g(0) = 0 より、原点は不動点である。ヤコビ行列は

A(\mu) = (1 + d\mu) \begin{pmatrix} \cos(c_0 + c_1 \mu) & -\sin(c_0 + c_1 \mu) \\ \sin(c_0 + c_1 \mu) & \cos(c_0 + c_1 \mu) \end{pmatrix}

であり、固有値は

(1 + d\mu) \exp \left( \pm(c_0 + c_1 \mu)i \right)

となる。d > 0, a < 0 のとき、この写像は次のような挙動をする。

  • \mu < 0 かつ |\mu| \ll 1：原点に固有値 (1 + d\mu)\exp(\pm(c_0 + c_1\mu)i) を持つ安定不動点が存在する。
  • \mu = 0：原点に固有値 \exp(\pm c_0 i) を持つ不動点をもつ。
  • \mu > 0 かつ |\mu| \ll 1：原点に固有値 (1 + d\mu)\exp(\pm(c_0 + c_1\mu)i) を持つ不安定不動点が存在する。その周囲に半径 r = \sqrt{-d\mu/a} の不変円を持つ。

このように安定不動点がパラメータの変化に伴って不安定化し、その周囲に安定な不変円が発生する分岐をナイマルク・サッカー分岐という。

pythonプログラム
import matplotlib.pyplot as plt
import numpy as np


a = -0.1
b = 0.01
c0 = 0.2
c1 = 0
d = 1


def g(r, mu):
    return r + d * mu * r + a * r**3


rs = np.linspace(-4, 4, 1000)
mus = [-0.1, 0, 0.1]

fig, axs = plt.subplots(1, 3, figsize=(18, 6))

for i, mu in enumerate(mus):
    ax = axs[i]
    gs = g(rs, mu)

    ax.plot(rs, gs, linewidth=1.5, color="red")
    ax.plot(rs, rs, color="black", linewidth=1.0)
    ax.axhline(0, color="black", linewidth=0.7)
    ax.axvline(0, color="black", linewidth=0.7)

    ax.set_xlim(-4, 4)
    ax.set_ylim(-4, 4)
    ax.set_title(rf"$\mu = {mu}$, d > 0, a < 0", fontsize=19)
    ax.set_xlabel(r"$r$", fontsize=16)
    ax.set_ylabel(r"$g(r)$", fontsize=16)
    ax.grid(True)

plt.tight_layout()
plt.show()

import matplotlib.pyplot as plt
import numpy as np


a = -0.1
b = 0.01
c0 = 0.2
c1 = 0
d = 1


def g(r, mu):
    return r + d * mu * r + a * r**3


def h(r, theta, mu):
    return theta + c0 + c1 * mu + b * r**2


mus = [-0.1, 0, 0.1]

fig, axs = plt.subplots(1, 3, figsize=(18, 6))

for i, mu in enumerate(mus):
    ax = axs[i]

    r0 = 0.7
    theta0 = 0
    x0 = r0 * np.cos(theta0)
    y0 = r0 * np.sin(theta0)
    ax.scatter(x0, y0, marker="o", color="blue")

    for _ in range(100):
        r1 = g(r0, mu)
        theta1 = h(r0, theta0, mu)
        x1 = r1 * np.cos(theta1)
        y1 = r1 * np.sin(theta1)
        ax.scatter(x1, y1, marker="o", color="blue")
        ax.annotate(
            "",
            xy=(x1, y1),
            xytext=(x0, y0),
            arrowprops=dict(arrowstyle="->", color="black"),
        )
        x0 = x1
        y0 = y1
        r0 = r1
        theta0 = theta1

    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.set_title(rf"$\mu = {mu}$, d > 0, a < 0", fontsize=19)
    ax.set_xlabel(r"$x$", fontsize=16)
    ax.set_ylabel(r"$y$", fontsize=16)
    ax.grid(True)

plt.tight_layout()
plt.show()


参考文献

GitHubで編集を提案

Discussion