はじめに
量子位相推定は,ユニタリ行列 U とその固有状態 \ket{u} が与えられたときに,その固有値 e^{2 \pi i \phi} の \phi を推定するアルゴリズムです.つまり,次の式を満たす \phi を求めるということです.
\begin{equation*}
U \ket{u} = e^{2 \pi i \phi} \ket{u}
\end{equation*}
このアルゴリズムは,Shor のアルゴリズムや量子数え上げなどで重要な役割を果たしています.
この記事では,逆量子フーリエ変換を利用した Kitaev の量子位相推定を説明します.量子フーリエ変換については 量子フーリエ変換のメモ に書いたので,そちらをご覧ください.
量子位相推定
U の固有値は e^{2 \pi i \phi} = \cos (2 \pi \phi) + i \sin (2 \pi \phi) という形なので,0 \leq 2 \pi \phi < 2\pi,すなわち 0 \leq \phi < 1 と仮定しても一般性を失いません.このことから,\phi を n 桁の 2 進数の小数 \phi = 0.j_1 j_2 \cdots j_n とします.n は基本的に未知なので,適当な精度で仮定します.
初期状態を \ket{0}^{\otimes n}\ket{u} とします.まず,\ket{0}^{\otimes n} に H^{\otimes n} を作用させます.
\frac{1}{2^{n/2}} (\ket{0} + \ket{1})^{\otimes n} \ket{u}
次に,k 番目の補助量子ビットを制御ビットとして,固有状態 \ket{u} に U^{2^{k-1}} を作用させます.
\begin{align*}
\frac{1}{\sqrt{2}} \left(\ket{0} \otimes \ket{u} + \ket{1} \otimes U^{2^{k-1}} \ket{u}\right) &= \frac{1}{\sqrt{2}} \left(\ket{0} \otimes \ket{u} + \ket{1} \otimes \left(e^{2\pi i \phi}\right)^{2^{k-1}} \ket{u}\right) \\
&= \frac{1}{\sqrt{2}} \left(\ket{0} + e^{2 \pi i(2^{k-1} \phi)} \ket{1}\right) \otimes \ket{u}
\end{align*}
2^{k-1} \phi に \phi = 0.j_1 j_2 \cdots j_n を代入すると,
\begin{align*}
2^{k-1} \phi = 2^{k-1} 0.j_1 j_2 \cdots j_n = j_1 j_2 \cdots j_{k-1} . j_{k} j_{k+1} \cdots j_n
\end{align*}
となります.オイラーの公式より,2^{k-1} \phi の整数部分は無視できるため,さきほどの式は次のように変形できます.
\begin{align*}
\frac{1}{\sqrt{2}} \left(\ket{0} + e^{2 \pi i(2^{k-1} \phi)} \ket{1}\right) \otimes \ket{u} &= \frac{1}{\sqrt{2}} \left(\ket{0} + e^{2 \pi i 0.j_{k}j_{k+1}\cdots j_n} \ket{1}\right) \otimes \ket{u}
\end{align*}
これをすべての 1 \leq k \leq n について作用させます.
\begin{align*}
\frac{1}{2^{n/2}} (\ket{0} + e^{2\pi i 0.j_1 j_2 \cdots j_n} \ket{1}) \otimes (\ket{0} + e^{2 \pi i 0.j_2 \cdots j_n}\ket{1}) \otimes \cdots \otimes (\ket{0} + e^{2 \pi i 0.j_n}\ket{1}) \otimes \ket{u}
\end{align*}
この状態は量子フーリエ変換の式と同じ形です.よって,補助量子ビットに対して,逆量子フーリエ変換を作用させると \ket{j_1 j_2 \cdots j_n} が得られます.最後に,補助量子ビットを測定すると \phi が求まります.
固有状態が未知の場合
ここまで,固有状態 \ket{u} が既知の場合を想定していましたが,未知の場合も考えられます.実際,Shor のアルゴリズム中では固有状態は未知です.
そこで,今度は一般の状態 \ket{\psi} を入力とします.\ket{\psi} は,U の固有値 e^{2\pi i \phi _k} に対応する固有状態 \ket{u_k} を用いて展開できます.
\ket{\psi} = \sum_{k} a_k \ket{u_k}
\ket{u} を \ket{\psi} に置き換えると,初期状態は次のようになります.
\ket{0}^{\otimes n} \ket{\psi} = \sum_{k} a_k \ket{0}^{\otimes n} \ket{u_k}
そのため,\ket{\psi} に量子位相推定をすると,\ket{\phi _k}\ket{u_k} の重ね合わせ状態が得られます.
\sum_{k} a_k \ket{\phi _k} \ket{u_k}
後は測定することで,いずれかの固有状態 \ket{u_k} とそれに対応した \ket{\phi _k} が得られます.
おまけ
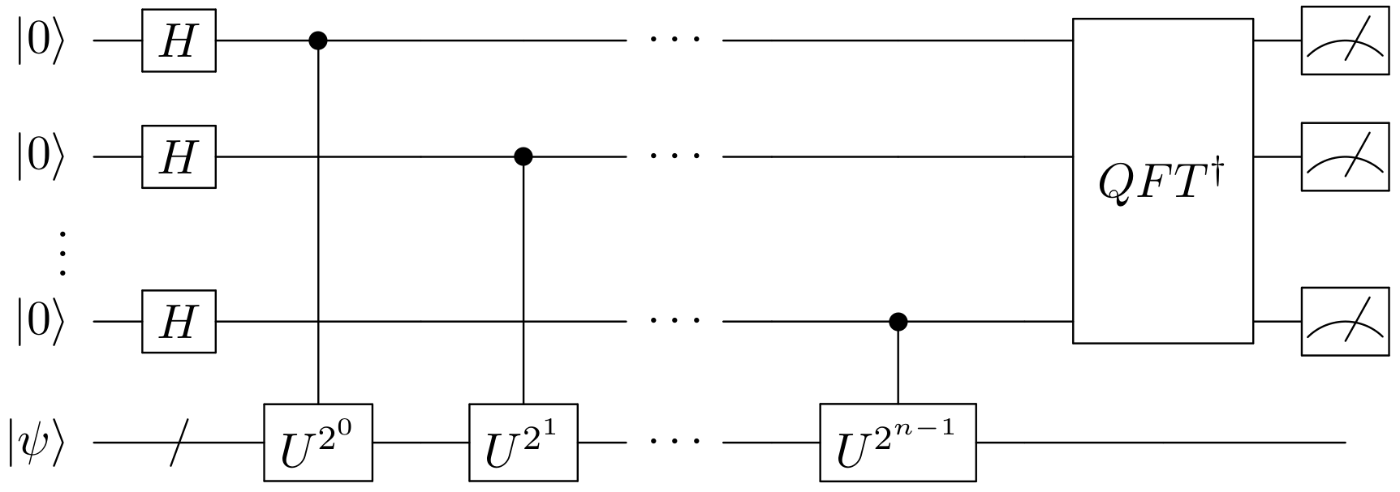
量子位相推定の量子回路の tex ファイルを置いておきます.
qpe.tex
\documentclass[uplatex]{jsarticle}
\usepackage{braket}
\usepackage{qcircuit}
\pagestyle{empty}
\begin{document}
\Qcircuit @C=1em @R=1em {
\lstick{\ket{0}} & \gate{H} & \ctrl{4} & \qw & \qw & \qw & \cdots & & \qw & \qw & \qw & \multigate{3}{QFT^\dag} & \meter \\
\lstick{\ket{0}} & \gate{H} & \qw & \qw & \ctrl{3} & \qw & \cdots & & \qw & \qw & \qw & \ghost{QFT^\dag} & \meter \\
\lstick{\vdots} \\
\lstick{\ket{0}} & \gate{H} & \qw & \qw & \qw & \qw & \cdots & & \qw & \ctrl{1} & \qw & \ghost{QFT^\dag} & \meter \\
\lstick{\ket{\psi}} & \qw {/} & \gate{U^{2^0}} & \qw & \gate{U^{2^1}} & \qw & \cdots & & \qw & \gate{U^{2^{n-1}}} & \qw & \qw & \qw \\
}
\end{document}

Discussion