標準偏差ペアを用いたマハラノビス距離の欠損値補完法

※約一年ほど前に仕事で思いつたことを残しておきます。

概要

マハラノビス距離における欠損値の扱いについて、平均値と標準偏差を用いた一つの単変量補完法を紹介します。
単純に欠損値を平均値で補完する場合、標本データの分散・共分散は欠損値のないデータと比べて過小評価されたり、試験データは異常検知において正常側に偏ったりする問題があります。
本記事の標準偏差ペアを用いる手法は、標本データの分散が過小評価されることを回避し、試験データが正常側に偏り過ぎることを回避します。
最初にマハラノビス距離の定義をした上で、標準偏差ペアを用いた補完法のアイデアを説明します。

マハラノビス距離の定義

分散共分散行列

$$\bm X = \begin{bmatrix} x^1_1 & x^1_2 & \cdots & x^1_K \\ x^2_1 & x^2_2 & \cdots & x^2_K \\ \vdots & \vdots & \ddots & \vdots \\ x^N_1 & x^N_2 & \cdots & x^N_K \\ \end{bmatrix}$$

$$\overline{\bm x} = \frac{1}{N} {\bm 1}_N {\bm X}$$

$$\bm 1_N = \begin{bmatrix} 1 & 1 & \cdots & 1 \\ \end{bmatrix}$$

$$\overline {\bm X} = \begin{bmatrix} \overline{\bm x} \\ \overline{\bm x} \\ \vdots \\ \overline{\bm x} \\ \end{bmatrix}$$

$$X_{\overline {\bm x}} = \bm X - \overline {\bm X}$$

$$\bm V = \frac{1}{N} \bm X_{\overline {\bm x}}^T \bm X_{\overline {\bm x}}$$

• $\bm X$: 標本データ
• $N$: 標本データの数
• $K$: 変量の数
• $\overline {\bm x}$: 変量毎の平均値
• $\bm X_{\overline {\bm x}}$: $\overline{\bm x}$で中心化した標本データ
• $\bm V$: 分散共分散行列

行列要素の右上の添字$n = 1 \dots N$は何番目のデータか、右下の添字$k = 1 \dots K$は何番目の変量かを示します。$\bm 1_N$は値がすべて1の要素数$N$のベクトルとします。$\bm X^T$は$\bm X$の転置行列とします。

マハラノビス距離

$$\bm Y = \begin{bmatrix} y^1_1 & y^1_2 & \cdots & y^1_K \\ y^2_1 & y^2_2 & \cdots & y^2_K \\ \vdots & \vdots & \ddots & \vdots \\ y^M_1 & y^M_2 & \cdots & y^M_K \\ \end{bmatrix}$$

$$\bm Y_{\overline{\bm x}} = \bm Y - \overline {\bm X}$$

$$\begin{aligned} \bm C &= \frac{1}{K} \bm Y_{\overline{\bm x}} \circ \bm Y_{\overline{\bm x}} \bm V^{-1} \\ &= \begin{bmatrix} c^1_1 & c^1_2 & \cdots & c^1_K \\ c^2_1 & c^2_2 & \cdots & c^2_K \\ \vdots & \vdots & \ddots & \vdots \\ c^M_1 & c^M_2 & \cdots & c^M_K \\ \end{bmatrix} \end{aligned}$$

$$\begin{aligned} {\bm d} &= \bm C {\bm 1}_K \\ &= \begin{bmatrix} d^1 \\ d^2 \\ \vdots \\ d^M \\ \end{bmatrix} \end{aligned}$$

$${\bm 1}_K = \begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \\ \end{bmatrix}$$

• $\bm Y$: 試験データ
• $M$: 試験データの数
• $\bm Y_{\overline {\bm x}}$: $\overline{\bm x}$で中心化した試験データ
• $\bm C$: 貢献度行列（と呼ぶことにします）
• $\bm d$: マハラノビス距離

$\bm V^{-1}$は$\bm V$の逆行列とします。$\circ$はアダマール積（要素積）とします。

マハラノビス距離の性質

$${\bm 1}_N {\bm d} = N, \text{if} ~ \bm Y = \bm X$$

試験データに標本データを用いる場合、マハラノビス距離の総和はデータ数に一致する（平均値は1になる）ことが知られています。

標準偏差ペアを用いた欠損値補完

アイデア

$$\bm X = \begin{bmatrix} x^1_1 & x^1_2 \\ \varnothing & x^2_2 \\ x^3_1 & \varnothing \\ \varnothing & \varnothing \\ \end{bmatrix}$$

$$\bm X^\sigma = \begin{bmatrix} x^1_1 & x^1_2 \\ x^1_1 & x^1_2 \\ x^1_1 & x^1_2 \\ x^1_1 & x^1_2 \\ \overline{x_1} + \sigma_1 & x^2_2 \\ \overline{x_1} + \sigma_1 & x^2_2 \\ \overline{x_1} - \sigma_1 & x^2_2 \\ \overline{x_1} - \sigma_1 & x^2_2 \\ x^3_1 & \overline{x_2} + \sigma_2 \\ x^3_1 & \overline{x_2} + \sigma_2 \\ x^3_1 & \overline{x_2} - \sigma_2 \\ x^3_1 & \overline{x_2} - \sigma_2 \\ \overline{x_1} + \sigma_1 & \overline{x_2} + \sigma_2 \\ \overline{x_1} + \sigma_1 & \overline{x_2} - \sigma_2 \\ \overline{x_1} - \sigma_1 & \overline{x_2} + \sigma_2 \\ \overline{x_1} - \sigma_1 & \overline{x_2} - \sigma_2 \\ \end{bmatrix}$$

• $\bm X$: 欠損値を含むデータ
• $\varnothing$: 欠損値
• $\bm X^\sigma$: 欠損値を補完したデータ
• $\overline{x_k}$: 変量$k$の平均値（欠損していない値から求めます）
• $\sigma_k$: 変量$k$の標準偏差（欠損していない値から求めます）

基本的なアイデアは、平均値と標準偏差ペアを用いて、1つの欠損値を含むデータから2つの補完データを作ることです。欠損値を含むデータが増えるので、他のデータはコピーを増やして均衡を取ります。この操作によって、各変量の平均値と分散を保ちつつ、欠損値を補うことができます。

欠損のある変量の数に対してデータ数が指数関数的に増加してしまう問題がありますが、これは計算式を整理すると解決されます。

計算式の整理

2変量のデータに1つだけ欠損値がある場合を考えます。
それから多変量で複数欠損がある一般形を考えます。

標本データの補完

$\bm X$はすでに中心化されているものとします。

欠損なしの場合

$$\bm X = \begin{bmatrix} x^1_1 & x^1_2 \\ x^2_1 & x^2_2 \\ \end{bmatrix}$$

$$\bm V = \frac{1}{2} \begin{bmatrix} (x^1_1)^2 + (x^2_1)^2 & x^1_1 x^1_2 + x^2_1 x^2_2 \\ x^1_1 x^1_2 + x^2_1 x^2_2 & (x^1_2)^2 + (x^2_2)^2 \\ \end{bmatrix}$$

平均値補完の場合

$$\bm X^0 = \begin{bmatrix} 0 & x^1_2 \\ x^2_1 & x^2_2 \\ \end{bmatrix}$$

$$\bm V^0 = \frac{1}{2} \begin{bmatrix} (x^2_1)^2 & x^2_1 x^2_2 \\ x^2_1 x^2_2 & (x^1_2)^2 + (x^2_2)^2 \\ \end{bmatrix}$$

標準偏差ペア補完の場合

$$\bm X^\sigma = \begin{bmatrix} \sigma_1 & x^1_2 \\ - \sigma_1 & x^1_2 \\ x^2_1 & x^2_2 \\ x^2_1 & x^2_2 \\ \end{bmatrix}$$

$$\begin{aligned} \bm V^\sigma &= \frac{1}{4} \begin{bmatrix} 2 (x^2_1)^2 + (\sigma_1)^2 + (- \sigma_1)^2 & 2 x^2_1 x^2_2 + x^1_2 (\sigma_1 - \sigma_1) \\ 2 x^2_1 x^2_2 + x^1_2 (\sigma_1 - \sigma_1) & 2 (x^1_2)^2 + 2 (x^2_2)^2 \\ \end{bmatrix} \\ &= \frac{1}{2} \begin{bmatrix} (x^2_1)^2 + \sigma_1^2 & x^2_1 x^2_2 \\ x^2_1 x^2_2 & (x^1_2)^2 + (x^2_2)^2 \\ \end{bmatrix} \end{aligned}$$

$\bm V^0$と$\bm V^\sigma$の差異を比較すると、$V^\sigma_{11} = V^0_{11} + \sigma_1^2$となっています。
一般化すると、$x_k$が一つ欠損している場合、$V^\sigma_{kk}$は$V^0_{kk}$に分散$\sigma_k^2$を足すことで求められます。

試験データの補完

$\bm Y$はすでに$\bm X$で中心化されているものとします。

欠損値なしの場合

$$\bm Y = \begin{bmatrix} y_1 & y_2 \\ \end{bmatrix}$$

$$\bm C = \frac{1}{2} \begin{bmatrix} {V^\sigma}^{-1}_{11} (y_1)^2 + {V^\sigma}^{-1}_{21} y_2 y_1 & {V^\sigma}^{-1}_{12} y_1 y_2 + {V^\sigma}^{-1}_{22} (y_2)^2\\ \end{bmatrix}$$

平均値補完の場合

$$\bm Y^0 = \begin{bmatrix} 0 & y_2 \\ \end{bmatrix}$$

$$\bm C^0 = \frac{1}{2} \begin{bmatrix} 0 & {V^\sigma}^{-1}_{22} (y_2)^2 \\ \end{bmatrix}$$

標準偏差ペア補完の場合

標準偏差ペアの貢献度をそれぞれ計算し、結果を足して2で割ることにします。
この操作はマハラノビス距離の性質（総和はデータ数に一致する）を保ちます。

$$\bm Y^{+\sigma} = \begin{bmatrix} \sigma_1 & y_2 \\ \end{bmatrix}$$

$$\bm Y^{-\sigma} = \begin{bmatrix} - \sigma_1 & y_2 \\ \end{bmatrix}$$

$$\bm C^{+\sigma} = \frac{1}{2} \begin{bmatrix} {V^\sigma}^{-1}_{11} (\sigma_1)^2 + {V^\sigma}^{-1}_{21} y_2 \sigma_1 & {V^\sigma}^{-1}_{12} \sigma_1 y_2 + {V^\sigma}^{-1}_{22} (y_2)^2 \\ \end{bmatrix}$$

$$\bm C^{- \sigma} = \frac{1}{2} \begin{bmatrix} {V^\sigma}^{-1}_{11} (-\sigma_1)^2 - {V^\sigma}^{-1}_{21} y_2 \sigma_1 & -{V^\sigma}^{-1}_{12} \sigma_1 y_2 + {V^\sigma}^{-1}_{22} (y_2)^2\\ \end{bmatrix}$$

$$\begin{aligned} \bm C^{\sigma} &= \frac{1}{2} (C^{+\sigma} + C^{-\sigma}) \\ &= \frac{1}{4} \begin{bmatrix} {V^\sigma}^{-1}_{11} ((\sigma_1)^2 + (-\sigma_1)^2) + {V^\sigma}^{-1}_{21} y_2 (\sigma_1 - \sigma_1) & {V^\sigma}^{-1}_{12} (\sigma_1 - \sigma_1) y_2 + 2 {V^\sigma}^{-1}_{22} (y_2)^2 \\ \end{bmatrix} \\ &= \frac{1}{2} \begin{bmatrix} {V^\sigma}^{-1}_{11} \sigma_1^2 & {V^\sigma}^{-1}_{22} (y_2)^2\\ \end{bmatrix} \end{aligned}$$

$\bm C^0$と$\bm C^\sigma$の差異を比較すると、$C^\sigma_1 = C^0_1 + {V^\sigma}_{11}^{-1} \sigma_1^2$となっています。
一般化すると、$y^m_k$が欠損している場合、${C^\sigma}^m_k$は${C^0}^m_k$に${V^\sigma}_{kk}^{-1}$と分散$\sigma_k^2$の積を足すことで求められます。

整理後の計算式

計算式はまとめると下記の式になります。

分散共分散行列

$$\bm V^\sigma = \bm V^0 + \text{diag}(\bm c \circ \bm \sigma^2)$$

$${\bm \sigma^2} = \begin{bmatrix} \sigma^2_1 & \sigma^2_2 & \cdots & \sigma^2_K \\ \end{bmatrix}$$

$${\bm c} = \begin{bmatrix} c_1 & c_2 & \cdots & c_K \\ \end{bmatrix}$$

• $\bm V^\sigma$: 標準偏差ペアを用いた分散共分散行列
• $\bm V^0$: 標本データの欠損値を平均値補完した場合の分散共分散行列
• $\text{diag}(\bm x)$: ベクトル$\bm x$を対角行列に変換
• $\bm \sigma^2$: 変量毎の分散（欠損していない値から求めます）
• $\bm c$: 変量毎の欠損値の数

マハラノビス距離

$${\bm d}^\sigma = \bm C^\sigma {\bm 1}_K$$

$$\bm C^\sigma = \bm C^0 + \bm F \circ \bm P$$

$$f^m_k = \begin{cases} 1 & \text{if} ~ y^m_k = \varnothing \\ 0 & \text{otherwise} \end{cases}$$

$$\begin{aligned} \bm p &= \text{Diag}({\bm V^\sigma}^{-1}) \circ \bm \sigma^2 \\ &= \begin{bmatrix} {V^\sigma}^{-1}_{11} \sigma_1^2 & {V^\sigma}^{-1}_{22} \sigma_2^2 & \dots & {V^\sigma}^{-1}_{KK} \sigma_K^2 \\ \end{bmatrix} \end{aligned}$$

$$\bm P = \begin{bmatrix} \bm p \\ \bm p \\ \vdots \\ \bm p \\ \end{bmatrix}$$

• $\bm d^\sigma$: 標準偏差ペアを用いたマハラノビス距離
• $\bm C^\sigma$: 標準偏差ペアを用いた貢献度行列
• $\bm C^0$: 試験データの欠損値を平均値補完した場合の貢献度行列
• $\bm F$: 欠損フラグ行列（と呼ぶことにします）
• $\text{Diag}(\bm X)$: 行列$\bm X$の対角成分を抽出

簡単な可視化

標準偏差ペアを用いた欠損値補完を行った一例を図示します。

マハラノビス距離の等高線

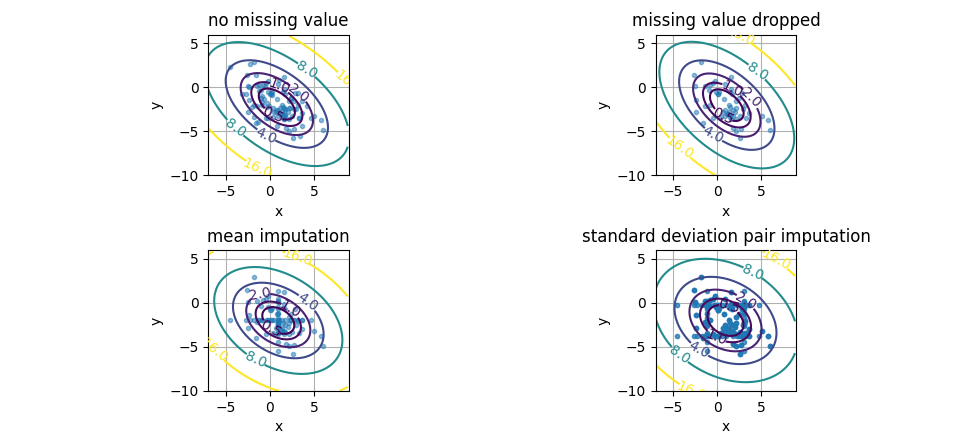
左上：欠損値なし、右上：欠損値を削除、
左下：平均値補完、右下：標準偏差ペアを用いた補完

標本データの生成条件は下記としました。

• 多変量正規分布による標本データ生成（multivariate_normal）
• 2変量
• ランダムに欠損（MCAR）
• 欠損率: 0.2
• データ数: 100

平均値補完では欠損値のあるデータは分布の中心に集まり、標準偏差ペアを用いた欠損値補完では中心から標準偏差だけ離れた位置に集まります。

まとめ

※あらゆるデータに対する計算機実験はまだできていません。

手法の特徴

• 計算量の少ない単変量補完
• 具体的な標本データが存在する
• 変量の分散を保つ補完
• 変量の共分散は小さくなる（欠損が多いほど標準化したユークリッド距離に近づく）
• 欠損値を含むデータが中心（平均値）に寄ることを回避する

その他考察

• 多クラス分類に使う場合、各クラスで欠損値の影響は平等に扱われるため、平均値補完で十分と思われます。
• 単クラス分類（異常検知）に使う場合、平均値補完と比べて、欠損値のある試験データが正常側に偏ってしまう現象を回避できると思われます。