私が考える数値計算ライブラリの問題点と私が数値計算ライブラリを開発する理由 (ポエム)

はじめに

この記事はポエムに近いですが，Zennは技術記事以外を書くのは規約違反ではないらしいのと，
私の考える現代の数値計算ライブラリの問題点を紹介することは，半分は技術的な内容かな？と思ったのでZennに書くことにしました．

私は会社で数値計算ライブラリの研究開発をしています．
私はかなり神経質かつ宗教的な信念を持って，数値計算ライブラリを開発することを研究と信じて続けているのですが，私が既存のライブラリにどういう問題点を感じていて，どういう宗教観で研究をしているのかについてあまり書いたことがないと思い立ち，ここに書くことにしました．

よくTwitterで他のソフトのコードを見てあれこれ言っていると，こいつは何が研究したいんだ．とか，こいつは何に不満があるんだ．と言われるんですが，この記事がその答えになると幸いです．

また，既存のライブラリの問題がこうだとか，こうしていくべきだとか偉そうに書きますが，それが合っているかどうかはわかりません．
あくまで私の宗教であり，いま現時点において私はこれが美しいと思っているという話なので，研究を進めていくうちに変わっていくこともあるかも知れません．

数値計算ライブラリの問題点

アムダールの法則

皆さんはアムダールの法則というのをご存知でしょうか？ Wikipediaを抜粋すると，

計算機の並列度を上げた場合に、並列化できない部分の存在、特にその割合が「ボトルネック」となることを示した法則である。

と書いてあります．簡単な図を使って雑に説明します．

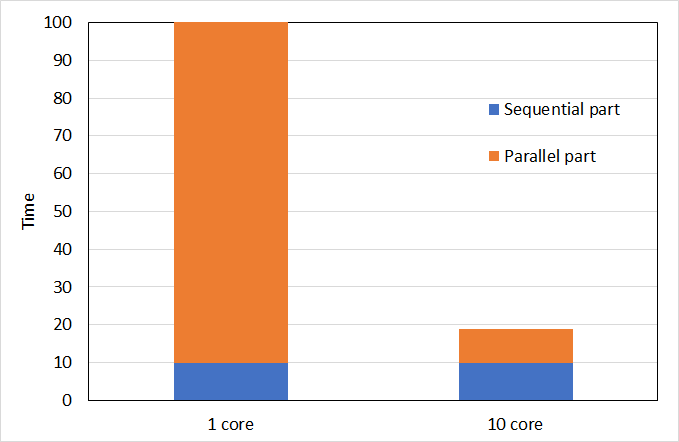
通常，並列化を行う際には時間がかかる計算から並列化を試みるのが自然です．1 coreの場合は，オレンジの部分が明らかに支配的 (time = 90)ですから，青い部分 (time = 10)は放っておいてオレンジの部分を高速化するのが普通です．
一方で10 coreになると90だったオレンジは9まで高速化され，並列化されずに放っておかれた青い部分のほうがむしろ時間がかかっています．
この場合，どこまで並列化してオレンジの部分を0に近づけたとしても，青い部分だけが残り，time = 10以下にはすることができません．

このように，プログラムの並列化されていない部分だけが残り続け，いくら並列化してもどこかでサチってしまうことを表した法則をアムダールの法則といいます．

10年ほど前であれば，CPUは多くても8コア，一般的には2~4コアくらいが主流で，多少並列化されていないところがあったとしても問題にはなりにくかったと言えます．
一方で最近のCPUのコア数は一般的なものでも新品デスクトップなら8コア程度，凄いものになるとRyzen Threadripper 3990Xなどは64コアを備えます．

既にシングルコアのプロセッサは新品では(少なくとも家電量販店には)販売されていないはずで，並列化されていないプログラムの意味は殆どないはずです．
100コア以上のCPUを想定してプログラムを書くことが想定される時代がすぐそこに来ていると思っています．

既にいくつかの領域では，2~4コアではなかった問題が64コアで顕在化してきていると捉えています (余談の章に書きました)．
このことから，例えどんなに細かく，今は問題にならない規模の処理であっても，並列化されていないということは10年後にユーザを苦しめると思っています．

アムダールの法則に基づく問題点と私の思想

続いて具体的な例を挙げていきます．
数値計算ライブラリとして代表的なBLAS, LAPACKは，多くの数値計算，線形代数において多くの時間を占める行列演算の関数を提供しています．
他の業界でもそうだと思いますが，このように時間のかかる / 複雑な処理はライブラリに任せるのが一般的です．

ざっくり書けば，ユーザは以下のようなプログラムを書くはずです．

// initialize
for(int i=0; i<N; i++){
    x[i] = rand();
}

// call library 
func(x);

このプログラムは初期化とライブラリコールに分かれています．ライブラリの内部が並列化されていれば，多くのプログラムは高速に動作するはずです．

しかしここでアムダールの法則を思い出します．プロセッサが毎年進歩していくと仮定すれば，毎年一番高いCPUに買い替えていけばライブラリコールは自然と速くなるはずですが，並列化されていない初期化の時間が縮まることはありません．
もちろんこの例は極端ですが，私は10年以内にこのような簡単なループですら並列化したくなると確信しています．

そして私は，どれだけ自分の書いたコードの計算時間が問題になったとしても，90%のユーザは並列化など試みないと確信しています．もっと言えば，時間を測って初期化が遅いのかライブラリコールが遅いのかすら検証することはないでしょう．
これは初学者などだけでなく，熟練した科学者にも当てはまると考えています．

この確信から，私はそもそもとしてユーザにライブラリコール以外のプログラムなど出来る限り書かせるべきではないと考えており，極論を言えば従来のボトルネック箇所のみの機能を持ったライブラリは10年後にユーザを苦しませる原因になると思っています．

そのためには必要な機能とAPIを定義し，ユーザのコードを置き換えていくことが必要です．
一気に高速なものを作ることは難しいはずです．しかしライブラリをupdateすれば高速になるのであれば，ユーザはついてきてくれるはずです．
初期のAPI設計および簡単なupdateの提供方法が課題になるでしょう (パッケージ管理システムのないプログラミング言語つらい．．．．)．

このことから，配列の初期化，入力，フォーマット変換，行列生成など，想定されうる様々な機能を出来る限り短く簡単なAPIとして策定，そして実装することが必要だと考えています．
配列に対する操作を全て検討することはおそらく不可能ですが，数値計算や機械学習などに対象を絞り，配列でなく行列やベクトルを対象とすれば，ユーザのニーズはgithubなどに十分に蓄積されているのではないかと考えています．

便利なライブラリはいっぱいあるが．．？

Pythonでいうところのnumpy, scipyや，数値計算に特化したJuliaなど，ユーザが殆ど処理を書かず，ライブラリコールだけでプログラムを開発できる環境は揃いつつあります．

一方でこれらの機能に対応したC/C++のライブラリは存在しません．
numpyのndarrayにはndarrayを操作するための膨大な機能が備わっていますが，BLAS/LAPACKにそんな機能はありません．

コードを見れば分かりますが，Rust, Julia, Pythonなどの近年モダンな言語における数値計算ライブラリは，BLAS/LAPACKにある関数はそれらを利用しますが，ない機能はそれぞれが独立して作り続けています (一部流用はもちろんある)．

特に疎行列に対するライブラリは完全に独立しており，中には並列化されていないものも存在します．そして，それはコードを見ないとわかりません (オープンソースなだけありがたいのですが)．

このようなそれぞれの環境でそれぞれの数値計算ライブラリが作られている状況は好ましくなく，ベースとなるBLAS/LAPACKに並ぶC/C++のレイヤで数値計算ライブラリをデザインし直す必要があると考えています．

(でもC/C++にはパッケージ管理システムが．．．．つらい．．．)

(余談) 実際にどういう時に問題になるの

私はKrylov部分空間法がメインのアプリケーションで，おそらく100個以上のCG法のコードを見てきましたが，その中の半分以上が内積やaxpyなどのベクトル計算や，初期化処理を並列化していませんでした．

多くの場合，疎行列は1行に100要素もないはずで，N行であれば疎行列ベクトル積の計算量は単純に2*100N以下です(キャッシュとか色々あるけど計算量だけ)．一方でベクトルに対する計算はCG法に8回含まれるので，2*8N回程度です．

つまり共役勾配法において疎行列ベクトル積が支配的と信じられていますが，計算量だけを見ると最大12.5倍しかありません．ベクトル計算を並列化せずに64コアのマシンなどで実行した場合，疎行列ベクトル積が支配的にならないことは十分にありえることだと思います．

さいごに

これまでデザインがどうだとか，置き換えていくべきだとか偉そうに書いてみましたが，私のデザインが合っているかどうかは全くわからないし，細部を見たら汚いデザインも大量にあります．

私は私の知る限り誰よりもプログラミングが嫌いです．ソフトウェアのいいところは，一度きちんとしたものを作ればそれを(ほぼ)コストなしに使い回せるところです．
私の抱く問題点は上に挙げたものであり，私の興味は，どのように数値計算ライブラリをデザインしたらよいのかです．

この記事をもって，少しでも問題点が誰かと共有できたら良いなと思っています．

最後に，私が会社で開発している数値計算ライブラリmonolishのリンクを張っておきますので，興味があったら見ていただいて，共感したらスターなどくれたら幸いです．

https://github.com/ricosjp/monolish