AtCoder Beginner Contest 261 E 解答までの思考

AtCoder Beginner Contest(ABC) 261のE問題を、コンテスト中に全テストケース正解(AC)することができました。ACになるまでに考えたことを書き残しておきます。

前提

ABCのコンテスト時間は90分のうち、本問題をACできたのが開始から73分43秒でした。
そのため、いくつか力技を含めてコンテスト中にACまで辿り着いた記録となります。
想定解をスムーズに導くより、コンテスト中の閃きの参考になればと思います。

筆者がGo言語で競技プログラミングに参加しているため、サンプルのコードはGo言語で記載しています。

問題

下記のページからの引用です。
https://atcoder.jp/contests/abc261/tasks/abc261_e

問題

問題文

変数 $X$ と、 $X$ の値を変更する $N$ 種類の操作があります。操作 $i$ は整数の組 $(T_i, A_i)$ で表され、意味は次の通りです。

• $T_i = 1$ のとき、 $X$ の値を $X and A_i$ に置き換える。
• $T_i = 2$ のとき、 $X$ の値を $X or A_i$ に置き換える。
• $T_i = 3$ のとき、 $X$ の値を $X xor A_i$ に置き換える。

変数 $X$ を値 $C$ で初期化した状態から、以下の処理を順に実行してください。

• 操作 $1$ を行い、操作後の $X$ の値を出力する。
• 続けて、操作 $1,2$ を順に行い、操作後の $X$ の値を出力する。
• 続けて、操作 $1,2,3$ を順に行い、操作後の $X$ の値を出力する。
• ⋮
• 続けて、操作 $1,2,…,N$ を順に行い、操作後の $X$ の値を出力する。

and,or,xor とは

非負整数 $A,B$ の $and,or,xor$ は、以下のように定義されます。

• $A and B$ を二進表記した際の $2^k (k \ge 0)$ の位の数は、 $A,B$ を二進表記した際の $2^k$ の位の数のうち両方が $1$ であれば $1$ 、そうでなければ $0$ である。
• $A or B$ を二進表記した際の $2^k (k \ge 0)$ の位の数は、 $A,B$ を二進表記した際の $2^k$ の位の数のうち少なくとも一方が $1$ であれば $1$ 、そうでなければ $0$ である。
• $A xor B$ を二進表記した際の $2^k (k \ge 0)$ の位の数は、 $A,B$ を二進表記した際の $2^k$ の位の数のうちちょうど一方が $1$ であれば $1$ 、そうでなければ $0$ である。

例えば、 $3 and 5=1$ 、 $3 or 5=7$ 、 $3 xor 5=6$ となります。

制約

• $1 \le N \le 2×10^5$
• $1 \le T_i \le 3$
• $0 \le A_i < 2^{30}$
• $0 \le C < 2^{30}$
• 入力に含まれる値は全て整数である

問題理解、計算量見積もり

まずは問題文と入力例を見ながら、解くべきことを理解していました。
こういったときは、紙に描きながら整理しています。入力例1を見ながら下図のように整理していました。

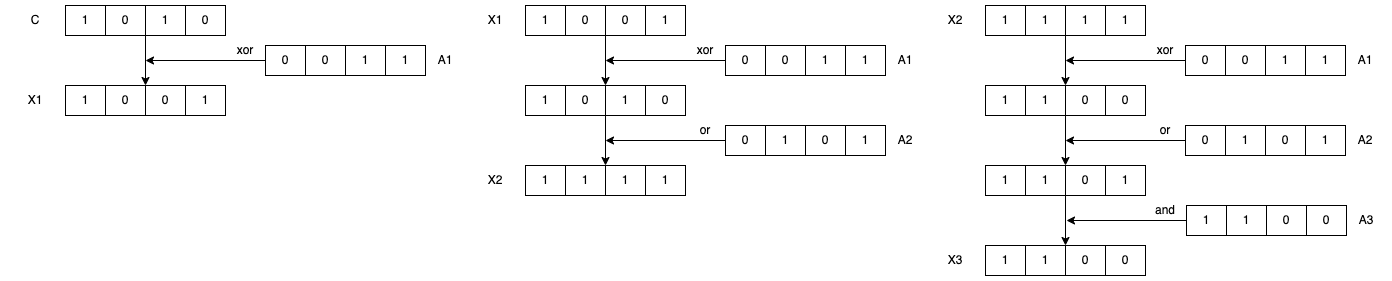
その後すぐに解法が浮かばなかったため、愚直に解くコードも書いてみました。

main.go

func solveHonestly(n, c int, t, a []int) (ans []int) {
	cc := c
	for i := 1; i <= n; i++ {
		for j := 0; j < i; j++ {
			switch t[j] {
			case 1:
				cc &= a[j]
			case 2:
				cc |= a[j]
			case 3:
				cc ^= a[j]
			}
		}
		ans = append(ans, cc)
	}
	return ans
}

入力例1、2くらいであれば問題無く出力が得られるので、自分の理解を確認したり、
後に出てきますテストにも流用しようとも考えていました。

計算量は $O(N^2)$ のため、このまま提出はできません。もう少し高速化を考える必要がありました。

高速化

bit演算は各桁数に注目する

知識の中から、この問題に合う解法を探してみました。
bitの演算は、各桁独立で計算が可能ですので、そのアプローチで考えてみました。
この知識は、例えば下記の過去問などから知識として持っていました。
https://atcoder.jp/contests/abc147/tasks/abc147_d

計算量は、 $N × (Cの桁数)$ で、遅くとも $O(10^6)$程度で間に合いそうな見積もりが出てきました。

操作は$xor$のみに限定して考察

ここから、 $i$ 番目の $X$ を $X_i$ として、 仮に操作を $xor$だけに注目してみました。問題の入力例1を、 $T_i = 3$としてみます。

3 10
3 3
3 5
3 12

この場合は下図のように $X_i$ 、 $A_i$ の $xor$ の累積から $X_i+1$が計算できます。

$and$ と $or$ の考察

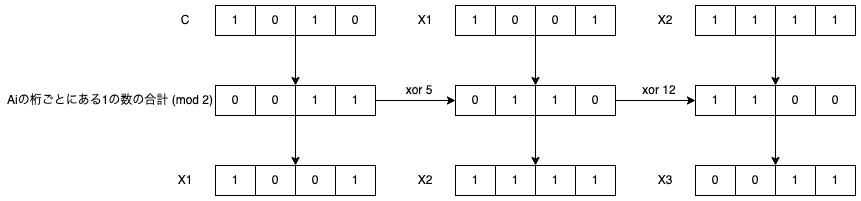
次に $and$、$or$についても、同じように各桁に注目して考察しました。

操作の各桁に注目するために、 $X_i$ 、 $A_i$ の下位 $j$ 桁目の値をそれぞれ $X_{ij}$ 、 $A_{ij}$ とします。 $A_{ij}$ が $0$ か $1$ の場合でそれぞれの値の変化を見ると下図のように変化することに整理できました。
そうすると、 $T_i=1$ かつ $A_{ij}=0$ と $T_i=2$ かつ $A_{ij}=1$ の場合は、それより前にどのような操作をしていようと、それぞれ $0$ 、 $1$になることがわかり、これを解答に利用できないかと考えられました。

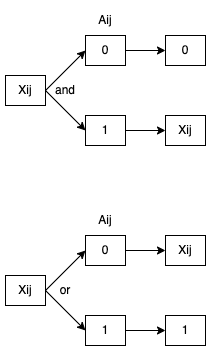
今までの考察のまとめ

$xor$ 、 $and$ 、 $or$ に関して考えたことをまとめると、

• $X_{i-1j}$ の値
• $T_i=1$ の中で $A_{i-1j}$ が $0$ である 最も大きい $i-1$
• $T_i=2$ の中で $A_{i-1j}$ が $1$ である 最も大きい $i-1$
  と
• 上記より後に操作する $T_i=3$ の中で $A_{i-1j}$ が $1$ である数
  を使うことで$X_i$ を計算できることにたどり着きました。

文字だけでは表現に自信がないため、入力例2を参考に絵にすると下図のようになります。
各桁ごとに、オレンジの部分のビットが $0$ か $1$ かと、緑の部分の $xor$ の累積を計算します。

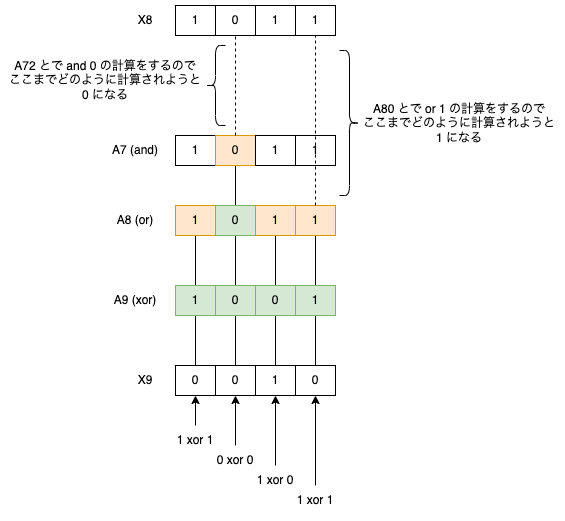
実装

今まで考察したことを実装にした関数がこちらです。

main.go

func solve(n, c int, t, a []int) []int {
	const maxBits = 30

	var andBits, orBits, xorBits [maxBits]int

	for j := 0; j < maxBits; j++ {
		andBits[j] = -1
		orBits[j] = -1
	}

	x := []int{c}
	for i := 0; i < n; i++ {
		//Aiの各桁を見て影響する値の更新
		for j := 0; j < maxBits; j++ {
			switch t[i] {
			case 1:
				if a[i]>>j&1 == 0 {
					andBits[j] = i
					xorBits[j] = 0
				}
			case 2:
				if a[i]>>j&1 > 0 {
					orBits[j] = i
					xorBits[j] = 0
				}
			case 3:
				if a[i]>>j&1 > 0 {
					xorBits[j]++
				}
			}
		}

		//影響する値とxorを見て次のXを計算
		var ncs [maxBits]int
		nextX := 0
		for j := 0; j < maxBits; j++ {
			if andBits[j] < 0 && orBits[j] < 0 {
				ncs[j] = x[i] >> j & 1
			} else if andBits[j] < orBits[j] {
				ncs[j] = 1
			} else if andBits[j] > orBits[j] {
				ncs[j] = 0
			}
			ncs[j] = (ncs[j] + xorBits[j]) % 2
			if ncs[j] == 1 {
				nextX |= 1 << j
			}
		}

		x = append(x, nextX)
	}

	// X0を除いて、X1~Xnまでを解答として返す
	return x[1:]
}

入出力を含めた全コードは下記にもあります。コンテスト中のコードは、不要な関数とかが記載されているものをそのまま提出していますので、同じ考えで改めて提出したものです。
https://atcoder.jp/contests/abc261/submissions/33494861

その他

作成しました解答の関数を、念のためローカルでも探索的にテストをしました。
$N \le 10^3$程度で、 制約の範囲で値をランダムに生成して$100〜1000$回程度なら数秒くらいで確認できました。
今回のように、最初に愚直に解くコードを書いてそこから高速化する場合にこういった確認もしています。特に、AtCoder Regular Contest(ARC)の問題を解く時にやっています。

main_test.go

package main

import (
	"fmt"
	"math/rand"
	"reflect"
	"testing"
	"time"
)

func Test_solve(t *testing.T) {
	type args struct {
		n int
		c int
		t []int
		a []int
	}
	type testCase struct {
		name string
		args args
		want []int
	}
	//再現性を維持したい場合は固定のシードを設定する
	rand.Seed(time.Now().UnixNano())
	var tests []testCase
	for i := 0; i < 1000; i++ {
		n := rand.Intn(2000)
		n++
		c := rand.Intn(1 << 30)
		var t, a []int
		for j := 0; j < n; j++ {
			ti := rand.Intn(3)
			ti++
			t = append(t, ti)
			a = append(a, rand.Intn(1<<30))
		}
		tests = append(tests, testCase{fmt.Sprintf("Case %03d", i+1), args{n, c, t, a}, solveHonestly(n, c, t, a)})
	}

	for _, tt := range tests {
		t.Run(tt.name, func(t *testing.T) {
			if got := solve(tt.args.n, tt.args.c, tt.args.t, tt.args.a); !reflect.DeepEqual(got, tt.want) {
				t.Errorf("solve() = %v, want %v", got, tt.want)
			}
		})
	}
}

実行例

$ go test
PASS
ok      github.com/hima398/go-programming-contest/atcoder/abc261/e      2.532s

最後に

ABC261のE問題に関するコンテスト中の思考をまとめてみました。
公式解説等を見ると、もっとシンプルに解く説明はいくつかあります。
今後F問題以降に十分な時間を残して、高いパフォーマンスを出すためには、
公式解説のような閃きが必要と感じました。まだまだ、精進すべきことはあると感じました。
https://atcoder.jp/contests/abc261/tasks/abc261_e/editorial