🦄

AtCoder Regular Contest 143 C 解答までの流れと嘘解法

2022/07/02に公開

競技プログラミングの精進として、AtCoder Regular Contest（ARC) 143 C問題、
Piles of Pebblesを解きました。全テストケース正解(AC)になるまでに考えたことと、
その途中で見つけた嘘解法を紹介します。

問題

下記のページからの引用です。

小石の山が $N$ 個あります．最初， $i$ 番目の山には $A_i$ 個の小石があります．

これらを用いて，高橋君と青木君がゲームをします．高橋君から始めて，交互に次の操作を行い，操作を行えなくなった方が負けとなります．

山を 1 つ以上選び，選んだそれぞれの山から，高橋君の操作の場合は $X$ 個ずつ，青木君の操作の場合は $Y$ 個ずつ小石を取り除く．ただし，小石の個数が足りない山を選ぶことはできない．
二人が最適に行動したとき，どちらがゲームに勝つかを求めてください.

値をシンプルにして二人の最適な行動を考える

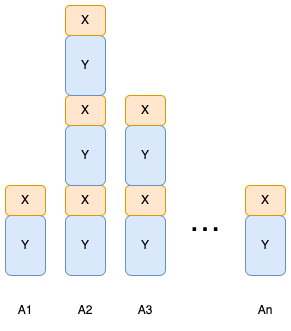
$A_i(1\le i\le N)$ から $X$ 個、 $Y$ 個ずつ石を取っていくので $A_i$ を $X+Y$ の倍数と考えてみました。

この状態であれば

先手がいくつか山を選んで $X$ 個の石を取る
後手が同じ山を選んで $Y$ 個の石を取る

ということを繰り返せば、先手がどの山からも石が取れなくなり後手が必勝ということがわかりました。

$A_i$ をより一般化する

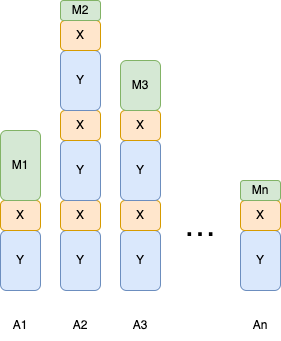
上で考えたシンプルな例を基に $A_i$ を一般化してみました。実際には $A_i$ を $X+Y$ で割った余り $M_i(1\le i\le N, 0 \le M_i\lt X+Y)$ があります。

改めて $M_i(1\le i\le N, 0\le M_i\lt X+Y)$ ですので

$M_i$ から取れる最後の石を取った方が必勝
各 $M_i$ からは先手、後手のどちらかしか石を取れないか、どちらも石を取れない

ここで何となく先手で $M_i$ から石を取れなければ負け、1つ以上の $M_i$ から石が取れれば勝ちそうな感触が掴めてきました。

嘘解法

上の感触をコード化してみましたら、、、ACになりました。

でも少し引っかかる点がありましたので、もう少し考察してみました。
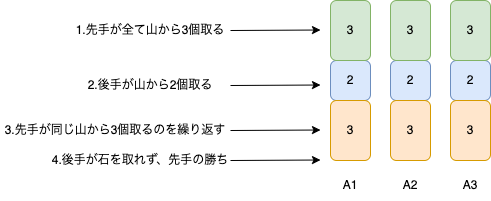
例えば、 $N=3, X=3, Y=2, A=\{8, 8, 8\}$ の場合は、下図のように先手が勝つ手がありますが、後手が勝つと判定されてしまいます。

# t1.txtは上記のテストケース
$ go run main.go < t1.txt
Second

改めて解法を提出

嘘解法は $X\gt Y$ のケースについて、考察が不十分と考えられました。
例えば、先手が $X$ 個石を取った後、先手が石を取れなかった山に $Y$ 個の石が残っている場合があります。

この考察を嘘解法でおかしかったケースも正しくなることも確認し、その他考慮漏れがないか
先手、後手それぞれどのような条件であれば勝てるかを整理しました。

$X$ 、 $Y$ の大小	先手	後手
$X\le Y$	$M_i$ から1つ以上の山から石が取れる	先手が $M_i$ から石を取れない
$X\gt Y$	$M_i$ から1つ以上の山から石が取れ、後手が石を取れない	先手が $M_i$ から石を取れないもしくは先手が石を取った後1つ以上の山から石が取れる

改めて提出してACになりました。

最後に

今回は精進ですので、それなりの時間をかけて考察をしました。
途中、嘘解法がありましたものの、ARCの問題でACに辿りついたときときは
AtCoder Beginner Contest(ABC)とは違った達成感がありました。
これがコンテスト中にできると、さらにそういった感触が味わえたり、レートの飛躍もできるかなと思います。
残念ながら、私はARCでは中々レートアップすることができないため、
コンテスト時間中にひらめくことが個人的な課題と思います。

問題

値をシンプルにして二人の最適な行動を考える

A_iをより一般化する

嘘解法

改めて解法を提出

最後に

Discussion

$A_i$ をより一般化する