Causal impactを調べてみた。
はじめに
これまで手持ちデータでPythonライブラリでCausal imactを使っていましたが、モデルの中身を調べず使っていたので、今回、論文や参考サイトなどで調べてみました。
Causal imactとは
時系列データについてキャンペーンやプロモーションなどの介入が売上やアクセス数などの指標にどのような影響を与えたか分析する因果推論の手法です。実測値と反実仮想(予測値)をベイズ推論を用いて効果を推定して効果量を推定します。後ほど少し触れますが、差の差分法(DiD)の時系列対応バージョン的なイメージです。GoogleがRパッケージを公表していますが、Pythonでも非公式ライブラリが利用できます。
Pythonライブラリをつかってみる
と書いてみましたが、PythonはCausalimact公式ライブラリがないようです。
いくつか非公式ライブラリがあるようですが、今回は、tfcausalimpactを使います。
- 時系列を仮定するためデータを観測データをトレンド+季節性としてランダムで値を生成します。
- 介入効果を確認するため介入後(n=200から)に一定範囲の効果量をランダムで加えています。
pip install tfcausalimpact==0.0.13
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from causalimpact import CausalImpact
# 観測データの生成
np.random.seed(42)
n = 300
# トレンド
true_trend = np.cumsum(np.random.normal(0, 0.5, size=n))
# 季節性
true_seasonal = 10 * np.sin(np.linspace(0, 3 * np.pi, n))
# 観測データ
y = true_trend + true_seasonal + np.random.normal(0, 0.5, size=n)
# n=200から介入
data = pd.DataFrame({'y': y, 'seasonal': true_seasonal})
data['intervention'] = 0
data.loc[200:, 'intervention'] = 1
# 日付インデックスを設定(仮の日付を使用)
data.index = pd.date_range(start='2023-01-01', periods=n, freq='D')
# 介入後の期間(介入効果仮定)にランダム値を追加
data.iloc[200:, data.columns.get_loc('y')] += np.random.uniform(3.0, 5.0, size=len(data.iloc[200:]))
# 介入前と介入後の期間設定
pre_period = [data.index[0], data.index[199]]
post_period = [data.index[200], data.index[-1]]
# CausalImpactの実行
ci = CausalImpact(data[['y', 'seasonal']], pre_period, post_period)
print(ci.summary(output='report'))
ci.plot()
ライブラリ出力結果
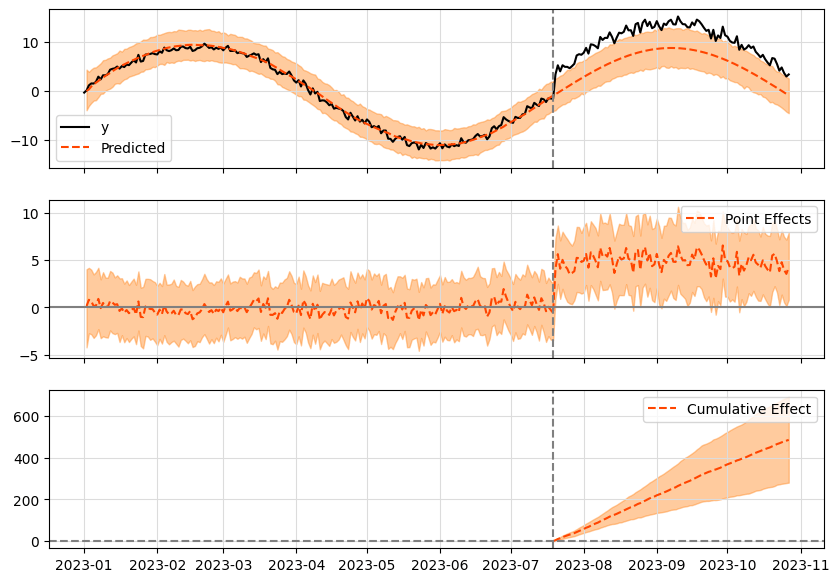
コード量も少なく簡単に使うことができます。
グラフの見方
- 1つ目のグラフ
Predict(予測値)=オレンジ線
介入以前のトレンドと季節値と同じ傾向で予測(反実仮想)されています。
y(観測値)=黒線
介入期間は、観測値yが増えています。 - 2つ目のグラフ
効果量=予測値-観測値 - 3つ目のグラフ
効果量の累積値
モデルの中身と工夫について
論文を読んでみる
Inferring causal impact using Bayesian structural time-series models
Causal imactモデルの概要
論文のうちモデルに関する内容は以下のことが書いてありました。
- DiDでは時間構造を扱えない
- 反実仮想データを推定して効果を推定
- 状態空間モデルを使用
- ベイズ構造時系列モデル ※信頼区間を設定
- 特徴量の選別(spike-and-slab)
このうちベイズ構造時系列モデルとspike-and-slabについて確認します。
ベイズ構造時系列モデル
ベイズ構造時系列モデル(Bayesian Structural Time-Series Model: BSTS)は、時系列データに対してベイズ推論を用い、トレンド、季節性、共変量(その他の外部変数)などの時系列パターンを捉えることができます。予測や推定に対する不確実性(信頼区間や予測区間)を考慮した確率的な予測ができます。
コード
# BSTSモデルの定義 (トレンド + 季節性)
import numpy as np
import pymc as pm
import arviz as az
import matplotlib.pyplot as plt
# データの生成
np.random.seed(42)
n = 50
# 観測値(ランダム)
true_trend = np.cumsum(np.random.normal(0, 0.2, size=n))
true_seasonal = 10 * np.sin(np.linspace(0, 5 * np.pi, n))
y = true_trend + true_seasonal + np.random.normal(0, 2.0, size=n)
# BSTSモデルの定義 (トレンド + 季節性)
with pm.Model() as model:
# トレンド
sigma_trend = pm.Exponential('sigma_trend', 0.2)
trend = pm.GaussianRandomWalk('trend', sigma=sigma_trend, shape=n)
# 季節性
sigma_seasonal = pm.Exponential('sigma_seasonal', 0.2)
seasonal = pm.GaussianRandomWalk('seasonal', sigma=sigma_seasonal, shape=n)
# トレンド + 季節性の合計を観測値として設定
total = pm.Deterministic('total', trend + seasonal)
# 観測
sigma_obs = pm.HalfNormal('sigma_obs', 20)
y_obs = pm.Normal('y_obs', mu=total, sigma=sigma_obs, observed=y)
# サンプリング
trace = pm.sample(2000, chains=4, tune=1000, target_accept=0.95, return_inferencedata=False)
# 結果のプロット
fig, ax = plt.subplots(figsize=(12, 6))
# 観測データのプロット
ax.plot(range(n), y, label='Observed Data', color='black', linewidth=1.5)
# トレンド + 季節性の合計の95%信頼区間を取得し、可視化
total_samples = trace['total']
total_hpd = az.hdi(total_samples, hdi_prob=0.95)
# 平均値とHPD(95%信頼区間)をプロット
total_mean = total_samples.mean(axis=0)
ax.plot(range(n), total_mean, label='Trend + Seasonal (Estimated)', color='green', linewidth=2)
ax.fill_between(range(n), total_hpd[:, 0], total_hpd[:, 1], color='purple', alpha=0.5, label='95% Confidence Interval')
# 縦軸の範囲を設定
ax.set_ylim(-20, 20)
# 凡例の設定
ax.legend()
ax.set_xlabel("Time")
ax.set_ylabel("Value")
ax.set_title("Time Series Data with BSTS Model Total Estimate and 95% Confidence Intervals")
plt.show()
ベイズ構造時系列モデル出力結果
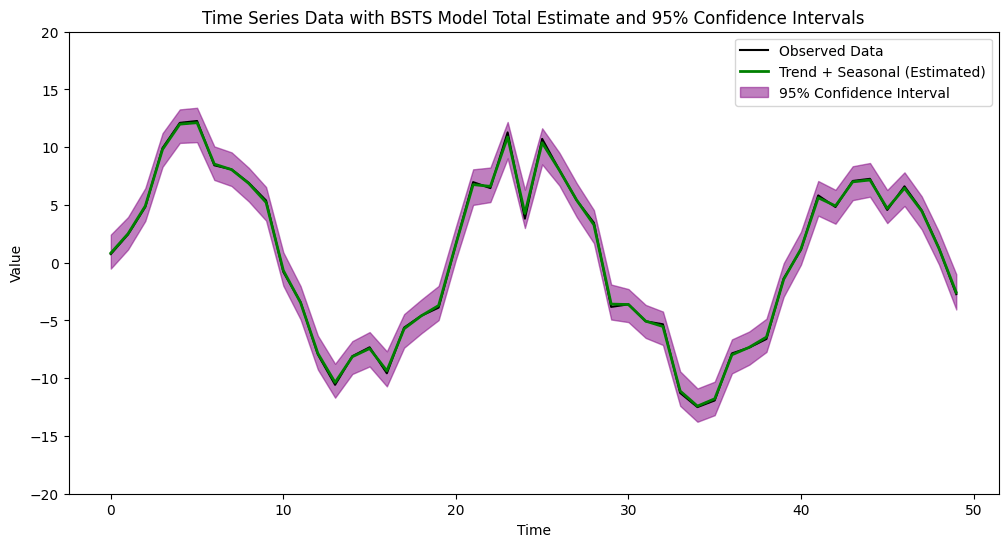
今回、シンプルなサンプリングなのでかなりフィットしています。
- 黒の線(Observed Data)
ランダム生成した観測データです。 - 緑の線(Trend + Seasonal (Estimated))
ベイズ構造時系列モデルが推定したトレンドと季節性の合計値です。 - 紫の帯(95% Confidence Interval)
95%の信頼区間です。このモデルの予測値がこの区間の範囲内に収まる確率が95%です。
spike-and-slab
論文には、特徴量選択についてSpike-and-Slab Priorのことが書かれています。
不要な特徴量が排除され、重要な特徴量を残します。
- Spike
不要な特徴量の係数をゼロにして排除する。 - Slab
残った(必要な)特徴量の係数をモデルに残す。
コード
import pymc as pm
import numpy as np
import matplotlib.pyplot as plt
# データの生成
np.random.seed(42)
n = 100
X = np.random.randn(n, 3)
true_beta = np.array([2, 0, -3])
y = X @ true_beta + np.random.randn(n)
# Spike-and-Slabモデルの定義とサンプリング
with pm.Model() as model:
# Spike-and-Slab prior
slab = pm.Normal('slab', mu=0, sigma=10, shape=3)
spike = pm.Bernoulli('spike', p=0.5, shape=3)
beta = pm.Deterministic('beta', slab * spike)
# モデル
sigma = pm.HalfNormal('sigma', sigma=1)
mu = pm.math.dot(X, beta)
y_obs = pm.Normal('y_obs', mu=mu, sigma=sigma, observed=y)
trace = pm.sample(2000, target_accept=0.99, return_inferencedata=True)
# 結果のプロット
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# スパイクとスラブの事前分布をプロット
x = np.linspace(-15, 15, 300)
for i in range(3):
# スラブ(正規分布)のみ
slab_pdf = norm.pdf(x, loc=0, scale=10)
axes[i].plot(x, slab_pdf, label='Slab (Normal)', color='blue')
# Spike≠0 のヒストグラム
axes[i].hist(trace.posterior['beta'].sel(chain=0, draw=slice(None))[i], bins=10, density=True, alpha=0.5, color='green')
axes[i].set_ylim(0, 0.5)
axes[i].set_title(f"Posterior Distribution of β[{i}] (Spike-and-Slab)")
axes[i].legend()
plt.tight_layout()
plt.show()
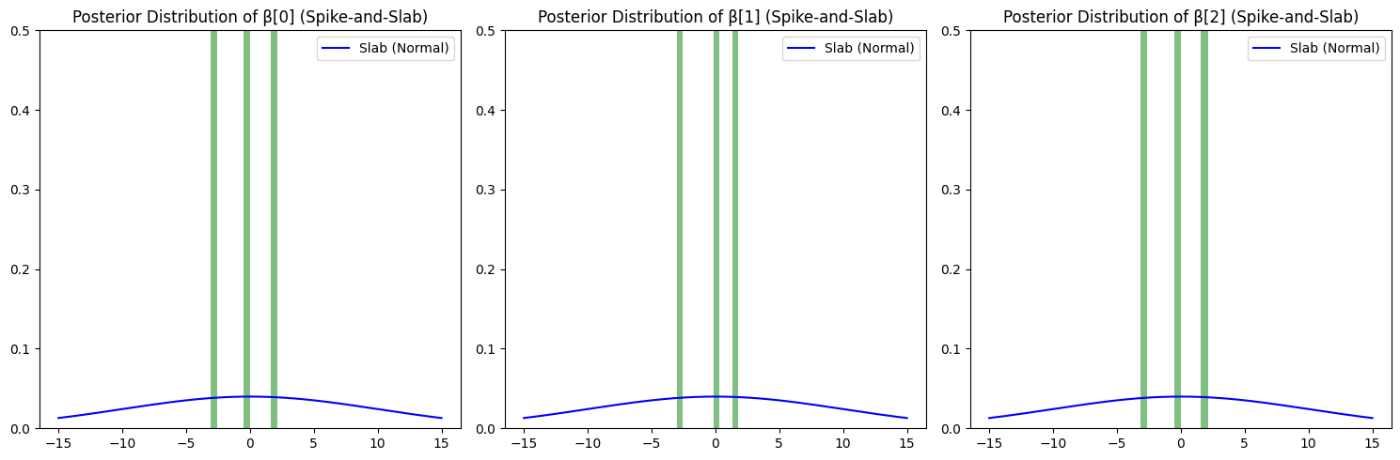
3変数に対し、spikeでベルヌーイ(0,1)を出力しています。
slabでは、正規分布からサンプリングしていて、その値をbeta内でspikeの0,1と掛け算し、特徴量を抽出します。
今回だと正規分布でサンプリングしているので、平均周辺の特徴量が多く抽出されます。
まとめ
Causal Impactがベイズ構造時系列モデルを使っていることは知っていましたが、Spike-and-Slabについては理解が浅かったです。今回はサンプルとして正規分布やベルヌーイ分布を使用していますが、他の分布を使う場合でも特徴量選択の仕組みが機能するということですね。Causal Impactのライブラリはコードがシンプルで、処理時間もそこまでかからないため、時系列データの因果推論を行う際、他のモデルと併せて試してみるのも良さそうです。
その他
- 静的回帰と動的回帰を使って効果量を推定している。
- 因果推論を行うので、交絡因子には注意
- 反実仮想データを生成するため多重共線性にも注意
参考
論文
Inferring causal impact using Bayesian structural time-series models
ブログ
{CausalImpact}を使う上での注意点を簡単にまとめてみた - 渋谷駅前で働くデータサイエンティストのブログ
スライド
Causal Impact -paper summary-
ライブラリ
Discussion