🔖
Rustで実装するZeroGrads: ブラックボックス関数に対して勾配法を適用

2024/07/16に公開
Rust
 TL;DRZeroGradsという解析微分を定義していない関数[1]に対して勾配法に似た最適化を行う新しいアルゴリズムの紹介。
Rust + candleライブラリでZeroGradsを実装して、簡単な高次元関数で効果的に機能するかの確認を行った。
Optunaなどのベイズ最適化と比較と使い分けの雑感を書きました。

 はじめに最適化問題は機械学習、コンピュータグラフィックス、工学設計など、多くの分野で重要な役割を果たしています。しかし、高次元の複雑な問題や勾配情報が直接利用できない場合、従来の最適化手法では効率的に解を見つけることが困難でした。
本記事では、この課題に取り組む新しいアプローチであるZeroGradsアルゴリズムの紹介を行い、実際にRust+candleで実装を行うことでその実装方法を紹介していきます。

 2. ZeroGradsアルゴリズムの概要
 ZeroGradsの特徴ZeroGradsは、SIGGRAPHで発表予定のMichael FischerとTobias Ritschelによって提案された最適化アルゴリズムです。

主な特徴は以下の通りです：

サロゲート関数:

最適化対象の関数の近似として、ニューラルネットワークなどのサロゲート関数を使用します。

局所的な学習:

現在のパラメータ周辺の局所的な領域でサロゲート関数を学習します。

スムージング:

目的関数に対してガウシアンカーネルによるスムージングを適用します。

効率的なサンプリング:

重要度サンプリングを用いて、サロゲート関数の勾配を推定します。
これらの特徴により、ZeroGradsは解析微分が定義されていない高次元の複雑な最適化問題に対して効果的に機能します。
論文中では主にCGのパラメータの最適化の実験などを行っています。


論文中のZeroGradsでBRDFを最適化する実験

 ZeroGradsの流れZeroGradsアルゴリズムの主な流れは以下の通りです：
初期化: パラメータとサロゲートモデルを初期化します。
サンプリング: 現在のパラメータ周辺でサンプルを生成します。
目的関数評価: サンプルに対して目的関数を評価します。
サロゲートモデル更新: サンプルと目的関数の評価結果を用いてサロゲートモデルを更新します。
パラメータ更新: サロゲートモデルの勾配を用いてパラメータを更新します。
繰り返し: 2-5のステップを収束するまで繰り返します。
この流れにより、直接勾配を計算できない関数に対しても、勾配法に似たアプローチで最適化を行うことができます。

 3. ZeroGradsのRust実装今回の実装では、Rustでcandleライブラリを利用して実装しています。

Rustで実装しているのは半分趣味で半分は再現性の高い実装にするためです。

 candleライブラリの特徴今回の実装では、RustでCandleライブラリを利用しています。
candleは機械学習ライブラリとして、以下のような特徴があります：
機械学習プラットフォーム Hugging Face の管理下のプロジェクト
pytorchライクなAPI:Rustの型システムとうまく付き合いながら、pytorchライクなAPIを利用できます。
マルチプラットフォーム対応:プラットフォームへの対応はかなり充実していて、MacOS上ではMetal版やCPU版でもAccelerate(Apple謹製のCPU向けの科学技術計算ライブラリ)を利用するモードがあります。
軽量設計:必要最小限の依存関係で構築されており、プロジェクトへの導入が容易です。
これにより、いろいろなプラットフォームでの再現性が高い実装になったと思っています。

 4. この実験コードの問題設定今回はZeroGradsが公開している例[2]に習って以下のような簡単な高次元関数を考えます。
 f(\bm{x}) = \sum_{i=1}^n{x_i} 実験では1000次元で行っています。

この関数をZeroGradsを利用して、最小化するというようなコードになります。
!この関数は明らかにx_iについて微分可能です。

今回はトイプログラムとしてこの関数を微分できないものと扱ってZeroGradsやベイズ最適化を適用していきます。

 コードの解説コードの全体はここに置いています。

https://github.com/higumachan/toy-zero-grads-rs

 サロゲートモデルの定義pub struct Proxy {
    pub model: Sequential,
}

impl Proxy {
    pub fn new(input_dim: usize, var_builder: VarBuilder) -> Result<Self> {
        let vb = var_builder;
        let model = seq()
            .add(linear(input_dim, 64, vb.pp("proxy/linear1"))?)
            .add(Activation::LeakyRelu(0.01))
            .add(linear(64, 64, vb.pp("proxy/linear2"))?)
            .add(Activation::LeakyRelu(0.01))
            .add(linear(64, 64, vb.pp("proxy/linear3"))?)
            .add(Activation::LeakyRelu(0.01))
            .add(linear(64, 1, vb.pp("proxy/out"))?)
            .add(Activation::LeakyRelu(0.01));
        Ok(Self { model })
    }

    pub fn forward(&self, x: &Tensor) -> Result<Tensor> {
        self.model.forward(x)
    }
}
このコードでは、サロゲートモデルとして4層のニューラルネットワークを定義しています。各層は64ユニットを持ち、活性化関数としてLeaky ReLUを使用しています。

 初期化    let device = Device::Cpu;
    let varmap = VarMap::new();
    let var_builder = VarBuilder::from_varmap(&varmap, DType::F32, &device);
    let ndim = 1000;
    let proxy = Proxy::new(ndim, var_builder)?;

    let mut param_varmap = VarMap::new();
    param_varmap
        .get(&[ndim], "x", Init::Const(0.0), DType::F32, &device)
        .unwrap();
    param_varmap
        .set_one("x", (Tensor::ones(&[ndim], DType::F32, &device)? * 100.0)?)
        .unwrap();

    let x = param_varmap.get(&[ndim], "x", Init::Const(0.0), DType::F32, &device)?;

    let mut nn_opt_params = ParamsAdamW::default();
    nn_opt_params.lr = 5e-1;
    let mut nn_opt = AdamW::new(param_varmap.all_vars(), nn_opt_params)?;
このコードでは以下の初期化を行っています：
デバイスの設定: Device::Cpuを使用して、CPUでの計算を指定しています。
変数マップの作成: VarMapを使って、モデルのパラメータを管理するための変数マップを作成します。
次元数の設定: ndim = 1000で、1,000次元の最適化問題を設定しています。
プロキシ（サロゲートモデル）の作成: Proxy::new()を使って、サロゲートモデルを初期化します。
最適化パラメータの初期化:
100.0で満たされたテンソルを作成します。
これにより、最適化の開始点を設定しています。
オプティマイザの設定:
AdamW最適化アルゴリズムを使用します。
学習率を0.5（5e-1）に設定しています。
この初期化プロセスにより、ZeroGradsアルゴリズムの実行に必要な全ての要素（サロゲートモデル、最適化パラメータ、オプティマイザ）が準備されます。高次元（1,000次元）の問題に対応できるよう設定されており、CPU上で効率的に計算を行うための準備が整えられています。

 最適化ループfor i in 0..100_00 {
    let start = Instant::now();
    let batchsize = 2;
    // outerの正規分布に従ってパラメータをずらすための乱数を取得
    let samples = Tensor::randn(0.0, sigma, &[batchsize, ndim], &device)?;

    let x_batched = x.expand(&[batchsize, ndim])?;

    // サロゲート関数を学習するためのパラメータを作成
    let xs = Tensor::cat(&[&(&x_batched + &samples)?, &(&x_batched - &samples)?], 0)?;

    // サロゲート関数を学習するためのパラメータに目的関数を実行した値を作成
    let fs = (0..xs.shape().dims()[0])
        .map(|i| objective(&xs.get(i).unwrap()))
        .collect::<Vec<f32>>();
    let fs_tensor = Tensor::from_vec(fs.clone(), &[fs.len()], &device)?;

    // サロゲート関数の更新
    for _ in 0..3 { 
        // サロゲート関数への入力を作成
        let xs_pert =
            (&xs - &Tensor::randn(0.0, 0.1 * sigma, &[batchsize * 2, ndim], &device)?)?;
        // サロゲート関数の出力を作成
        let nn_pred = proxy.forward(&xs_pert)?;
        // サロゲート関数と目的関数の出力のMSEを最小化するようにサロゲート関数のパラメータを更新する
        let p_loss = mse(&nn_pred.flatten_all().unwrap(), &fs_tensor)?;
        nn_opt.backward_step(&p_loss)?;
    }

    // パラメータの更新
    let input_x = x.expand(&[1, ndim])?;
    let nn_pred = proxy.forward(&input_x)?;
    let grads = nn_pred.backward()?;

    x_opt.step(&grads)?;

    // 経過時間の計測と結果の表示
    let elapsed = start.elapsed().as_micros();
    sum_time += elapsed as f64;

    if i % 100 == 0 {
        let f = objective(&x);
        dbg!(f);
        dbg!(sum_time / i as f64);
    }
}
最適化ループは大きく分けると以下の二つのステップに分けることが出来ます。
サロゲート関数の更新
パラメータの更新

 サロゲート関数の更新   // outerの正規分布に従ってパラメータをずらすための乱数を取得
    let samples = Tensor::randn(0.0, sigma, &[batchsize, ndim], &device)?;

    let x_batched = x.expand(&[batchsize, ndim])?;

    // サロゲート関数を学習するためのパラメータを作成
    let xs = Tensor::cat(&[&(&x_batched + &samples)?, &(&x_batched - &samples)?], 0)?;

    // サロゲート関数を学習するためのパラメータに目的関数を実行した値を作成
    let fs = (0..xs.shape().dims()[0])
        .map(|i| objective(&xs.get(i).unwrap()))
        .collect::<Vec<f32>>();
    let fs_tensor = Tensor::from_vec(fs.clone(), &[fs.len()], &device)?;

    // サロゲート関数の更新
    for _ in 0..3 {
        // サロゲート関数への入力を作成
        let xs_pert =
            (&xs - &Tensor::randn(0.0, 0.1 * sigma, &[batchsize * 2, ndim], &device)?)?;
        // サロゲート関数の出力を作成
        let nn_pred = proxy.forward(&xs_pert)?;
        // サロゲート関数と目的関数の出力のMSEを最小化するようにサロゲート関数のパラメータを更新する
        let p_loss = mse(&nn_pred.flatten_all().unwrap(), &fs_tensor)?;
        nn_opt.backward_step(&p_loss)?;
    }
ここでは、目的関数の結果を教師データとしてサロゲート関数のパラメータを更新します。

3回実行しているのは、こういう風にすると良いという風にZeroGradsのサプリメンタルに書いてあったので[3]そうしています。

図にすると以下のような感じになっています。

 パラメータの更新パラメータの更新は以下のコードで行われます：
// パラメータの更新
let input_x = x.expand(&[1, ndim])?;
let nn_pred = proxy.forward(&input_x)?;
let grads = nn_pred.backward()?;

x_opt.step(&grads)?;
この部分では、現在のパラメータ x をサロゲートモデルに入力し、その出力の勾配[4]を計算します。

その後、計算された勾配を使用してパラメータを更新します。
このプロセスにより、サロゲートモデルが近似した目的関数の勾配に基づいて、パラメータを最適な方向に更新することができます。
図にすると以下のような感じです。

 結果
 検証環境OS: MacOS
CPU: Apple M1 Max
メモリ: 64 GB
また、今回はサロゲート関数が小さいというのもありGPU(Metal)を利用するよりもCPU(Accelerate)を利用する方が早かったのでそちらを利用しています。

 実験結果 f(\bm{x}) = \sum_{i=1}^n{x_i} に対してZeroGradsで最適化を行った結果以下のようになりました。


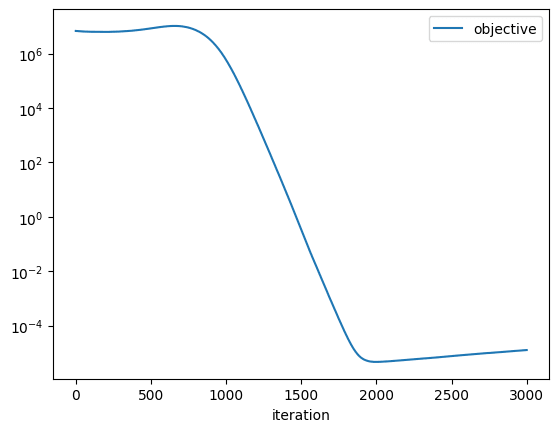
ZeroGradsで\bm{x}最適化した結果の目的関数のlogスケールでの推移
各ステップでの実行時間は以下のようになっています。
各ステップ大体数ミリ秒で動いていることがわかります。

 ベイズ最適化(Optuna)との比較
 追加実験ベイズ最適化と比較するために、
 f(\bm{x}) = \sum_{i=1}^n{x_i} に対して、ベイズ最適化の代表格である、Optuna(TPE)で最適化も行って結果を比較しました。(実行時間の関係でOptunaは1000回までの実行です)


OptunaとZeroGradsの目的関数値の比較
このケースにおいては、ZeroGradsの方が良く動作していることがわかります。
!今回の問題設定はZeroGradsに対して非常に有利な設定であるということに注意してください。
有利である理由は以下です。
入力が高次元であること
目的関数が凸であること
目的関数の実行が非常に高速であること


OptunaとZeroGradsのステップあたりの実行速度(ms)の推移の比較
optunaは実行回数に対して実行時間が増加しているにたいして、ZeroGradsでは実行時間が一定なことがわかります。
!実行速度に関しては今回の実験では(本実装の)ZeroGradsとOptunaでは実装言語に違いがあり単純に比較できないことに注意してください。

 共通点：ブラックボックス最適化ZeroGradsとOptunaは、どちらもブラックボックス最適化のツールとして機能します。つまり、最適化対象の関数の内部構造や勾配情報を必要とせず、関数の入出力のみを用いて最適化を行うことができます。この特性により、両者は幅広い問題に適用可能です。

 計算時間の特性の違い実験結果でもわかるとおり、OptunaとZeroGradsの違いの一つとして、反復回数に対する計算時間の伸び方にあります。
ベイズ最適化 (TPE アルゴリズム使用時):
i回目の実行速度はiによって増加します。計算量は O(dn \log n)

で表されます（dは次元数、nは反復回数）。
この特性により、Optunaの公式ドキュメントでは、100〜1000回の反復が推奨されています。これは計算時間と最適化の効果のバランスを考慮した推奨値です。
反復回数を増やすことは可能ですが、計算時間が急激に増加する可能性があります。
ZeroGrads:
i回目の計算時間はiに比例しません。つまり、反復回数が増えても各反復の計算時間は大きく増加しません。
これにより、より多くの反復を実行することが可能で、特に高次元の問題や複雑な最適化タスクに適しています。

 高次元パラメータ空間での性能入力パラメータが高次元の場合、ZeroGradsの方が優位性を持つ可能性があります：
ZeroGradsは、サロゲートモデルとしてニューラルネットワークを使用しており、高次元の関数扱いに適しています。
ベイズ最適化はパラメータの探索空間が次元が増えるにつれて爆発的に大きくなっていくため高次元の関数の扱いが苦手な可能性が高いです。

 目的関数の実行時間による影響目的関数の実行時間が短い場合、ZeroGradsの方が有利な場合があります：
Optunaは各反復で目的関数の評価を行うため、反復回数の増加に伴い総計算時間が直接的に増加します。
一方、ZeroGradsはサロゲートモデルを使用するため、目的関数の評価回数を抑えつつ、多数の反復を行うことができます。

 使用シナリオの考察Optunaが適している場合:
低〜中程度の次元のパラメータ空間
目的関数の実行に時間がかかる問題
ハイパーパラメータ調整など、比較的少ない反復回数で結果を得たい場合
ZeroGradsが適している場合:
高次元のパラメータ空間を持つ問題
目的関数の実行が比較的高速な問題
多数の反復を行うことで、より精密な最適化が求められる場合
ただし、ZeroGradsの利用用途に関しては他のメタヒューリスティクな最適化手法(山登り方、SA、GAなど)とかぶる部分があるためそこに対しても比較が必要です。ZeroGradsの実装[1:1]ではそこに関しても比較されています。

 最後に本記事では、ZeroGradsアルゴリズムのRust実装について詳しく解説し、高次元の最適化問題に対するその効果を検証しました。
ZeroGradsはまだ発表されて間もない手法ですが、ブラックボックス関数最適化に対して良いツールになる可能性を秘めていると思いました。

まだ、活用事例が出て来ていないですが、kaggleやAHCなどでトップ解法として取り上げられたりすると一気に有名になったりするのでそうならないかなとか思っています。
今回は実装や実験メインの記事になったので機会があれば論文の中に突っ込んだ記事も書いてみようかと思っています。

脚注
数学的な話と言うよりは、pytorchなどでbackward出来ない関数という程度の意味です ↩︎ ↩︎
このノートブックになります。(実行は自己責任でお願います) ↩︎
https://mfischer-ucl.github.io/assets/zerograds_supplemental.pdf ↩︎
サロゲート関数は目的関数(誤差関数)を直接推定する関数になっているので別途に誤差関数に入れること無く勾配をとって問題ありません。 ↩︎