Bloch球のよくある説明と謎
電子のスピンなどの二準位系
\ket{\psi} = a \ket{0} + b\ket{1}
=
\begin{bmatrix}
a\\
b
\end{bmatrix}
は量子情報処理ではqubit(量子ビット)と呼ばれます。
ここでa,bは 規格化条件|a|^2+|b|^2=1を満たす複素数です。
規格化条件を考慮すれば、一つのqubitの状態は適当な実数変数\theta,s,tを用いて、次のようにも書き表せます。
\ket{\psi} =
e^{is}\cos\frac{\theta}{2}\ket{0} + e^{it}\sin\frac{\theta}{2}\ket{1}
=e^{is}\left(\cos\frac{\theta}{2}\ket{0}
+e^{i(t-s)}\sin\frac{\theta}{2}\ket{1} \right)
量子状態全体にかかる大きさ1の係数e^{is}は量子状態に影響を与えないので、結局一つのqubitの任意の純粋状態は次のように掛けます。
\begin{align}
\therefore\ket{\psi} =
\cos\frac{\theta}{2}\ket{0}+e^{i \phi}\sin\frac{\theta}{2}\ket{1}
\end{align}
さて、よくある量子情報理論の教科書では、「任意の1qubitは二つの偏角(\theta,\phi)で表せるので、三次元座標の原点から単位球上の一点に伸びるベクトルで量子状態を指定することができます。この球をBloch球と言います」と説明されます。
この説明、なんか奇妙じゃないですか?
まず、三次元球上の一点を表すなら、三次元のベクトルで量子状態は表されるべきです。でも\ket{\phi}は二次元ベクトルです。ブロッホ球上のベクトルと\ket{\phi}はどのように対応しているのでしょうか?
そもそも角度はなぜ\thetaではなく、\frac{\theta}{2}で定義されるのでしょうか?
この記事では普段はあまり気にされないこの謎を解き、qubitの量子状態とBloch球がどのように対応するかを明らかにしたいと思います。
qubit stateとBloch球の対応
先ず、以下の数学的事実を確認します。
\begin{align}
u := \frac{b}{a} = e^{i\phi}\tan\frac{\theta}{2}
\end{align}
と1:1で対応する。
- 複素平面上の任意の点Aと複素平面zの原点を中心とする三次元単位球を考える(図1)。
球の北極((x,y,z)=(0,0,1))と点Aを結んだ線は単位球の球面とただ1点Pで交わる。図1にはPが南半球にある状況と、Pが北半球にある状況を図示した。点Aの座標を(v,w)と書いたとき、点Pの座標は、幾何学の計算より、
\begin{align}
x = \frac{2v}{1+v^2+w^2}=\frac{2 \mathrm{Re} (u)}{1+|u|^2} \\
y = \frac{2w}{1+v^2+w^2}=\frac{2 \mathrm{Im} (u)}{1+|u|^2} \\
z = \frac{1-v^2-w^2}{1+v^2+w^2}=\frac{1-|u|^2}{1+|u|^2}
\end{align}
で与えられる。
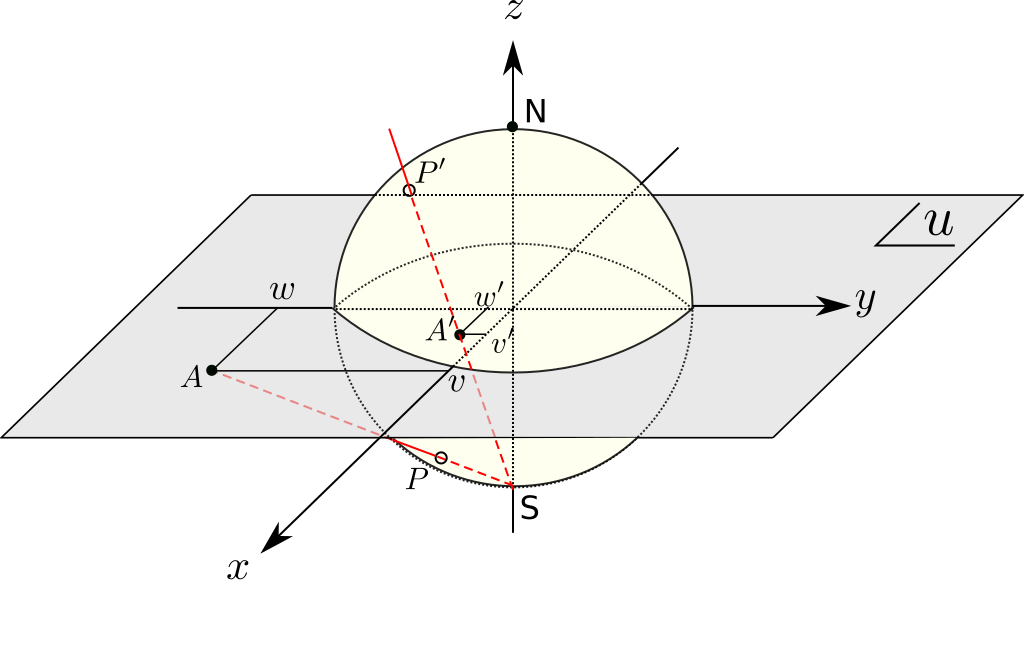
図1. 複素平面と三次元単位球
上記の事実を使うと、uの値を元に点Aを決めることができれば、\ket{\psi}を三次元単位球の球面上の点に対応させられそうです。実際にやってみます。uの実部、虚部をそれぞれv,wと定義します。
\begin{align}
u = \frac{b}{a} = e^{i\phi}\tan\frac{\theta}{2}= \cos\phi\tan\frac{\theta}{2}+i \sin\phi\tan\frac{\theta}{2} =: v + iw
\end{align}
式(3)- 式(5)に式(6)を代入すると
\begin{align}
x = \sin \theta \cos \phi, \quad y=\sin \theta \sin \phi, \quad z=\cos \theta
\end{align}
と求まります。これは三次元単位球の球面上の点の極座標表示そのものですね。そして量子状態では\theta/2で定義されていた角度はBloch球上では\thetaに相当することがはっきりしました。
実際に確かめてみると、\theta=0ではu=b/a=0; b=0より\ket{\phi}=\ket{0}, \theta=\piではu=b/a=\infty; a=0より\ket{\phi}=\ket{1}であり、確かにBloch球と一致します。
以上より、任意の2準位純粋量子状態\ket{\psi}は原点からBloch球上の点に伸びるベクトルと対応することが確認できました。
\ket{\psi}=a\ket{0}+b\ket{1}= \cos\frac{\theta}{2}\ket{0}+e^{i\phi}\sin\frac{\theta}{2}\ket{1}
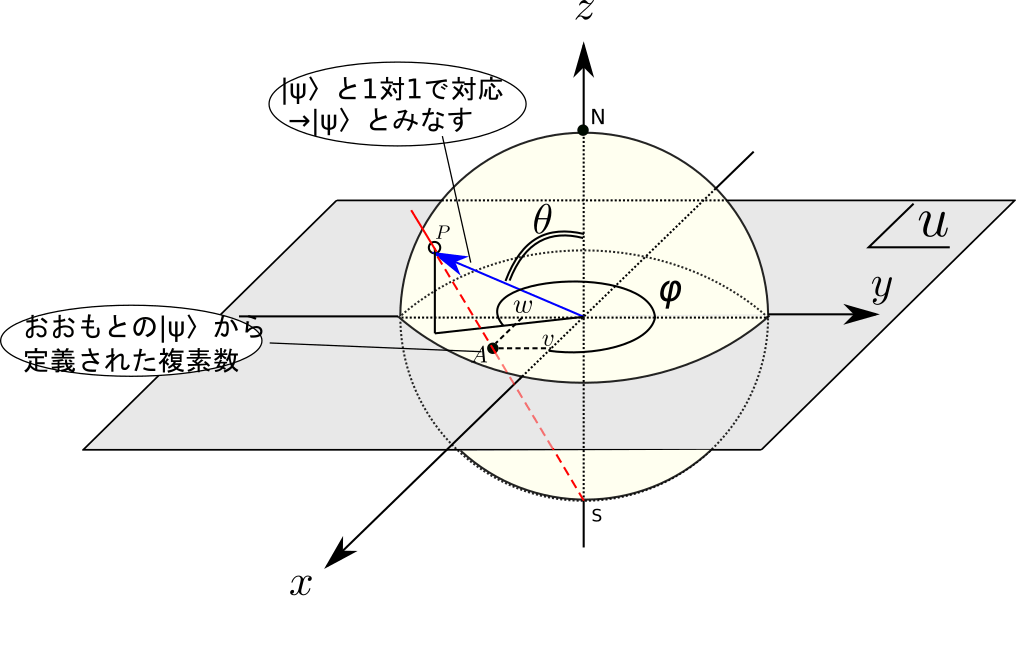
図2. Bloch球
任意1量子演算のBloch球上での見え方
1qubitの状態の変換はユニタリ変換Uで表されます。量子状態\ket{\psi}のユニタリ変換はBloch球上ではどのように表されるのか調べてみましょう。具体的なUの形として、天下り的ですが、以下の三つのユニタリ行列R_x,R_y,R_zの性質を調べます。
\begin{align}
R_x(\alpha):=&
\begin{bmatrix}
\cos \frac{\alpha}{2} && -i \sin \frac{\alpha}{2} \\
-i\sin \frac{\alpha}{2} &&\cos \frac{\alpha}{2}
\end{bmatrix}
=\exp\left(-i\frac{\alpha}{2}X \right) ,\quad
X :=
\begin{bmatrix}
0 && 1
\\1&&0
\end{bmatrix}
\\
R_y(\alpha):=&
\begin{bmatrix}
\cos \frac{\alpha}{2} && - \sin \frac{\alpha}{2} \\
\sin \frac{\alpha}{2} &&\cos \frac{\alpha}{2}
\end{bmatrix}
=\exp\left(-i\frac{\alpha}{2}Y \right) ,\quad
Y :=
\begin{bmatrix}
0 && -i
\\i&&0
\end{bmatrix}
\\
R_z(\alpha):=&
\begin{bmatrix}
e^{-i\frac{\alpha}{2}} && 0 \\
0 && e^{i\frac{\alpha}{2}}
\end{bmatrix}
=\exp\left(-i\frac{\alpha}{2}Z \right) ,\quad
Z :=
\begin{bmatrix}
1 && 0\\
0&&-1
\end{bmatrix}
\end{align}
行列X,Y,Zはパウリ行列です。。
R_x,R_y,R_z定義式の二つ目のイコールでは行列の指数表式の定義式
e^A := I + A + \frac{1}{2!}A^2 + \frac{1}{3!}A^3 + ...
を使用しています。パウリ行列は二乗するとIになるのでこの性質とオイラーの公式を使えば二つの目のイコールが示せますね。
R_z
まずはR_zが量子状態\ket{\psi}をどのように変化させるか見ましょう。
\ket{\psi},uそれぞれの変換後の状態は
\begin{align}
\ket{\psi'}=& R_z(\alpha) \ket{\psi} =
\begin{bmatrix}
e^{-i\frac{\alpha}{2}} && 0 \\ 0 && e^{i\frac{\alpha}{2}}
\end{bmatrix}
\begin{bmatrix}
\cos \frac{\theta}{2} \\ e^{i\phi} \sin \frac{\theta}{2}
\end{bmatrix}\\
= & e^{-i\frac{\alpha}{2}}
\begin{bmatrix}
\cos \frac{\theta}{2} \\ e^{i(\alpha+\phi)} \sin \frac{\theta}{2}
\end{bmatrix}
\sim
\begin{bmatrix}
\cos \frac{\theta}{2} \\ e^{i(\alpha+\phi)} \sin \frac{\theta}{2}
\end{bmatrix}\\
u' =& e^{i(\alpha+\phi)}\tan \frac{\theta}{2}
\end{align}
です。よってブロッホ球上での点P'は以下のように動きます。
\begin{align}
x' =& \frac{2 \mathrm{Re} (u')}{1+|u'|^2} = \frac{2 \cos (\alpha+\phi)\tan\frac{\theta}{2}}{1+\tan ^2 \frac{\theta}{2}} \\
= & \cos \alpha \cos \phi \sin \theta - \sin \alpha \sin \phi \sin \theta = x \cos \alpha - y \sin \alpha \\
y' =& \frac{2 \mathrm{Im} (u')}{1+|u'|^2} = \frac{2 \sin (\alpha+\phi)\tan\frac{\theta}{2}}{1+\tan ^2 \frac{\theta}{2}} \\
= & \sin \alpha \cos \phi \sin \theta + \cos \alpha \sin \phi \sin \theta = x \sin \alpha + y \cos \alpha \\
z' =& \frac{1-|u'|^2}{1+|u'|^2} = \frac{1-\tan^2 \frac{\theta}{2}}{1+\tan^2 \frac{\theta}{2}} \\
= & \cos \theta = z
\end{align}
行列で書けば
\begin{bmatrix}
x' \\ y' \\ z'
\end{bmatrix}
=
\begin{bmatrix}
\cos \alpha && -\sin\alpha && 0 \\ \sin \alpha && \cos\alpha && 0 \\ 0&& 0 && 1
\end{bmatrix}
\begin{bmatrix}
x \\ y \\ z
\end{bmatrix}
です。つまりR_zは三次元空間でのz軸周りに\alphaだけ点Pを回転させる演算を意味している事がわかります。
R_x
同様の計算をR_xでも行います。
\ket{\psi},uそれぞれの変換後の状態は
\begin{align}
\ket{\psi'} &= R_x(\alpha) \ket{\psi} =
\begin{bmatrix}
\cos \frac{\alpha}{2} && - i\sin \frac{\alpha}{2} \\
-i\sin \frac{\alpha}{2} &&\cos \frac{\alpha}{2}
\end{bmatrix}
\begin{bmatrix}
\cos \frac{\theta}{2} \\ e^{i\phi} \sin \frac{\theta}{2}
\end{bmatrix}\\
&=
\begin{bmatrix}
\cos \frac{\alpha}{2}\sin \frac{\theta}{2} -i e^{i\phi}\sin \frac{\alpha}{2}\sin \frac{\theta}{2} \\
-i \sin \frac{\alpha}{2}\cos \frac{\theta}{2} +e^{i\phi}\cos \frac{\alpha}{2}\sin \frac{\theta}{2}
\end{bmatrix}\\
u' &= \frac{-i \sin \frac{\alpha}{2}\cos \frac{\theta}{2} +e^{i\phi}\cos \frac{\alpha}{2}\sin \frac{\theta}{2} }{ \cos \frac{\alpha}{2}\sin \frac{\theta}{2} -i e^{i\phi}\sin \frac{\alpha}{2}\sin \frac{\theta}{2}}
\end{align}
より移動後のP'の座標と移動前のPの座標はがんばって計算すると
\therefore
\begin{bmatrix}
x' \\ y' \\ z'
\end{bmatrix}
=
\begin{bmatrix}
1 && 0 && 0 \\ 0 && \cos\alpha && -\sin \alpha \\
0&& \sin\alpha && \cos \alpha
\end{bmatrix}
\begin{bmatrix}
x \\ y \\ z
\end{bmatrix}
という関係であることがわかります。つまりR_xは三次元空間でのx軸周りに\alphaだけ点Pを回転させる演算を意味しています。
R_y
同様の計算をR_yでも行います。
\ket{\psi},uそれぞれの変換後の状態は
\begin{align}
\ket{\psi'} &= R_y(\alpha) \ket{\psi} =
\begin{bmatrix}
\cos \frac{\alpha}{2} && - \sin \frac{\alpha}{2} \\
\sin \frac{\alpha}{2} &&\cos \frac{\alpha}{2} )
\end{bmatrix}
\begin{bmatrix}
\cos \frac{\theta}{2} \\
e^{i\phi} \sin \frac{\theta}{2}
\end{bmatrix}\\
&=
\begin{bmatrix}
\cos \frac{\alpha}{2}\sin \frac{\theta}{2} -e^{i\phi}\sin \frac{\alpha}{2}\sin \frac{\theta}{2} \\
\sin \frac{\alpha}{2}\cos \frac{\theta}{2} +e^{i\phi}\cos \frac{\alpha}{2}\sin \frac{\theta}{2}
\end{bmatrix}\\
u' &= \frac{ \sin \frac{\alpha}{2}\cos \frac{\theta}{2} +e^{i\phi}\cos \frac{\alpha}{2}\sin \frac{\theta}{2} }{ \cos \frac{\alpha}{2}\sin \frac{\theta}{2} -e^{i\phi}\sin \frac{\alpha}{2}\sin \frac{\theta}{2}}
\end{align}
より移動後のP'の座標と移動前のPの座標はがんばって計算すると
\begin{bmatrix}
x'\\ y' \\ z'
\end{bmatrix}
=
\begin{bmatrix}
\cos\alpha && 0 && \sin\alpha \\ 0 && 1 && 0 \\ -\sin\alpha&& 0 && \cos \alpha
\end{bmatrix}
\begin{bmatrix}
x \\ y \\ z
\end{bmatrix}
という関係であることがわかります。つまりR_yは三次元空間でのy軸周りに\alphaだけ点Pを回転させる演算を意味しています。
任意演算
以上の通り、天下り的に定義した3つのユニタリ行列R_x,R_y,R_zはそれぞれブロッホ球上でのx,y,z軸周りの回転に対応している事がわかりました。
三次元単位球の球面上での任意の回転は数学的にx,y,z軸周りの3回転のうち2つの回転で表現できることが知られています。例えばn軸周りの3x3の三次元回転行列を\mathcal{R_n}で表した時、任意の(=任意のn軸周りの)回転は
\mathcal{R_n} = \mathcal{R}_z(\alpha) \mathcal{R}_y(\beta) \mathcal{R}_z(\gamma)
という風にy軸周りの回転とz軸周りの回転に分解できます。
この事実を考えれば、任意の状態ベクトルの変換もR_x,R_y,R_zのうち2つを選ぶことで分解できる事がわかるでしょう。試しにR_y,R_zで分解して表現してみると、
\begin{align}
U (\theta,\phi,\lambda)&= R_z (\phi)R_y (\theta) R_z (\lambda) \\
&=
\begin{bmatrix}
e^{-i\frac{\phi}{2}} && 0
\\ 0 && e^{i\frac{\phi}{2}}
\end{bmatrix}
\begin{bmatrix}
\cos \frac{\theta}{2} && - \sin \frac{\theta}{2}
\\ \sin \frac{\theta}{2} &&\cos \frac{\theta}{2}
\end{bmatrix}
\begin{bmatrix}
e^{-i\frac{\lambda}{2}} && 0 \\ 0 && e^{i\frac{\lambda}{2}}
\end{bmatrix}\\
&=
e^{-i \frac{\phi+\lambda}{2}}
\begin{bmatrix}
\cos \frac{\theta}{2} && - e^{i\lambda}\sin \frac{\theta}{2}
\\ e^{i\phi}\sin \frac{\theta}{2} && e^{i(\phi+\lambda)}\cos \frac{\theta}{2}
\end{bmatrix}
\end{align}
と計算でき、結局1 qubitの任意演算は
U (\theta,\phi,\lambda)=
\begin{bmatrix}
\cos \frac{\theta}{2} && - e^{i\lambda}\sin \frac{\theta}{2}\\
e^{i\phi}\sin \frac{\theta}{2} && e^{i(\phi+\lambda)}\cos \frac{\theta}{2}
\end{bmatrix}
とまとめることができます。この演算はUゲートと呼ばれており、Qiskitにも登録されています。
https://qiskit.org/documentation/stubs/qiskit.circuit.library.UGate.html
Reference


Discussion