🧮

標数2の体のためのx64用SIMD命令

2023/07/07に公開

aes

初めに

今回は標数2の体の実装に利用でいるx64用SIMD命令を紹介します。この記事は

暗号で使われる標数2の体
暗号で使われる標数2の体の実装
の続きです。AES専用命令AES-NIは今回ターゲットから外れるためまたの機会とします。

PCLMULQDQ

Packed Carry-Less MULtiplication Quadwordという命令です。"packed"は整数系SIMD, "carry-less multiplication"はcarryの無い乗算という意味です。SSE版だけでなくAVXやAVX-512版のvpclmulqdqもあります。
普通の整数乗算は計算途中で繰り上がりが発生します（cf. 多倍長整数の実装4（乗算の基礎））。
しかし、標数2の体では加法は排他的論理和、乗法は論理積なので繰り上がりがありません。そのため"carry-less"とついています。具体的には多項式の乗算に現れた式を計算します。
すなわち、 $a=\sum_{i=0}^{n-1} a_i X^i$ , $b=\sum_{i=0}^{n-1} b_i X^i$ に対して $c=ab$ としたとき

c_i = \begin{cases} \sum_{j=0}^i a_j b_{i-j} & (i=0, \dots, n-1),\\ \sum_{j=i-n+1}^{n-1} a_j b_{i-j} & (i=n, \dots, 2n-2). \end{cases}

命令の最後の"qdq"はqword（64ビット）の乗算でdouble qword（128ビット）の結果を得るという意味で、 $n=64$ 固定です。

前回主に8次拡大体の実装方法を紹介しましたが、 $𝔽_2$ の8次拡大体と128次拡大体で紹介したように、AES-GCMやXTS-AESでは128次拡大体が使われます。その乗算処理を高速化するために導入されました。
その詳細はIntel Carry-Less Multiplication Instruction and its Usage for Computing the GCM Modeにあるので、ここでは簡単に紹介します。

128次多項式の乗算

(v)pclmulqdqは正確には vpclmulqdq(z, x, y, imm) という4個の引数をとります。
x, yは128ビット単位のSIMDレジスタxL, yL, xH, yHと書くとそれぞれx, yの下位64ビット、上位64ビットを表すことにします。immの値に応じて{xH,xL}×{yH,yL}の4通り選択でき、名前のエリアスがつけられています。

imm	エリアス名	x	y
0x00	vpclmullqlqdq	xL	yL
0x10	vpclmulhqlqdq	xH	yL
0x01	vpclmullqhqdq	xL	yH
0x11	vpclmulhqhqdq	xH	yH

128次同士の多項式の乗算はこれらの64次多項式乗算を使って実現します。繰り上がりが無いので難しくはありません。
xL yL, xL yH, xH yL, xH yHの乗算を計算し、それぞれ重なっている部分で排他的論理和をとればよいです。

xy = ([xH yH] << 128) ^ ([xH yL] << 64) ^ ([xL yH] << 64) ^ [xL yL]

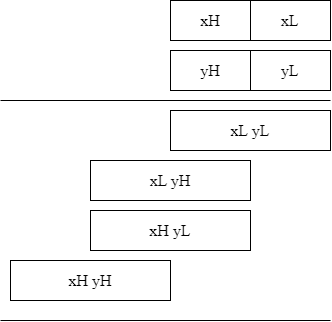
pclmulqdq
64ビット乗算を使った128ビット乗算

この後の $K=𝔽_{2^{128}}$ におけるmod演算は簡単なビットシフトと排他的論理和をとります。詳細は前述のIntelのPDFをご覧ください。

GFNI命令

8次拡大体 $K=𝔽_{2^8}$ について、乗算はそのものずばりのvgf2p8mulbという命令があります。"Galios Field of 2 to the Power 8"の略でしょうか。
cpuidでGFNIが有効だと使えます。AVX-512として使う場合にはGFNIとAVX512Fの両方が有効でないと使えないことに注意してください。
この命令はSIMDの8ビット要素ごとに $K$ での乗算をします。つまり暗号で使われる標数2の体の実装の計算をAVX-512なら512/8 = 64個同時にします。IceLakeによるとレイテンシ3のスループットが0.5~1と、単純な実装より1, 2桁速いです。
逆数を求める命令gf2p8affineinvqbもあります。やたら長い名前ですね。調べた限りではx64命令の中で一番長かったです。単に逆元(inverse)を求めるだけでなくAffine変換も入ってます。

gf2p8affineinvqb(z, x, y, imm8) # z ← inv(x) * y + im8

xの逆数inv(x)に行列yを掛けてimm8を足します。「行列を掛けて定数を足す」部分がAffine変換です。
より正確にはyは64ビット単位のSIMDで64ビットを8x8のビット行列Yとみなし、8ビット単位のxをサイズ8の行列とみなして「Yx+imm8」を計算するのです。計算における積や和は、やはり論理積や排他的論理和であることに注意してください。
単に逆数を求めたいならYは単位行列を設定し、imm8=0として呼び出せばよいです。
単位行列は64ビット整数で表すと0x0102040810204080です。

10000000 // 0x80
01000000 // 0x40
00100000 // 0x20
00010000 // 0x10
00001000 // 0x08
00000100 // 0x04
00000010 // 0x02
00000001 // 0x01

呼び出し例（あくまでサンプル）

  makeLabel('matrixI')
  dq_(0x0102040810204080)

  # 256/8=32個のbyte配列x[32]の逆元を求めてy[32]に保存する
  # gf256_inv_gfni(uint8_t y[32], const uint8_t x[32]);
  with FuncProc('gf256_inv_gfni'):
    with StackFrame(2, vNum=2, vType=T_YMM) as sf:
      py = sf.p[0]
      px = sf.p[1]
      vmovups(ymm0, ptr(px))
      vbroadcastsd(ymm1, ptr(rip+'matrixI'))
      # ymm0 * matrixI + 0
      vgf2p8affineinvqb(ymm0, ymm0, ymm1, 0)
      vmovups(ptr(py), ymm0)

逆数のAffine変換ではなくxのAffine変換のみを求める命令gf2p8affineqbもあります。

gf2p8affineqb(z, x, y, imm8) # z ← x * y + imm8

gf2p8affineqbを用いたビット反転(bit reverse)

高速Fourier変換FFTなどではある整数値のbit reverseが必要になることがあります。
bit reverseとはたとえば8ビット整数a=[a7:a6:a5:a4:a3:a2:a1:a0]ならbitRev(a)=[a0:a1:a2:a3:a4:a5:a6:a7]とすることです。
bitRevはシフトやorなどのビット演算の組み合わせ、あるいは8ビットテーブル引きをして16ビット整数や32ビット整数のbitRevを実現します。
ここではgf2p8affineqbを使ったやり方を紹介します。と言っても単純で、前節のAffine変換では単位行列を使った部分を

00000001 // 0x01
00000010 // 0x02
00000100 // 0x04
00001000 // 0x08
00010000 // 0x10
00100000 // 0x20
01000000 // 0x40
10000000 // 0x80

にするだけです。8ビット内でbitRevができれば後はbswapか、複数個同時にするならvpshufbやvpermbを使ってバイト単位の反転をすればよいです。

def gen_bitRev():
  with FuncProc('bitRev_gfni'):
    with StackFrame(1, vNum=2, vType=T_XMM) as sf:
      x = sf.p[0]
      bswap(x)
      vmovq(xmm0, x)
      mov(rax, 0x8040201008040201)
      vmovq(xmm1, rax)
      vgf2p8affineqb(xmm0, xmm0, xmm1, 0)
      vmovq(rax, xmm0)

他には8ビット単位でのAx+bの結果が(1<<L)以上かどうかの判定によってL個の(=0判定による)式のandといくつかの式のorのチェックもできますね(たとえば $x_0+x_2+x_3=0 \cap x_1 + x_2 + x_7=0 \cup x_3+x_4+1=0$ みたいな)。
具体的な応用例は今思いつきませんが、はまれば使える部分がありそうです。

まとめ

標数2の拡大体の演算を高速化するためのPCLMULQDQとGFNI命令を紹介しました。暗号用途に追加された命令群ではありますが、それ以外の使い道が無いか考えてみると面白いかもしれません。

GitHubで編集を提案