2次拡大体とlazyリダクション

初めに

前回、2次拡大体の基本ではKaratsuba法を用いた乗算の高速化手法を紹介しました。
今回はその昔(2010年)、High-Speed Software Implementation of the Optimal Ate Pairing over Barreto–Naehrig Curvesでペアリングの拡大体計算に適用した（lazy reductionと呼ばれる）手法を紹介します。

Montgomery乗算

一般に、大きな素数標数 $p$ の有限体の乗算はMontgomery乗算を使います。
$x, y \in 𝔽_p$ に対する mul(x, y) は $x$ と $y$ の通常の筆算の途中 $x y_i$ を計算したときに $pq$ （ $q=x y_i \bmod{2^{64}})$）を加算しながら計算しました。
これは通常の乗算を筆算の形で行うところの隙間にリダクション操作が挿入されています。

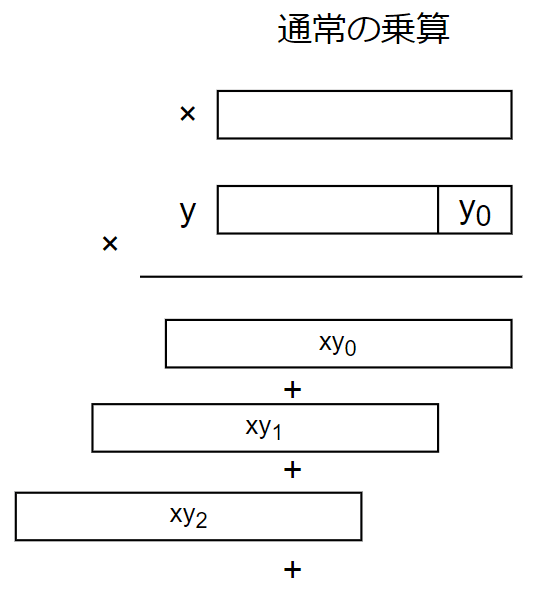
通常の乗算

Montgomery乗算

挿入された部分をよく観察すると、ipの計算はその一つ前の $x y_i$ の下位64bitで決まります。
そこで $xy$ の計算が完了してから、まとめてリダクションしても同じ結果を得ます。

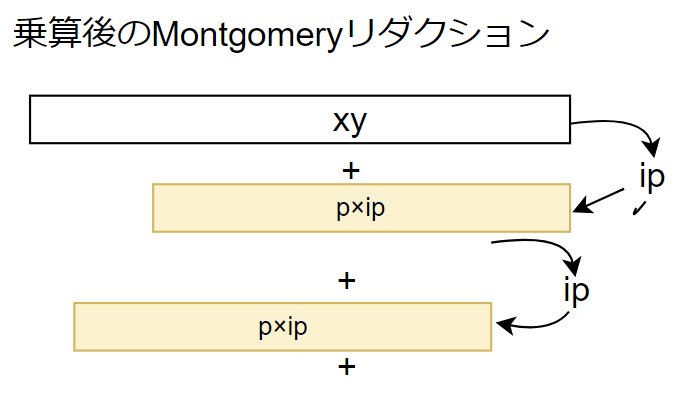
乗算後のリダクション

ここでは $x$, $y$ を $L$ ビット整数とし,

• $x y$ をリダクションなしに普通に乗算して $2L$ ビット整数を得る関数をmulPre
• $2L$ ビット整数をリダクションして $L$ ビット整数にする操作をred
  と呼ぶことにします。

$$\text{mul}(x, y) = \text{red}(\text{mulPre}(x, y))$$

lazyリダクションのアイデア

前回の2次拡大体の乗算は $f=a+bi$, $g=c+di$ に対して

$$(a+bi)(c+di)=(ac-bd)+(ad+bc)i = (ac-bd)+((a+b)(c+d)-ac-bd)i$$

と3回のMontgomery乗算でできることを示しました。この処理をより高速化します。
コアアイデアを紹介しましょう。以下mul(x, y)を $xy$ と略記します。

$x:=ac$, $y:=bd$, $z:=(a+b)(c+d)$ とおきます。
$xy=\text{red}(\text{mulPre}(x,y))$ なので $X:=\text{mulPre}(a, c)$, $Y:=\text{mulPre}(b, d)$, $Z=\text{mulPre}(a+b,c+d)$ とおきましょう。
$X$, $Y$, $Z$ はリダクション前の積の値なので $x=\text{red}(X)$, $y=\text{red}(Y)$, $z=\text{red}(Z)$ です。
そこでもし

• $\text{red}(X-Y)=ac-bd$
• $\text{red}(Z-X-Y)=(a+b)(c+d)-ac-bd=ad+bc$

となるなら、リダクションの回数を3回から2回に減らせます。

Xeon w9-3495Xでベンチマークをしたところ、$L=384$ のときmulPre, red, mulはそれぞれ約20clk, 30clk, 50clkでした。
つまり最初乗算mul 3回(20+30)x3=150clkだったのが、mulPre 3回とred 2回の20x3+30x2=120clkになります（ここでは加算回数の増加は無視）。

ここで高が30clkという勿れ。mul演算としては20%強の速度向上だし, mulはペアリング演算の殆どを占めるので全体の性能向上に直結します。こういうのを積み重ねないと世界最速にはならないです。

それはさておき、都度乗算 mul=mulPre+red をするのではなく、必要になる最後までリダクションを遅らせて、その回数を減らすテクニックなのでlazyリダクションといいます。

lazyリダクションの詳細

前節のアイデアを精密化しましょう。

まずMontgomery乗算の正当性で登場する入力値 $t$ が $t \le 2p-1$ であるという条件は、 redに対しては $L$ ビット左シフトされて $t <(2p-1)\times 2^L$ となります（条件C）。
素数 $p$ がfullでない ($p < 2^{L-1}$) とします。この条件はBLS12-381などのペアリング曲線パラメータで成立しています。$M:=2^L$ としましょう。
$a, b, c, d < p$ なので$a + b, c+d < 2p < 2^L=M$. $X=\text{mulPre}(a,c)$, $Y=\text{mulPre}(b,d)$ について$X, Y < p^2 < M/4$.

リダクションは $p$ で割った余りに関する操作なので条件Cを満たす限り $p$ の倍数を足しても結果は変わりません。
$X - Y$ はマイナスになる可能性があるため処理が煩雑になりますが、$X + (p M - Y) < M/2$ なので繰り上がりも繰り下がりも発生しません。
よって $\text{red}(X-Y)=\text{red}(X+p \cdot 2^L - Y)$ です。
同様に $Z - X - Y$ は常に0以上で $2p^2 < M/2$ より小さいです。したがって正しく計算できます。

なお、 $2L$ ビット長となっている $X$, $Y$ などの加減算は $L$ ビット長の2倍のコストがかかりますがモジュロ処理が無いのに対し、 $𝔽_p$ の加減算はモジュロ処理が入っているのでそれを考慮するとほぼ同じコストです。

リダクションの高速化

アセンブリ言語レベルで実装するときの細かなテクニックを一つ紹介します。
「mulとmulPre+redは同じ」と言いましたが、実装レベルでは異なります。
なぜなら、mulPreの結果は64ビットレジスタを12個必要(64x12=768)なので、x64では汎用レジスタが足りません。必然的に一度メモリに退避する必要があり、その分遅くなります（mulはx64でもメモリ退避せずに計算可能）。
それだけでなく、ナイーブに実装するとredは加算回数が増えてしまいます。「乗算後のリダクション」の図を見ると分かりますが、 $xy$ という768ビットの整数に $p \times \text{ip}$ を足すとき繰り上がりが伝播する可能性があるため最上位まで加算が必要です。

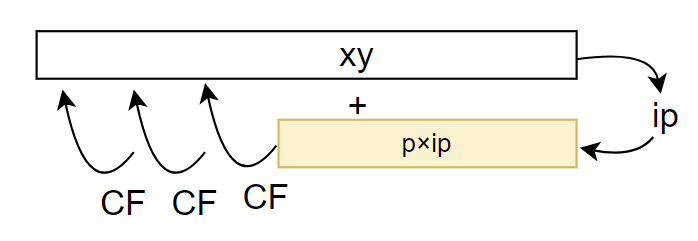
繰り上がりの連鎖

これを改善するために、 $p \times \text{ip}$ を加算したときに最初に発生するCFを一度レジスタに保存し、次の $p \times \text{ip}$ に加算してからそれを $xy$ に足すように変更します。

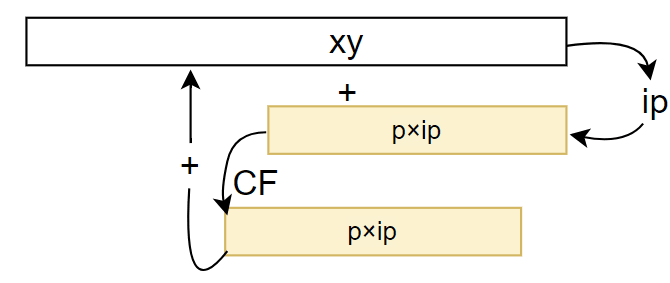
繰り上がりの連鎖が無い

$p$ が $L$ ビットで $B=64$ としたとき $p \times \text{ip}$ の最大値は $(2^L-1)(2^B-1)$ です。
このとき前回から繰り上がった1ビットのCFを $L$ ビットシフトして加算すると、

$$(2^L-1)(2^B-1) + 2^L = 2^{L+B}-(2^B-1) < 2^{L+B}.$$

つまり、新たな繰り上がりが発生しません。そのため $p \times \text{ip}$ を加算するのと同じコストで $xy$ に加算できます。
$L=384$ のとき元の方法だと繰り上がりのための加算は $6+5+\dots+1=21$ 回に対して、後者の方法は $11$ 回と約半分です。
このようにしてリダクションを高速化します。