🧮

楕円曲線暗号のための数学7（マルチスカラー倍算概要）

2024/08/02に公開

zksnark

初めに

ここでは楕円曲線の複数の点のスカラー倍算の和を高速に求める方法を紹介します。
この処理はゼロ知識証明zkSNARKなどで頻繁に利用されます。

記号の準備

$P_1, \dots, P_n$ を楕円曲線の点、 $x_1, \dots, x_n$ を有限体の点としたとき、 $Q=x_1 P_1 + \dots + x_n P_n$ を求めます。 $n$ は数千から数万の規模を想定しています。
マルチスカラー倍算、英語ではmsm (multi-scalar multiplication) と呼ばれることが多いのですが、それぞれの点 $P_i$ を $x_i$ 倍（スカラー倍）するだけでなく、最後に和を求めるまでを含めた処理なのであまりよい命名には思えません。

既存手法の問題点

GLV法の中で紹介したマルチスカラー倍算は $n=2$ のときの手法でした。
単独のスカラー倍算では、出力の $Q$ を2倍する操作dblを繰り返しながら、ビットが立っているときだけ加算addしました。
$n=2$ では出力の $Q$ のdbl操作をまとめることで効率化しました。
この方法は $n$ が大きくなっても適用できますが、dblの操作（1回だけ）に比べてaddの比率が大きくなる（ $n$ に比例）ので、うまみは減ります。
逆に、addに必要なルックアップテーブルは $n$ に比例して準備する必要があります。昔実験したとき、順番にスカラー倍を求めて足すのに比べて、ランダムアクセスが増える分、 $n$ が100~200 ぐらいで逆に遅くなりました。そのため、大きな $n$ については別の手法が望まれます。

$x_i$ が小さく $n$ が大きいときの考察

$x_i$ が数ビット（たとえば2ビット）しかなく、 $n$ が大きいときを考えてみましょう。
2ビットしかない場合、 $x_i$ のパターンは $0, 1, 2, 3$ しかありません。したがって、 $P_i$ のうちで、 $0$ 倍するもの、 $1$ 倍するもの……とグループに分けて、

\begin{align*} Q&=&0(P_{i_{0, 1}} + \dots + P_{i_{0, n_0}})\\ &+&1(P_{i_{1, 1}} + \dots + P_{i_{1, n_1}})\\ &+&2(P_{i_{2, 1}} + \dots + P_{i_{2, n_2}})\\ &+&3(P_{i_{3, 1}} + \dots + P_{i_{3, n_3}}). \end{align*}

と表現できます。コードとしては $x_i$ が $w$ ビットのとき、予め $2^w$ 個のテーブル $T$ を用意して、同じ倍数になるものを加算してまとめます。

T = [0]*n
for i in range(n):
  if x[i]:
    T[x[i]] += P[i]

とすれば、 $T[i]$ ( $i=1, 2, \dots, 2^w-1$ ) に $P_i$ の和が入ります。そのあと $Q=T[1] + 2 T[2] + \dots + (2^w-1)T[2^w-1]$ を求めます。この計算方法については次節で改めて紹介します。

Q=T[0] + 2T[1] + ... m T[m-1] の計算方法

ここでも、T[i] をそれぞれ $i$ 倍してから加算するのではなく、よりよい方法を考えましょう。
たとえば $m=8$ で後半を見ると、6 T[5] + 7 T[6] + 8 T[7] という形が現れます。これは 6 (T[5] + T[6] + T[7]) + T[6] + 2 T[7] とする方が効率がよいでしょう。
より一般的には後ろからの部分和 $R=\dots + T[m-1]$ を更新しながら $Q$ に加算するのがよさそうです。
図で表すと、 $T[0] + 2T[1] + \dots$ と上から順に加算するのではなく、縦に右から加算します。

三角和

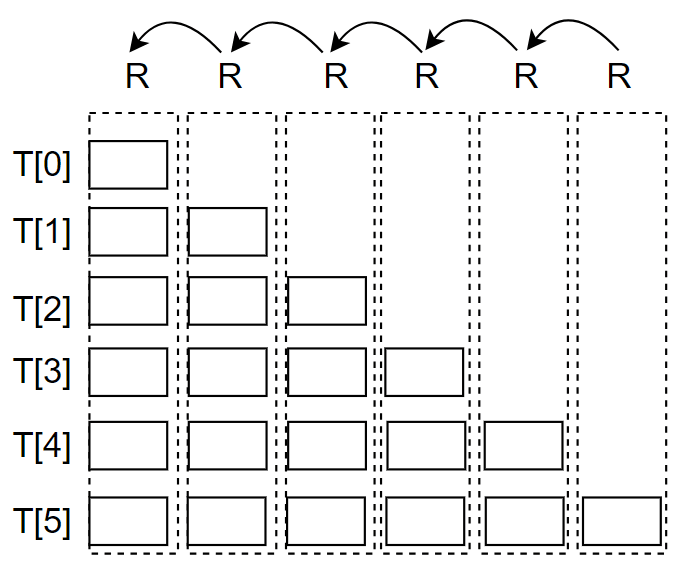
Pythonで記述すると次のようになります。

def f(T):
  Q = 0
  R = 0
  for i in range(m-1,-1,-1):
    R += T[i]
    Q += R
  return Q

ループの中身を追いかけると、

i	R	Q
m-1	T[m-1]	T[m-1]
m-2	T[m-1] + T[m-2]	2T[m-1]+T[m-2]
m-3	T[m-1] + T[m-2] + T[m-3]	3T[m-1] + 2T[m-2] + T[m-3]
...	...	...
0	T[m-1] + ... + T[0]	mT[m-1] + ... + T[0]

と欲しい結果が得られています。

全体のアルゴリズム

今までの考察をまとめると次の方法で計算します。

入力 : 楕円曲線の点 $P_1, \dots, P_n$ と有限体の点 $x_1, \dots, x_n$ .
出力 : $Q=x_1 P_1 + \dots + x_n P_n$ .

GLV法の自己準同型写像を用いて $x_i$ のビット数を半分にして $n$ を2倍にする。
改めてそれらを $P_1, \dots, P_n$ , $x_1, \dots, x_n$ とする。 $Q=0$ とする。
$x_i$ を $w$ ビットずつ区切り、上位部分を切り出して、今回紹介した方法で和を求める。
ステップ3で求めた和を $w$ 回dblしてから $Q$ に加算する。

ステップ3, 4を $w$ ビットずつ区切った個数分繰り返す。
より詳細なパラメータの決め方については次回考察します。

GitHubで編集を提案