楕円曲線暗号の安全性 DLPとCDHとDDH

初めに

TLSで利用される鍵共有ECDHや、楕円曲線を使ったlifted ElGamal暗号の安全性の根拠について解説します。
離散対数問題DLPが困難であるという仮定だけでは不十分なことを理解しましょう。

ECDH鍵共有の復習

$P$を楕円曲線の点、$G$を$P$を生成元とする位数$r$の加法巡回群とします。$G=\Set{0, P, 2P, \dots, (r-1)P}.$
$0$以上$r$未満の整数の集合を$[0, r)$と書く。

アリスとボブによる鍵共有

• アリスは乱数$a ← [0, r)$をとり、$aP$をボブに渡します。
• ボブは乱数$b ← [0, r)$をとり、$bP$をアリスに渡します。
• アリスは$a(bP)=abP$を、ボブは$b(aP)=abP$を計算して$abP$を共有します。

ECDH鍵共有

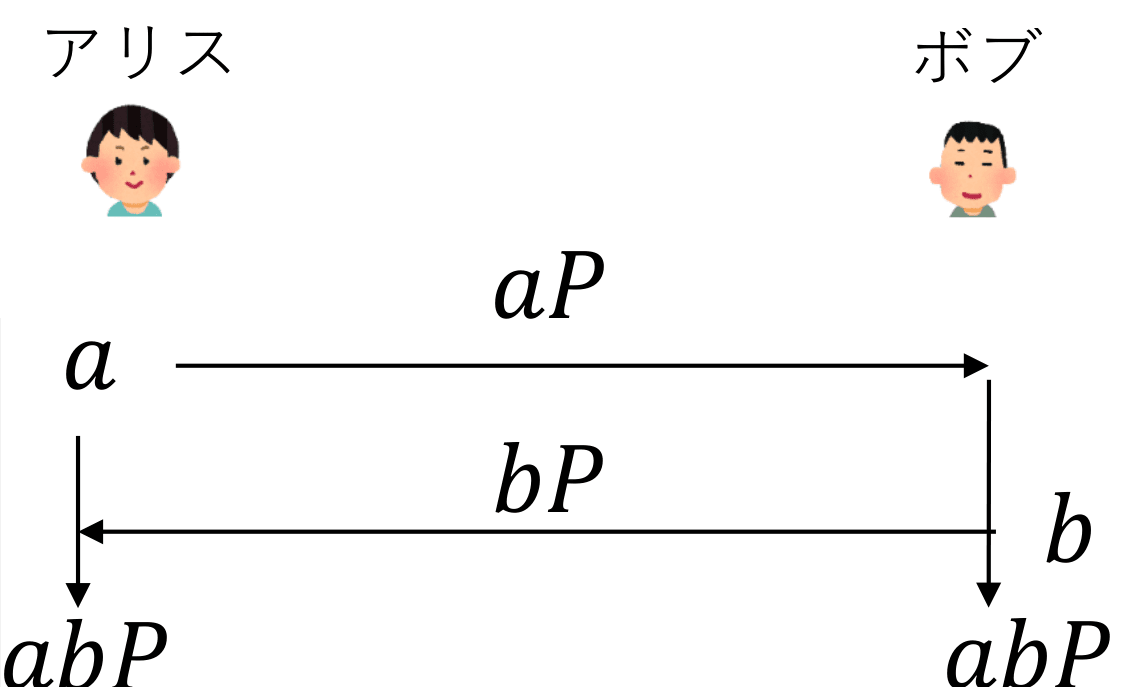
DLPが困難

離散対数問題DLP(discrete logarithm problem)とは$aP$と$P$が与えられたときに$a$を求める問題でした。
アリスとボブのやりとりを盗聴している人は$aP$と$bP$を入手できます。$P$は公開情報なのでDLPが解けると$a$や$b$が分かり、$abP$を計算できます。
これでは安全な通信とはいえません。そこで「DLPが困難な群$G$を使う」がDH鍵共有の必要条件です。

DLP困難

CDH仮定

公開情報$P$と盗聴者が入手した$aP$と$bP$からDLPを解かなくても直接$abP$を計算できてしまう可能性があります。
「$P$と$aP$と$bP$から$abP$を求める問題」をDH問題、より正確には計算DH、CDH(computational DH)問題といいます。
DH鍵共有はCDH問題が困難（CDH仮定が成り立つという）なら安全です。と言っても、これはほぼトートロジーです。

CDH仮定

なんだか頼りないなと思われたかもしれません。しかし、ここ数十年、CDH仮定は破られていません。明らかにDLPを解くよりはCDH問題を解く方が易しいですが、CDH問題が真に易しいかは未解決です（CDH問題が解けるならDLPも解けるか不明）。

RSA暗号の場合は

ちなみにこれはRSA暗号も似たようなものです。よく言われる「$N=pq$の素因数分解が解ければRSA暗号は破れる」は真ですが、素因数分解をしなくてもRSA暗号を破る方法があるかもしれません。
RSA暗号の安全性証明で使われるRSA仮定とはRSAの基礎の記号を使うと「$c$が与えられたときに$c=Enc(m)$となる$m$を求めよ」という問題が困難である、という仮定です。
RSA仮定を破れば素因数分解ができるのかは不明です。そのため「素因数分解が困難ならRSA暗号は安全」とは言えず、「RSA仮定が成り立つならRSA暗号は安全」としか言えません。こちらも殆どトートロジーですね。

(lifted) ElGamal暗号の安全性

さて(lifted) ElGamal暗号（以降liftedは面倒なので省略）の安全性の根拠を考えましょう。
鍵生成のときに秘密鍵$s ← [0, r)$を選んで、公開鍵$Q:=sP$を計算します。$Q$から$s$が求まってはいけないのでもちろんDLPが困難でなければなりません。

$m \in [0, r)$の暗号文は$c:=Enc(m;t)=(mP+tQ,tP)$でした（$t$は乱数）。

暗号化する側の不利な状況想定し、$m$は0か1のどちらかであると攻撃者が分かっているとします。$m$が、なんらかのyes/noで答える問題の答えだと十分ありえます。
攻撃者の立場になってみましょう。攻撃者は$P$と$Q$と$c$を入手しているので、そこからなんとか$m$の情報をゲットしたいです。

$m$は0か1のどちらかなので暗号文$c=(S,T)$は$Enc(0)=(tQ,tP)$か$Enc(1)=(P+tQ,tP)$のどちらかの形です。
$(Q,P)$は分かっているので$(S,T)$がそれを何倍かした$(tQ,tP)$だと判定できれば0の暗号文だとわかります。そのとき$t$は分からないままでも構いません。

ベクトルのスカラー倍

イメージとしては$(Q, P)$というベクトルの線上に暗号文$c=(S,T)$が乗っているかどうかを判定します。

DDH仮定

前節の考察をもう少し進めます。与えられた$T$が$P$の$t$倍としましょう。$T=tP$。ここでその$t$を知らなくても$S=tQ$であるかどうか分かればよいことになります。
$Q=sP$なので、$P$, $sP$, $tP$と$S$が与えられたときに$S=stP$か否か判定せよという問題です。$s→a$, $t→b$と置き換えると

$(P, aP, bP)$と$S$が与えられたときに$S = abP$か否かを判定せよ。

この問題を判定DH問題DDH(Decisional DH)といいます。CDH問題は$abP$を求める問題でしたが、DDH問題はそれが求まらなくても良い、ただ与えられた$S$に一致するかどうかだけ知りたい（=判定したい）という気持ちです。
もちろんCDH問題が解ければDDH問題は解けます。DDH問題が困難であるという仮定をDDH仮定といいます。今のところ、DDH仮定もCDH仮定と同じぐらい難しいと信じられています。

DDH仮定の元で、暗号文$c$が0か1のどちらかであるという情報をもらっても当てられないということが示されます。したがってElGamal暗号はそれぐらい安全であると言えます。

まとめ

DLPが困難、CDH仮定、DDH仮定という3種類の仮定を紹介しました。後者ほど仮定の条件が強く（より根拠が薄弱に）なります。
ECDH鍵共有はCDH仮定、ElGamal暗号はDDH仮定の元で安全です。