楕円曲線暗号のための数学2（バイナリ法によるスカラー倍算）

初めに

前回、楕円曲線暗号に必要な楕円曲線の点の加算を高速化するために射影座標を導入しました。
今回は楕円曲線の点の整数倍を計算する方法を紹介します。

スカラー倍算の定義

楕円曲線の点 $P$ をとり、 $n$ 個の和 $P+P\cdots + P$ を $nP$ と書きます。
楕円曲線の点の集合は加法群で、結合則が成り立つのでこの表記が使えます。
$n$ が負のときは $-((-n)P)$ とすることで、一般に点 $P$ の整数 $n$ 倍 $nP$ を計算できます。
この操作をスカラー倍算と呼びます。
ECDH鍵共有や楕円ElGamal暗号などで必須の演算です。

バイナリ法

以降、プログラムの中では楕円曲線の点のクラスを Ec, 点 $P$, $Q$ の和を add($P$, $Q$), 点 $P$ の2倍を dbl($P$) と書くことにします。
単に $n$ 個足せばよいのだから（以下簡単にするため $n > 0$ とします）、

def mul(P : Ec, n : int):
  Q = Ec()
  for i in range(n):
    Q = add(Q, P)
  return Q

とすれば一応求まります。しかし、このやり方は $n$ の大きさに比例して時間がかかります。
$n$ が256ビット整数ぐらいの大きさなら一生かかっても（宇宙の寿命がつきても）終わりません。

そこで、スカラー倍算を高速に計算する方法がいろいろ提案されています。まず一番基本的なバイナリ法を紹介します。
$n$ を1以上の整数として2進数展開します。

$$n=[n_{L-1}:n_{L-2}:\cdots:n_0]=\sum_{i=0}^{L-1} n_i 2^i.$$

ここで $n_i\in \Set{0,1}$ で $n_{L-1}=1$ とします。
$T:=P$ に対して $T:=\text{dbl}(T)=2P$, $T:=\text{dbl}(T)=2^2P$, $T:=\text{dbl}(T)=2^3 P$ と順次計算して $2^{L-1} P$ まで求めます。
そのとき 出力変数 $Q$ の初期値を 0 として $n$ の下位ビットから $n_i=1$ となるときの $T=2^i P$ を足していけば最終的に $nP$ が求まります。

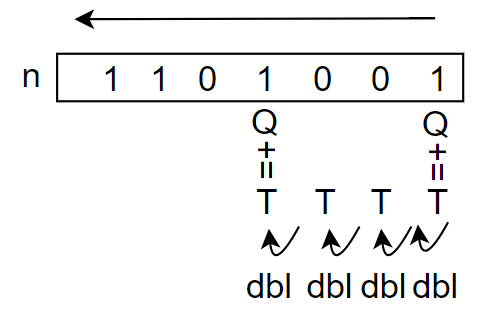
右から左へのバイナリ法

def mul1(P : Ec, n : int):
  bs = bin(n)[2:] # n を2進数展開して最初の `0b` を取り除いた文字列
  Q = Ec() # zero
  T = P
  for b in reversed(bs): # 下位ビットから順次計算
    if b == '1':
      Q = add(Q, T)
    T = dbl(T)
  return Q

このやり方は計算途中で $Q$ と $T$ の2個の変数を更新します。
逆に、$n$ の上位ビットから、出力変数 $Q$ を2倍しながら $n_i=1$ となるときに $P$ を足していけば更新変数は $Q$ だけにできます。

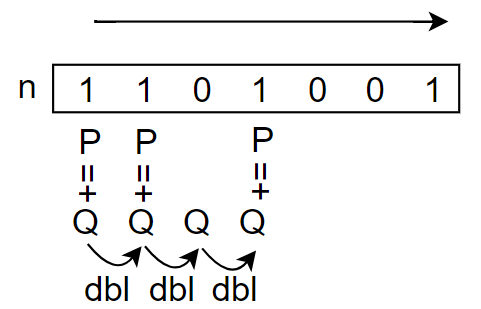
左から右へのバイナリ法

def mul2(P : Ec, n : int):
  bs = bin(n)[2:]
  Q = Ec() # zero
  for b in bs: # 上位ビットから順次計算
    Q = dbl(Q)
    if b == '1':
      Q = add(Q, P)
  return Q

バイナリ法の計算コスト

バイナリ法の演算コストを評価しましょう。add, dbl演算のコストをそれぞれ $A$, $D$ とします。
$n$ が $L$ ビットのとき、dblは $L$ 回するのでそのコストは $D A$ です。
addlは $n_i$ が1のときだけ必要です。一般に暗号で使われる $n$ は乱数なので $n_i$ は0と1が半分ずつと仮定します。
すると平均的に $L/2$ 回addするのでコストは $(L/2)A$ となり、合計 $DA + (L/2)A=L(D+A/2)=\log_2(n)(D+A/2)$ となります。
これはどちらのバイナリ法でも同じですね。