歩留まりに有意差があるか確かめる、あるいはベルヌーイ試行の成功率の信頼区間

TL;DR

• 歩留まりの数値(成功数/サンプル数)だけを比較しても、どちらが良いかはわからない
• だが、サンプル数と成功数から「成功確率はほぼ確実にpからqの間である」という範囲(信頼区間)を求めることができる
• 信頼区間を用いることで、自信を持って比較ができる
• 技術職のみならず、営業職や経営者にも役に立つ

イントロダクション

成功数xと試行回数Nがわかっている時、本当の成功率はわからないが、Nが十分に大きければ「成功率はx/Nに近い」と言える。しかし、特にNが小さい場合、「成功率はこの範囲にあるのではないか」という当たりをつけたいことがある。こういった場面で役立つのが信頼区間である。

信頼区間とは、かいつまんで説明するとこうだ。

例えば、サイコロを投げ、1が出たら成功、それ以外は失敗とする。この時の成功率の信頼区間を、成功した回数と試行回数を元に計算できる。
「70回中7回成功したので信頼区間は[5%, 19%]」
「10回中5回成功したので信頼区間は[24%, 76%]」
「90回中9回成功したので信頼区間は[5%, 18%]」
「20回中6回成功したので信頼区間は[15%, 52%]」
「100回中16回成功したので信頼区間は[10%, 24%]」
「20回中5回成功したので信頼区間は[11%, 47%]」
こうして信頼区間の算出を繰り返していくと、算出した信頼区間が真の確率(この場合16.666...%)を含んでいる割合(本稿では便宜上被覆率と呼ぶ)は一定の高い値(95%など)に漸近する。この値を信頼係数と呼ぶ。
すなわち、信頼区間は真の値を含んでいる可能性が高い^[1]。

具体的な計算方法

一定確率で「成功」「失敗」のどちらかになるような試行をベルヌーイ試行と呼ぶ。ベルヌーイ試行における成功率の信頼区間を求める手法はいくつか存在する。
https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval

Wald interval: 正規分布における信頼区間

$$p~~\approx ~~{\hat {p}}\pm {\frac {\;z_{\alpha }\ }{\ {\sqrt {n\;}}\ }}\ {\sqrt {{\hat {p}}\ \left(1-{\hat {p}}\right)\ }}$$

• $\hat{p}$: 歩留まり
• $n$: サンプルサイズ
• $z_\alpha$: zスコア (95%の場合1.96)

平均値と分散を用いる信頼区間の算出の定番の手法だが、$\hat{p}$が0や1に近いときに$\lbrack0,1\rbrack$を飛び出してしまったり、例えば10回中10回成功すると信頼区間の幅が0になってしまうなどの致命的な難点があり、実用的ではない。特に試行回数が少ない場合は使ってはいけないと言い切って良いだろう。

Wilson score interval

$$p~~\approx~~{\frac {1}{~1+\frac{z_{\alpha }^{2}}{n}~}}{\Bigg (}\ {\hat {p}}+{\frac {\;z_{\alpha }^{2}\ }{2\ n}}~~\pm ~~{\frac {\!\ z_{\alpha }\!\ }{\!\ 2\ n\!\ }}\ {\sqrt {\ 4\ n\ {\hat {p}}\ (1-{\hat {p}})+\ z_{\alpha }^{2}~}}~{\Biggr )}$$

Wald intervalの改良版で、上記二つの欠点が解消されており、サンプルサイズが小さくても使用できる。

イェーツの連続性補正 (a.k.a. continuity correction)を適用した変種として以下の式も使える。

$$w^- = \max \left\{0,~~\frac{2n\hat{p} + z_\alpha^2 - \left(z_\alpha\sqrt{ z_\alpha^2 - \frac{1}{ n } + 4n\hat{p}\left(1 - \hat{p}\right) + \left( 4\hat{p} - 2 \right) ~}+1\right)}{2 \left( n + z_\alpha^2 \right)}\right\}$$

$$w^+ = \min \left\{1,~~\frac{2n\hat{p} + z_\alpha^2 + \left(z_\alpha\sqrt{ z_\alpha^2 - \frac{1}{ n } + 4n\hat{p}\left(1 - \hat{p}\right) - \left( 4\hat{p} - 2 \right) ~}+1\right)}{2 \left( n + z_\alpha^2 \right)}\right\}$$

簡易計算式

Wilson score interval (z=1.96)に基づく計算式。SQLなどに組み込む際におすすめ。

• upper(x, N) = (x + 1.92 + 1.96 * sqrt(x * (N - x) / N + 0.96)) / (N + 3.84)
• lower(x, N) = (x + 1.92 - 1.96 * sqrt(x * (N - x) / N + 0.96)) / (N + 3.84)

Clopper–Pearson interval

初等的な数式では計算できないが、算出された信頼区間の被覆率が確実に信頼水準を上回るという特徴を持つ。理論的には最も素直な方法。

$$\lbrack{\ B^{-1}\!\left({\tfrac {\!\ \alpha \!\ }{2}}\ ;\ s\ ,\ n-s+1\right), B^{-1}\!\left(\ 1-{\tfrac {\!\ \alpha \!\ }{2}}\ ;\ s+1\ ,\ n-s\ \right)\ }\rbrack$$

ただし、$s$は成功数で、$B^{-1}(p; v, w)$はshape parameterをv, wとするベータ分布のp分位数。

Agresti–Coull interval

成功数と総数を補正("add two successes and two failures")してからWald intervalを算出する方法。比較的新しい^[2] 方法で、計算が容易なのが特長。

$$\tilde {p}={\frac {s+{\tfrac {\ z_{\alpha }^{2}}{2}}}{\!\ {n + z_\alpha^2}\!\ }}$$

$$p~~\approx ~~{\tilde {p}}~\pm ~z_{\alpha }\ {\sqrt {{\frac {\!\ {\tilde {p}\left(\!\ 1-{\tilde {p}}\!\ \right)}\!\ }{n + z_\alpha^2}}}}$$

性能の評価

それぞれの公式について、被覆率をモンテカルロ法を用いて評価する。
具体的には、あらかじめ決めた真の確率に従ってサンプリングを行い、そこから算出した信頼区間の被覆率^[3]を計算する。
この割合が信頼係数を上回っていれば、信頼区間の要件をよく満たしている。

詳細な条件は以下の通りである。

• 真の確率: 0%から100%まで1%刻み
• 信頼区間を算出するセッション数: 10000回
• 試行回数: 10から100までの10刻みの一様乱数
• 成功回数のサンプリング: 二項分布に従う疑似乱数生成機を使用
• z値: 1.96 (信頼水準95%相当)

以下のグラフは、縦軸は被覆率、横軸は真の確率を表している。

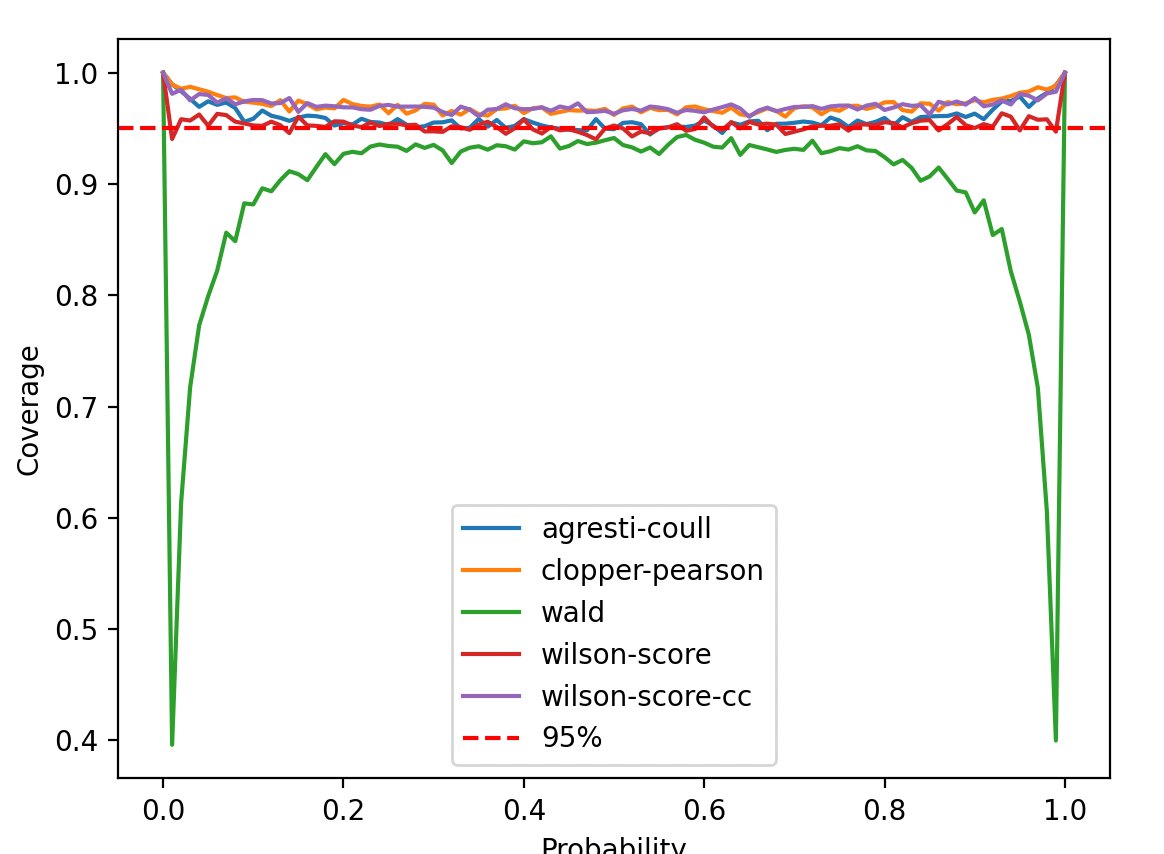
Wald intervalは被覆率が極端に低く、論外であることがわかる。p=0.5付近はまだマシとはいえカタログスペックを下回っており散々な結果だ。グラフを見やすくするため、Waldは除外して改めてプロットする。

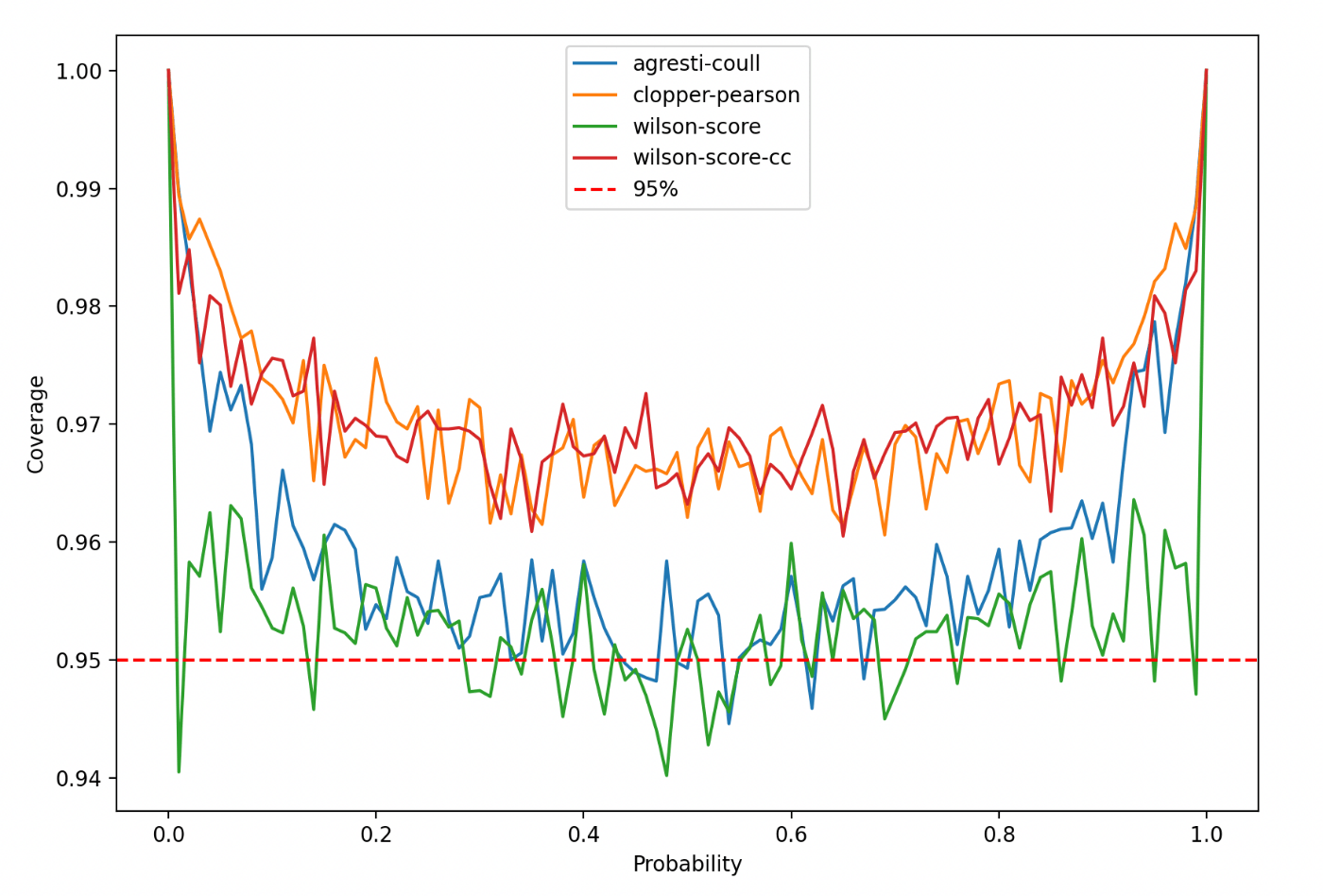
連続性補正付きWilson score法(wilson-score-cc)とClopper-Pearson法は全域で95%を上回っており優秀そうだ。残りの二つも極端に下回るということはなく、実用的な方法と言えるだろう。

だが、ちょっと待ってほしい。被覆率だけで評価すると、常に[0,1]を返すのが最善という結論にならないだろうか。もちろんそんなわけはなく、信頼区間は的が絞れていた方が嬉しいものである。
これを加味するため、信頼区間の幅を考慮して評価してみる。

詳細な説明は割愛するが、信頼区間の幅(上限 - 下限)の2乗と試行回数の積は一定の値に漸近することがわかっている。この積の平均値を、どのくらい的が絞れているかの指標とし、先ほどと同じ条件でアルゴリズムおよび確率ごとにプロットすると以下のようになる。

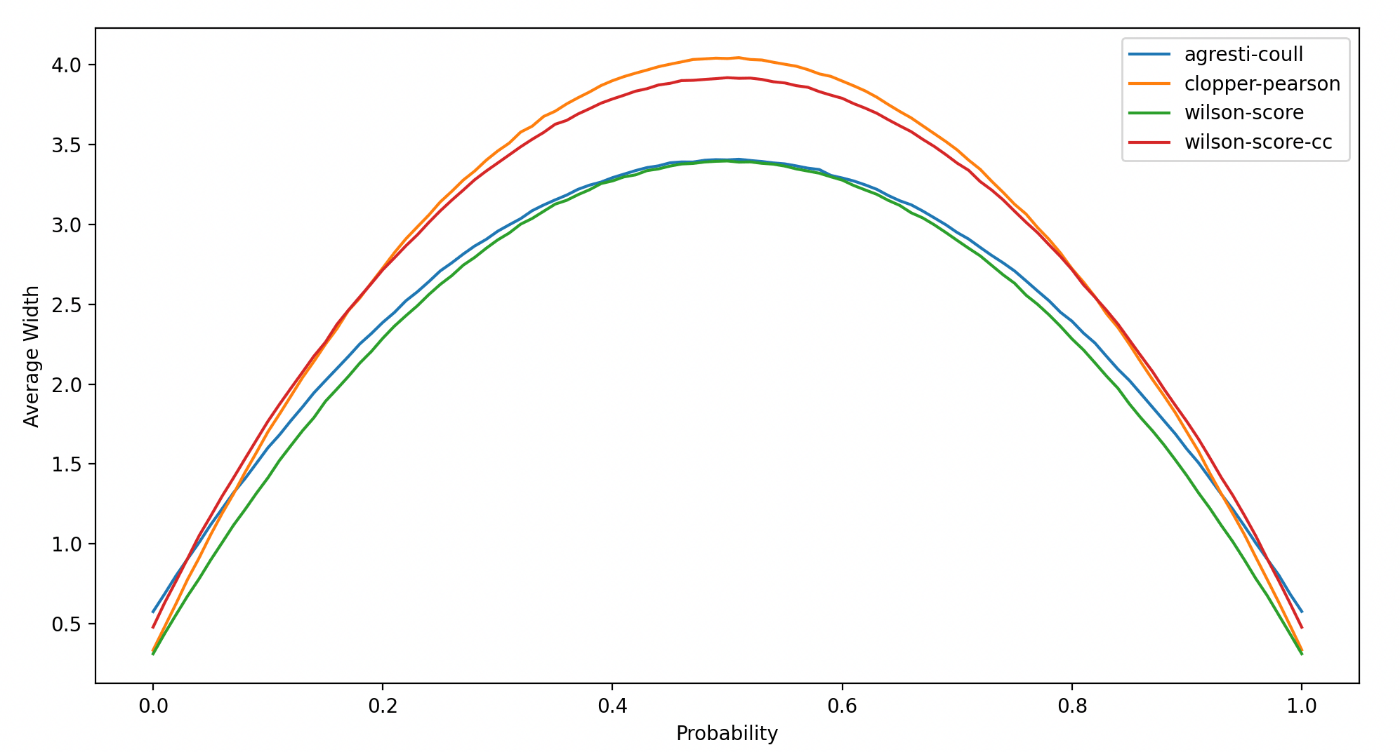
一見優秀なClopper-Pearson法および連続性補正付きWilson score法だが、信頼区間を広めに取ってしまうという欠点があるようだ。
Wilson score法は、被覆率が下振れしがちな代わり、全域にわたりよく絞れている。ビジネスシーンでの意思決定など、迅速な判断が求められる場合はこちらの方が都合が良さそうだ。

応用例

SLOconf 2021: Using Binomial proportion confidence intervals to reduce false positivesでは、エラーレートを単純に閾値と比較するのではなく、信頼区間を使うことにより、偽陽性のアラートを防ぐという応用が紹介されている。リクエスト数の少ない深夜にたまたまエラーが発生しても、信頼区間が広いので本当にエラー率が高いとは限らない(のでアラートを出さない)という判断ができる。

https://www.youtube.com/watch?v=R4nCsgt1qEU

DatadogのMonitorはカスタム数式が使えるので筆者も試してみようとしたが、平方根に対応しておらず、残念ながら採用できなかった。

まとめ

日常生活において、試行数と成功数がわかっており、そこから成功率を知りたい・比較したいケースはありふれている。各試行の成功率が一定かつ試行が独立しているとは限らないので過信は禁物だが、少なくともナイーブに割合を比較するよりは賢い判断ができる。
信頼区間の算出方法をいくつか紹介したが、計算しやすさと性能のバランスが良いWilson score intervalが無難な選択であるという印象を受けた。そして、Wald intervalは使ってはいけない。

実装

今回、評価に用いたコードは以下のGitリポジトリにまとめた。

https://github.com/fumieval/binomial-confidence-interval

PR

株式会社HERPは有意な成長をもたらしていただける仲間を募集しています。

https://herp.careers/v1/herpinc/zVEuWwkjSuW5

脚注

1. ここで「95%の"""確率"""で真の値を含んでいる」のような言い方をしてはいけない。信頼区間警察が飛んできて両側からエラーバーで殴られることになる

2. Alan Agresti & Brent A. Coull (1998) Approximate is Better than “Exact”
   for Interval Estimation of Binomial Proportions, The American Statistician https://math.unm.edu/~james/Agresti1998.pdf

3. ここで被覆確率の信頼区間を求めることもできるが、その信頼区間を求めるためにどの方法を使うかという議論が堂々巡りしてしまうため、ここでは触れない