😅

CS放浪記　〜ヘッド再帰と末尾再帰(1)〜

2021/09/06に公開

はじめに

こんにちは。ひろです。CS放浪記へようこそ！
今回も「再帰」について扱います。前回は、再帰が内部的にどのような動きをしているのかについて話しました。関数を呼ぶたびに関数と計算に必要な変数などをコールスタックにPUSHし、関数の評価が終わるとPOPされる仕組みを使って再帰が実現されていることを見ていきました。今回からは2回に分けて、再帰を最適化するための方法について見ていきます。前回見た再帰関数が、実はメモリにとってかなり負担が大きいことをみていきましょう！

再帰の種類

まずは再帰には種類があることを紹介しておきます。再帰には以下の2種類存在します。

ヘッド再帰
末尾再帰

それぞれ見ていきましょう。ヘッド再帰とは「戻り値の評価が完了する前に、次の関数を呼び出す再帰」のことです。前回みたminmin関数がまさにこれです。"ミン" + minmin(count-1)の評価が完了する前にminmin(count-1)関数を呼び出し、コールスタックに関数が積まれていっていましたよね。このようにコールスタックにどんどん関数を積み上げていく再帰がヘッド再帰です。以下にヘッド再帰の例を記載しておきます。コードの詳細は前回の記事に詳しく記載していますのでご参照ください。

package main

import "fmt"

func minmin(count int64) string {
	if count <= 0 {
		return "ミーン"
	} else {
		return "ミン" + minmin(count-1)
	}
}

func main() {
	fmt.Println(minmin(3)) // ミンミンミンミーン
}

上の再帰に対して、「戻り値の評価が完了してから、次の関数を呼び出す再帰」が存在します。それが末尾再帰です。これは呼び出された関数が評価され、その返却値が次の関数の引数になるような再帰関数です。コードの例を見て書き方を見てみましょう。

package main

import "fmt"

func minmin(count int64, cry string) string {
	if count <= 0 {
		return cry + "ミーン"
	} else {
		return minmin(count-1, cry+"ミン")
	}
}

func main() {
	fmt.Println(minmin(3, ""))
}

変わったところは、関数の引数が増えているところです。鳴き声を表すcryに鳴き声を追加した結果を次に呼び出す関数の引数としています。それ以外では、ベースケースに入った場合、ヘッド再帰では"ミーン"だけを返すようにしていましたが、末尾再帰ではcry + "ミーン"になっています。これは今までの鳴き声がcryの中に入っているので、今までの鳴き声に"ミーン"を足した結果を返すようになっています。

どっちを使ったらいいの？

2種類の再帰があることがわかったところで、どちらを使ったほうがいいか疑問に思うんじゃないかと思うので、私の見解を書きたいと思います。私の見解として、末尾再帰を使って欲しいと思います。理由は以下に記載します。

末尾再帰の方が計算量が少なくなる
末尾再帰はスタックメモリを1つしか使わないため、スタックオーバーフローの発生を防ぐことができる

この記事では、ヘッド再帰だとなぜ上の2点が問題になるかをみていきます。

末尾再帰の方が計算量が少なくなる

一部の再帰において、計算量が少なくなります。ここでいう計算量とは、時間計算量で、問題を解くまでに必要な手順の回数を指します。計算量が少なくなる例として、フィボナッチ数列を実装してみましょう。フィボナッチ数列とは、0と1から始まる数列のことで、前の2つの数字を足した結果が次の数になるような規則性を持った数列です。定義を書くと以下のようになります。
n = 0の時、 $F_0 = 0$
n = 1の時、 $F_1 = 1$
n >= 2の時、 $F_n = F_{n-1} + F_{n-2}$

まずはフィボナッチ数列の計算に慣れる

1~5番目のフィボナッチ数列の計算に慣れましょう。フィボナッチ数列は「0と1から始まる数列」なので、数列の1番目と2番目はそれぞれ0、1が入ります。今の数列の状態は以下です。左側の数字は数列の位置です。

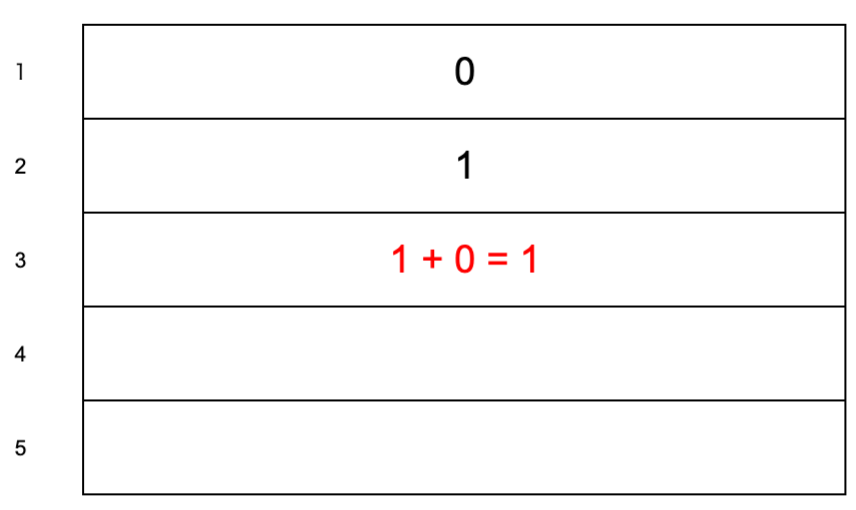
それでは3番目の数字をみていきましょう。フィボナッチ数列は、 $F_n = F_{n-1} + F_{n-2}$ の計算結果になります。今回は $F_{n-1} = 1$ 、 $F_{n-2} = 0$ なので、0 + 1の計算結果である「1」が3番目に入ります。

次は4番目の数字を見ていきましょう。 $F_{n-1} = 1$ 、 $F_{n-2} = 1$ なので、1 + 1の計算結果である「2」が4番目に入ります。

最後に5番目の数字を見ていきましょう。 $F_{n-1} = 2$ 、 $F_{n-2} = 1$ なので、2 + 1の計算結果である「3」が5番目に入ります。

これがフィボナッチ数列です。計算のイメージがついてきましたでしょうか？

フィボナッチ数列を実装する

おおよその計算イメージがついたところで、実際にコードを書いてみましょう。まずはヘッド再帰で書いてみます。以下のパターンを忠実に再現します。
n = 0の時、 $F_0 = 0$
n = 1の時、 $F_1 = 1$
n >= 2の時、 $F_n = F_{n-1} + F_{n-2}$

package main

import (
	"fmt"
)

func fibonacciHead(count int64) int64 {
	if count == 0 {
		return 0
	} else if count == 1 {
		return 1
	} else {
		return fibonacciHead(count-1) + fibonacciHead(count-2)
	}
}

func main() {
	fibonacciHead(5)
}

これは前回見た再帰と同じ方法です。再帰呼び出しのたびにコールスタックに新しく関数が追加され、全ての関数が呼ばれた後に返ってきた値を逐一計算していきます。また、この関数は、ベースケースでない時、2つの関数を返します。それぞれの関数がベースケースを終えるまで再帰が繰り返されます。コールスタックがどうなっているのか確認してみましょう。
fibonacciHead(5)で考えてみましょう。引数が5なので、fibonacciHead(4) + fibonacciHead(3)が返ってきます。

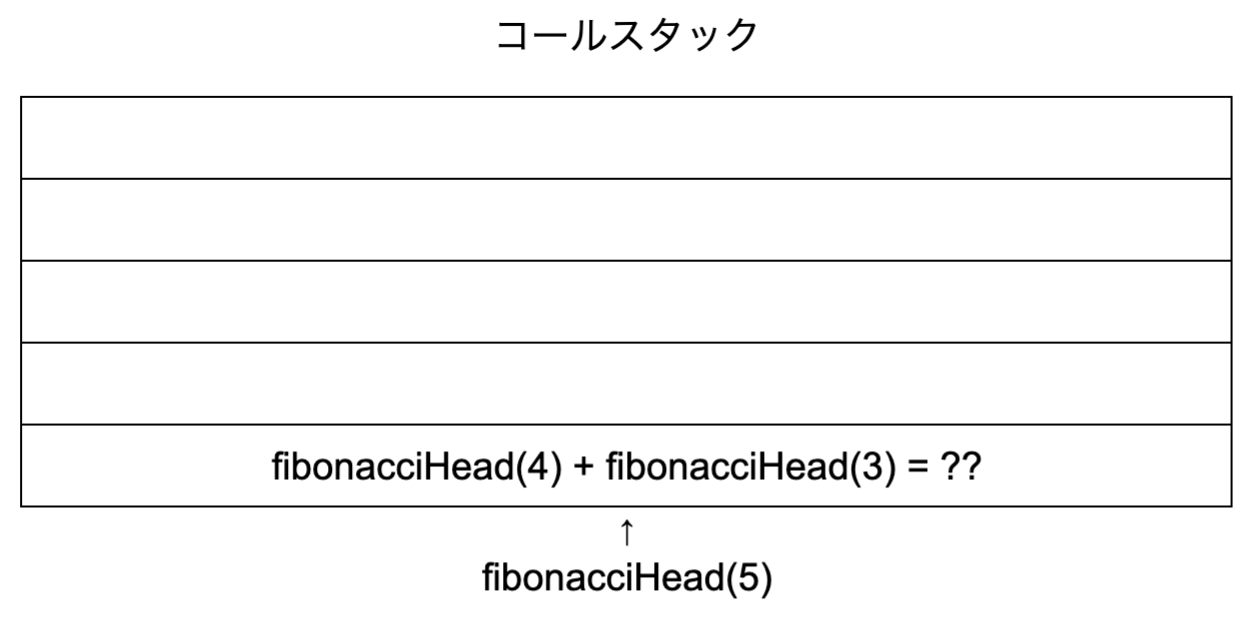
次に実行されるのはfibonacciHead(4)です。関数の方が演算子よりも優先度が高いため、そうなります。fibonacciHead(4)は引数が4なので、fibonacciHead(3) + fibonacciHead(2)が返ってきます。

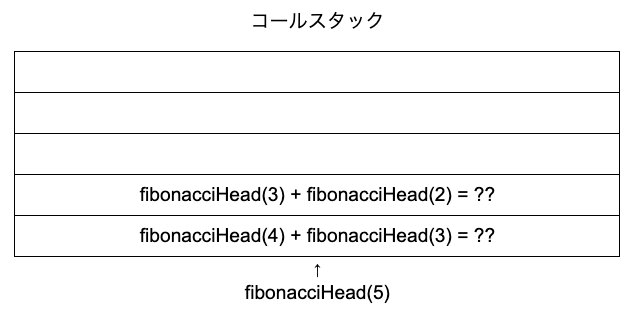
またまた関数が存在するため、fibonacciHead(3)を次に実行されます。引数が3なので、fibonacciHead(2) + fibonacciHead(1)が返されます。

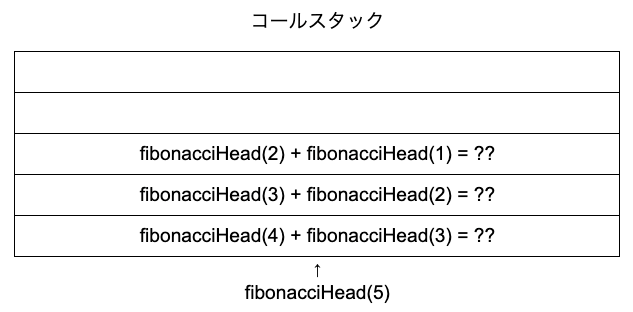
関数が存在するため、fibonacciHead(2)を先に実行されます。引数が2なので、fibonacciHead(1) + fibonacciHead(0)が返されます。

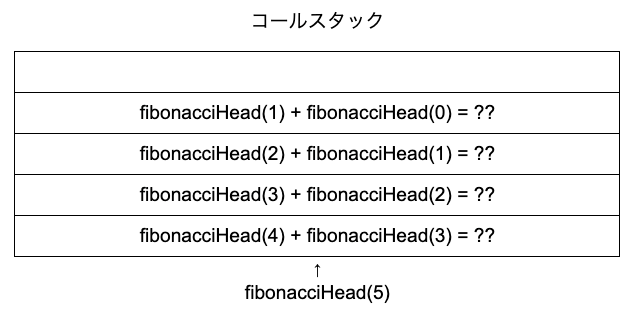
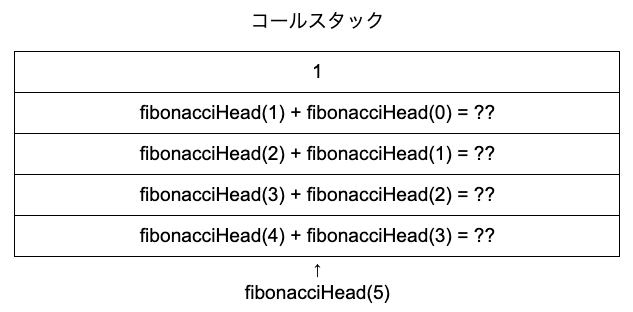
fibonacciHead(1)を実行します。引数が1なので、1が返されます。ついにベースケースに到達しました。

コールスタックの一番上にある「1」はすでに評価済みのため、POPされます。POPされた値は、fibonacciHead(1)に代入されます。

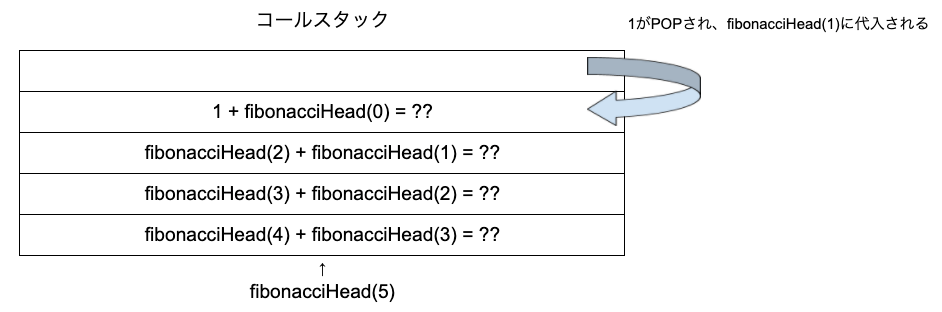
この後は何が実行されるでしょうか？答えはコールスタックの一番上に積まれているfibonacciHead(0)です。コールスタックは上に積まれている順に実行され、かつ関数が優先的に実行されるためです。引数が0なので0を返します。

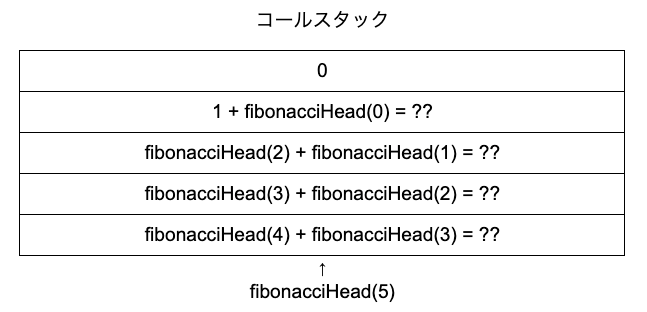
コールスタックの一番上にある「0」はすでに評価済みのためPOPされ、fibonacciHead(0)に「0」が入ります。よって、fibonacciHead(1) + fibonacciHead(0)は $1 + 0 = 1$ となります。

今回の計算結果は、fibonacciHead(2)が呼び出した関数の計算結果であるため、fibonacciHead(2)には「1」が入ります。また、fibonacciHead(1)は先ほど見た通り「1」なので、fibonacciHead(2) + fibonacciHead(1)は $1 + 1 = 2$ になります。

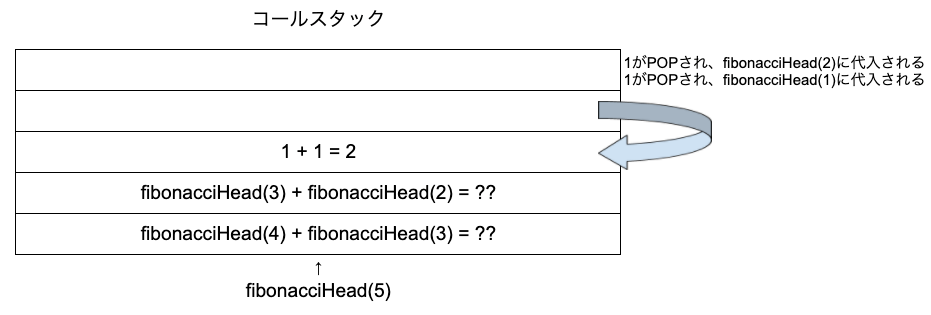
これで、fibonacceHead(3)の実行結果が2になることがわかりました。fibonacceHead(3) + fibonacciHead(2)については、fibonacceHead(3)に先ほどの計算結果の2を代入し、fibonacceHead(2)には1を代入することで $2 + 1 = 3$ が計算結果となります。

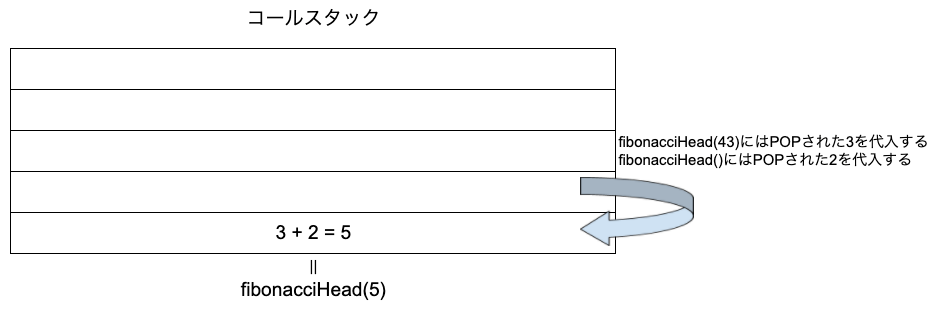
仕上げにfibonacceHead(4) + fibonacciHead(3)を計算しましょう。fibonacceHead(4)には先ほど計算した3を代入し、fibonacciHead(3)には2を代入することで $3 + 2 = 5$ が計算結果となります。これがfibonacciHead(5)を実行した結果です。

処理の大まかな流れを確認しました。かなり複雑な再帰で頭がこんがりそうになると思いますが、何度か計算過程を紙に書くと動きが理解できるようになるので頑張ってみてください！

どれだけ関数呼び出しがあったのか

フィボナッチ数列の実装と簡単な処理の流れを説明したので、実際どれだけの関数呼び出しがあったのかをみていきましょう。説明するときは端折ったのですが、fibonacciHead関数は、ベースケースであるfibonacciHead(1)またはfibonacciHead(0)が呼ばれるまで再帰を繰り返します。なので、この関数は木構造を使うことでどれだけ関数の呼び出しがあるかを可視化することができます。実際にfibonacciHead(5)が呼ばれた時に呼び出される関数の引数を木構造として表したのが以下です^[1]。

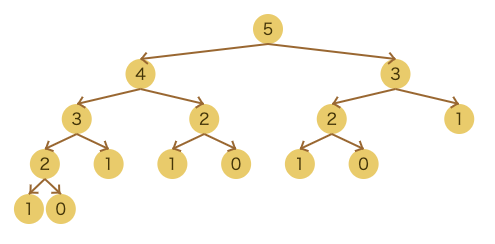
こう見るとわかるのですが、全ての関数が0または1になるまで再帰呼び出しを繰り返しています。なのでびっくりするぐらい効率が悪い処理になります。実際どれだけ効率が悪いのかを確認するために、ベンチマークを回してみましょう。Goには標準ライブラリでベンチマークを提供しているので、これを使用します。
ベンチーマークを回すために新しくコードを書きましょう。「main_test.go」というモジュールを作成し、以下のように記述します。今はコードの中身を理解しなくて大丈夫です^[2]。

package main

import "testing"

func BenchmarkFibonacciHead(b *testing.B) {
	fibonacciHead(5)
}

さて、実行してみましょう。私の環境^[3]で実行した結果、以下が出力されました。

% go test -bench=.          
goos: darwin
goarch: arm64
pkg: main
BenchmarkFibonacciHead-8   	1000000000	         0.0000002 ns/op
PASS
ok  	tour	0.236s

fibonacciHead(5)を実行したら平均0.0000002 ns/opかかることがわかりました。次は、引数を10倍して実行してみようと思います。単純に考えると引数が10倍になったので計測結果も10倍だけ増えると予想できますが、実際はどうでしょうか？実行した結果は以下です。

% go test -bench=.
goos: darwin
goarch: arm64
pkg: main
BenchmarkFibonacciHead-8   	       1	116987893875 ns/op
PASS
ok  	tour	117.364s

とてつもなく秒数が増えているのがわかると思います。Goのベンチマークではナノ秒で表示されているので、秒数に変換すると約116秒となります。fibonacciHead(5)を実行したときと比べて10倍どころか $10^18$ くらいに増えています。

おわりに

今回は、ヘッド再帰について見てみました。関数が呼ばれるたびにコールスタックに関数が積まれていき、最終的には効率の悪い結果となりました。「これならfor文の方がよくね？」と思う方もいると思いますが、安心してください。ちゃんと対策があります。
次回は対策として、末尾再帰について解説します。この方法を使うことで先ほど見た絶望的に遅いフィボナッチ数列を高速化できるので楽しみにしてください！
それではまたお会いしましょう！アディオス！

脚注

以下のライブラリを使うことで簡単に木構造が可視化できます。使い方もとても簡単ですごいです。。。
https://www.npmjs.com/package/tree-visualizer ↩︎
Goのベンチマークの使い方については以下をご参照ください。
https://pkg.go.dev/testing ↩︎
私が使っている端末はM1MacBook Airです。 ↩︎