🔖
量子コンピューティングことはじめ
概要
- 量子コンピューティングを行う上での基礎的な内容をまとめてみました。
アダマールゲート(Hadamard Gate)
- 単一量子ビットを重ね合わせ状態に変換
- 行列表現:

- 例:
グローバーのアルゴリズム(Grover's Algorithm)
-
目的:最小回数で正解を見つける探索アルゴリズム(O(√N))
-
流れ:
- アダマールで全状態を重ね合わせ
- オラクルで正解の符号を反転
- 拡散演算(反転増幅)
- 測定
-
Python(Qiskit)での例あり
CNOTゲートとSWAPゲート
🔹 CNOT(制御NOT)
- 制御ビットが1のときだけターゲットビットを反転
🔹 SWAP
- 2ビットの状態を完全に交換
- CNOT 3つで構成可能
テンソル積(Tensor Product)
- 複数の量子ビットを1つの状態にまとめる演算
例:
エンタングル状態(量子もつれ)
- テンソル積で分解できない量子状態
例:ベル状態(最大エンタングル)
[
|\Phi^+⟩ = \frac{1}{\sqrt{2}} (|00⟩ + |11⟩)
]
量子フーリエ変換(QFT)
-
位相情報から周期性を取り出す量子版フーリエ変換
-
応用:Shorのアルゴリズム、位相推定など
-
構成要素:
- アダマール
- 制御回転ゲート(Rₖ)
- SWAP(ビット順反転)
QAOA(量子近似最適化アルゴリズム)
-
組合せ最適化を量子回路で近似解探索
-
流れ:
- 初期状態(アダマール)
- 問題ハミルトニアン ( H_C )
- ミキサーハミルトニアン ( H_M )
- パラメータ最適化(古典)
量子アニーリング
- エネルギーの低い状態に「なだれ落ちる」ように解を探索
- 量子トンネル効果を活用
- 代表例:D-Waveマシン
ハミルトニアン(Hamiltonian)
- 量子系の全エネルギーを表す演算子
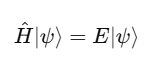
- 観測対象(エネルギー、位置など)すべてを含む
スピン多重度(Spin Multiplicity)

| 状態名 | S | 多重度 | 例 |
|---|---|---|---|
| シングレット | 0 | 1 | ↑↓ |
| ダブレット | 1/2 | 2 | ↑ |
| トリプレット | 1 | 3 | ↑↑ |
- スピン系のハミルトニアン (イジングモデル)

エルミート演算子(Hermitian Operator)
- 自分の共役転置と等しい演算子:

-
特徴:
- 固有値はすべて実数
- 観測に使われる演算子はすべてエルミート
VQE(変分量子固有値ソルバー)
-
基底状態のエネルギー(最小固有値)を求めるための量子・古典ハイブリッドアルゴリズム
-
流れ:
- パラメータ付き量子状態 ( |\psi(\theta)⟩ ) を準備
- エネルギー期待値を量子回路で測定
- 古典的にパラメータ ( \theta ) を最適化
VQEとQAOAの違い
| 項目 | VQE | QAOA |
|---|---|---|
| 目的 | 固有値最小化(基底状態) | 組合せ最適化の近似解 |
| 回路 | パラメータ付き状態(ansatz) | 問題ハミルトニアン+ミキサー |
| 主な応用 | 量子化学 | グラフ・割当最適化など |

Discussion