Linear Transformerについて

Transformerの実行速度の高速化は、GPUメモリ効率化由来のFlashAttentionなどの手法が主流です。
逆にモデルの論理的面での高速化手法はないかと思い調査し、見つけた内容です。

どんな技術か

• Attentionは、トークン系列長に大きく影響を受ける計算時間をしている。
  • Attentionでは、２つの系列(１つの系列同士でも可)間ですべての系列番号の組み合わせで特徴次元数分の内積計算を実行する。
    Attentionの計算時間は、系列長×系列長×特徴次元数に比例するため$O(系列長^2×特徴次元数)$となる。
• 深層学習では様々なデータを扱うが、音楽や文章等で非常に系列長が長いデータを扱う際に、通常のAttentionでは計算時間が莫大に増えるため、学習・推論時間の爆発的増加を引き起こすことになってしまう。
• Linear Transformerでは、Attentionの計算時間を計算上の工夫を施すことで、系列長に対して計算時間が線形的に増加するように改良をしたものである。

どのような利点があるか

• 通常のAttentionに比べ、長い系列長のデータでの学習の際に学習時間が短縮できる。
• 長い文章の生成の際に、時間がかかりにくくなる。

どのような場面で役に立つ技術か

• 音楽データを扱う深層学習モデルの開発
• 長い文章に対応できる言語モデルの開発
• 解像度の大きな画像を利用したモデルの開発

どのような技術が使用されているか

カーネルトリック

• 2つのベクトルの写像後のベクトルの内積計算を別の類似関数に置き換えること。
• 本来は写像関数が明示的にわからなくても類似関数で代用し計算可能にする手法。
• 今回の論文では、カーネルトリックを式変形に使用し、計算時間の低減に利用している。
• 数式で書くと以下の形になる。
  
  $$\mathrm{sim}(\bold{x}_1,\bold{x}_2) = \phi(\bold{x}_1)\phi(\bold{x}_2)$$
  
  $\bold{x}_1,\bold{x}_2$:ベクトル
  $\phi$:写像関数 (ある空間のベクトルを別の空間のベクトルに変化させるイメージ。特徴量の次元数を変更する等がわかりやすいかも)
  $\mathrm{sim}( \cdot , \cdot)$:類似関数(カーネル関数)

TransformerのAttention(Scaled-Dot Product Attention)に対するカーネルトリックの適用

Scaled-Dot Product Attention(通常のAttention)

$$\mathrm{Attention}(Q,K,V) =\mathrm{softmax} \left( QK^{\mathsf{T}} \over \sqrt{d} \right)V$$

$$\begin{split} \mathrm{Attention}(Q,K,V)_i &= {\sum^{n}_{j=1} \mathrm{softmax} \left({\bold{q}^{\mathsf{T}}_i\bold{k}_j \over \sqrt{d}} \right) \bold{v}^{\mathsf{T}}_j} \\ &= {\sum^{n}_{j=1} \mathrm{exp} \left({\bold{q}^{\mathsf{T}}_i\bold{k}_j \over \sqrt{d}} \right) \bold{v}^{\mathsf{T}}_j \over \sum^{n}_{j=1} \mathrm{exp} \left({\bold{q}^{\mathsf{T}}_i\bold{k}_j \over \sqrt{d}} \right)} \end{split}$$

クエリ:$Q = (\bold{q}_1,\bold{q}_2,...,\bold{q}_m )$ $\bold{q}_i = (q_1, ... , q_d)^{\mathsf{T}}$　$Q$のサイズ $m\times d$
キー:$K = ( \bold{k}_1,\bold{k}_2,...,\bold{k}_n )$ $\bold{k}_i = (k_1, ... , k_d)^{\mathsf{T}}$　$K$のサイズ$n\times d$
バリュー:$V = ( \bold{v}_1,\bold{v}_2,...,\bold{v}_n )$ $\bold{v}_i = (v_1, ... , v_d)^{\mathsf{T}}$　$V$のサイズ $n\times d$
※self-Attentionの時$m=n$
$i = 1,2,3,...,m$

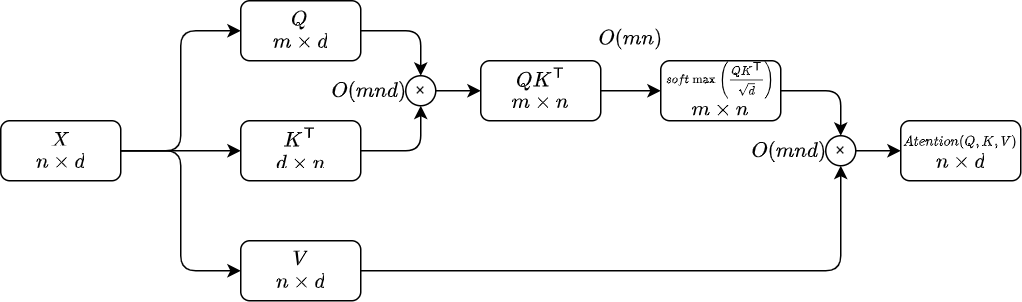
Attentionのアーキテクチャ

計算時間は、$O(mnd)$となり、系列長×系列長×特徴次元数に比例する。
特徴次元数はモデルにより一定の値を取るため、計算時間は系列長の2乗に従い変動する。

カーネルトリックを適用したScaled-Dot Product Attention

$\mathrm{sim}(\bold{q},\bold{k}) = \mathrm{exp} \left({\bold{q}^{\mathsf{T}}_i\bold{k}_j \over \sqrt{d}} \right)$とし、$\phi \coloneqq \mathbb{R}^{d} \to \mathbb{R}^{l}$としたとき、Attentionの式は以下のようになる。

$$\begin{split} \mathrm{AttentionKT}(Q,K,V)_i &= {\sum^{n}_{j=1} \mathrm{sim} \left(\bold{q}_i,\bold{k}_j \right) \bold{v}^{\mathsf{T}}_j \over \sum^{n}_{j=1} \mathrm{sim} \left(\bold{q}_i,\bold{k}_j\right)}\\ &= {\sum^{n}_{j=1} \phi(\bold{q}_i)^{\mathsf{T}} \phi(\bold{k}_j) \bold{v}^{\mathsf{T}}_j \over \sum^{n}_{j=1} \phi(\bold{q}_i)^{\mathsf{T}} \phi(\bold{k}_j)} \\ &= { \phi(\bold{q}_i)^{\mathsf{T}} \sum^{n}_{j=1} \phi(\bold{k}_j) \bold{v}^{\mathsf{T}}_j \over \phi(\bold{q}_i)^{\mathsf{T}}\sum^{n}_{j=1}\phi(\bold{k}_j)} \end{split}$$

Linear Transformerのアーキテクチャ
計算時間は、$O(mld)$または$O(nld)$となり、系列長×特徴次元数×写像後特徴次元数に比例する。
特徴次元数、写像後特徴次元数はモデルにより一定の値を取るため、計算時間は、系列長により変動する。

写像関数について

• Linear Transformerの元論文では、$\phi$にELU関数を利用している。
• ELU関数(exponential linear unit function)

$$\phi(x) = \begin{cases} x &\text{if } x \gt 0 \\ \alpha (\mathrm{exp}(x)-1) &\text{if } x \le 0 \end{cases}$$

課題点は何か

• 精度が通常のAttentionより若干低くなる。
  • 論文内では、画像補完タスクや音声認識タスクの結果を提示しているが、どれも結果が通常のAttentionに劣る性能をしている。

参考文献

元論文
Transformers are RNNs:Fast Autoregressive Transformers with Linear Attention
参考記事
TransformerのAttentionの線形化による計算量削減【Linear Transformer】
カーネル法とカーネルトリックを図を用いて解説する