テンソルネットワークによるMLP圧縮① -テンソルネットワークとは-

こちらの記事にテンソルネットワークを使ったディープラーニングのパラメータ削減のチュートリアルがあり、興味深かったため忘備録として理解できたことをまとめていきたいと思います。今回は、テンソルネットワークとは何かという点について説明します。

テンソルとは

テンソルはベクトルや行列の考え方を拡張した概念です。ベクトルは1次元の方向に値が並んだもので、行列は行と列の2次元の方向に値が並んだものになります。これを一般化したものがテンソルであり、テンソルを導入することで3次元以上のケースについても取り扱うことができます。ちなみに、ベクトルは1階のテンソル、行列は2階のテンソル、スカラーは0階のテンソルと言い換えることもできます。

テンソルネットワークとは

ベクトルの内積や行列同士の積など、テンソル同士の計算を扱いやすくするための手法という理解です。ここでは、テンソルネットワークの計算方法の概要について、簡単に説明します。
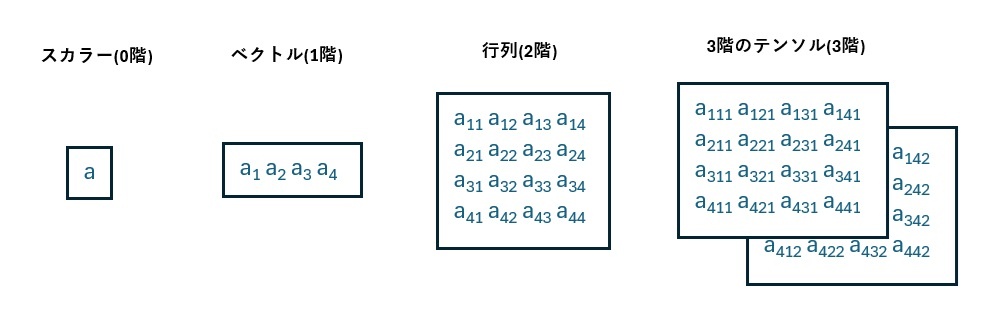
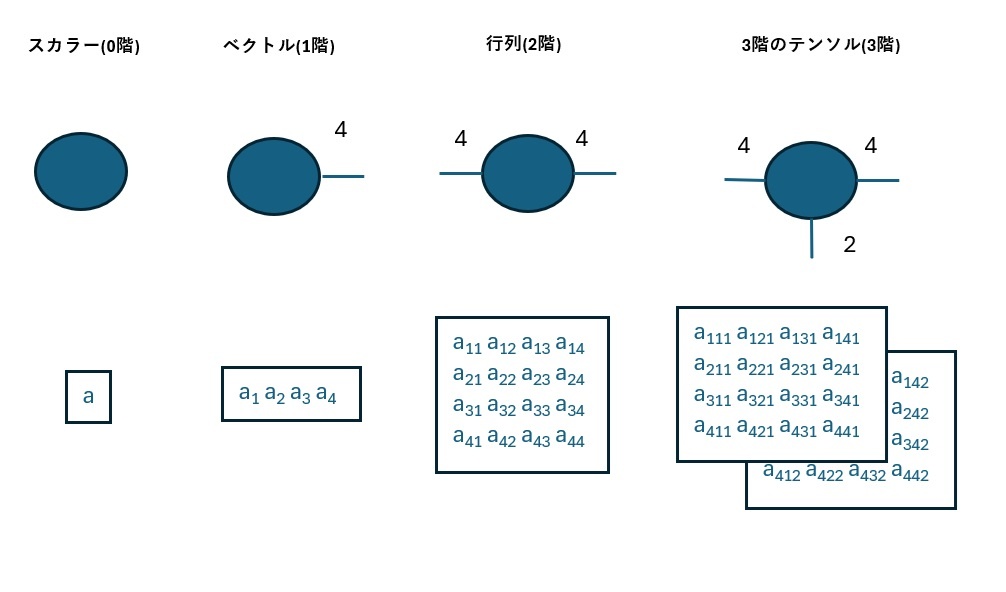
ベクトルや行列などのテンソルを、テンソルネットワークを使って図示化すると、以下のように丸に足が生えたようなものになります。(厳密なルールは無く、図形は丸でなくても何でも良いです)
ここで、足の数はテンソルの階数を表しており、各足の付近の数字は次数を表しています。
例えば、ベクトルは1階のテンソルなので足の数は1本であり、以下の例では次数(要素の数)は4であるため、添え字の4は次数4のベクトルであることを示しています。行列については、2階のテンソルであるため足が2本あり、以下の例では4行4列の行列であるため、各足の添え字は4になります。
同様のルールで以下のテンソル(3階のテンソル)についても各足の添え字は各次元の次数を表しており、テンソルの全要素数は添え字の積によって求めることが出来ます。
(3階テンソルの例では、要素数は4×4×2=32)

テンソルネットワークの計算例

馴染みのある例として、ベクトルの内積計算をテンソルネットワークで考えてみます。
以下の様に、次数4のベクトルaとbの内積を考えると、ベクトルの内積はスカラー値となり、テンソルネットワークでは以下の様に書くことが出来ます。

ここで、テンソルネットワークの表現では、各ベクトルの1本の足同士がまとめられて1つになっています。これが内積計算を表しており、テンソルネットワークでは「縮約」といいます。内積の計算規則になりますが、ベクトルの次数が同じもの同士でしか計算することが出来ず、テンソルネットワークの縮約においても足の次数が同じである必要があります。

これだけではテンソルネットワークのメリットがあまりわからないのですが、別の見方をすると、縮約によって足の数が減り、計算後には外向きの足の数が0なるという点について、以下の様に図から視覚的に理解することができます。

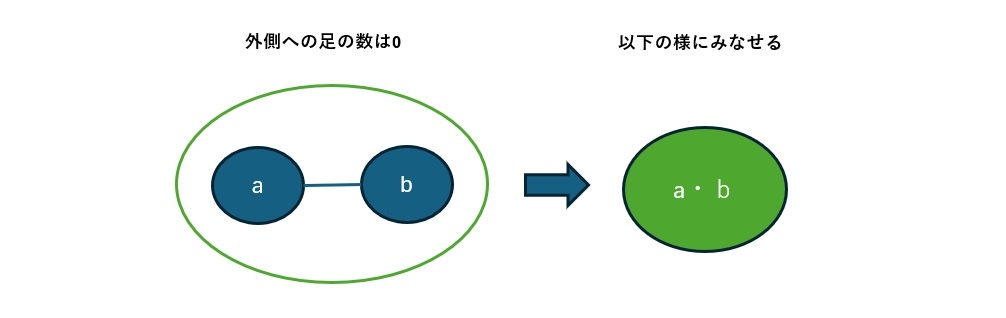
このことは何を示しているかというと、ベクトル(1階のテンソル)同士の縮約(内積)によって、スカラー(0階のテンソル)が生成されるということであり、実際に計算を行わなくてもテンソルの階数や要素数の遷移がわかるというところが、テンソルネットワークの便利な点となります。

行列の積についてもテンソルネットワークを適用してみると、行列の積は行列であることが、以下の様に視覚的に理解することができます。(かつ、行と列の次数が同じ場合しか計算ができないということが縮約のルールとして表れています)

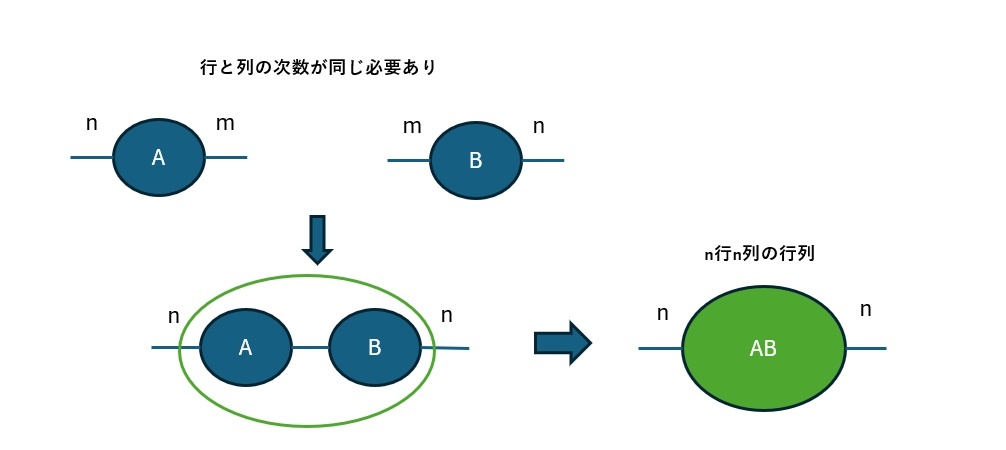
行列の積が行列になるということについては、特にテンソルネットワークを使わなくても明らかかもしれませんが、それ以上の階数のテンソルを扱う際に、テンソルネットワークは効果を発揮します。
例えば、3階のテンソルとベクトルの積については、以下の通り結果が行列となることが、テンソルネットワークを使うと簡単に求められます。

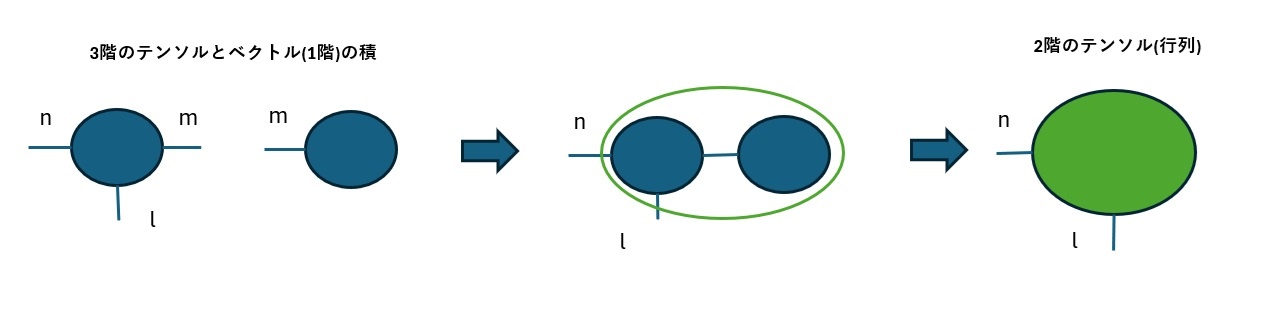
縮約について

ベクトルの内積や行列同士の積について、テンソルネットワークの文脈で見ると、同じ縮約という操作になるということがわかりました。ベクトルの内積や行列の積の積算は、それぞれ別の演算として数学では習った記憶がありますが、本質的には同じもの(成分同士の積の和)になります。

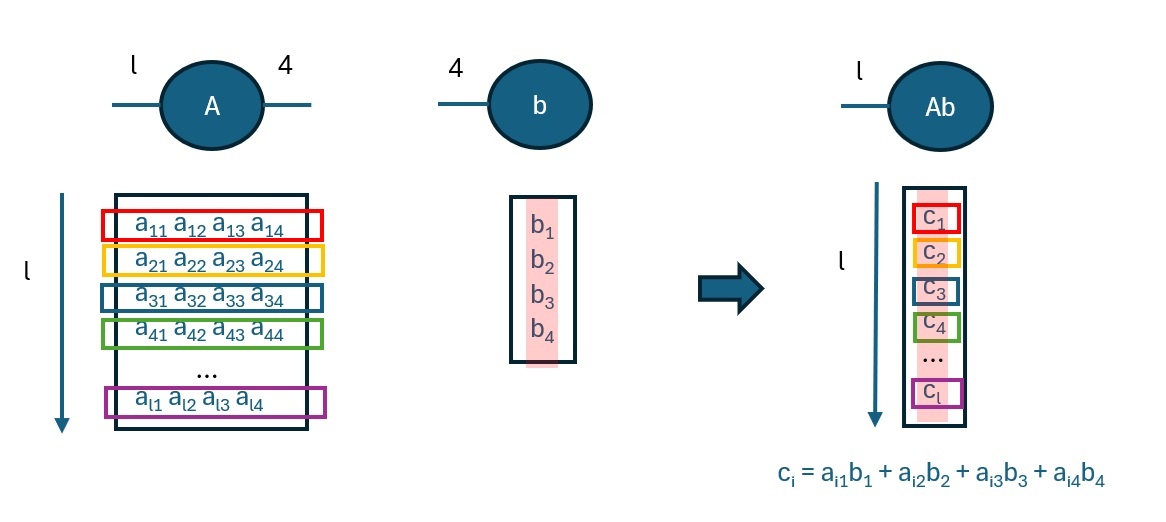
以下の図のように、l行m列の行列と次数mのベクトルの縮約を考える際に、行列側は次数mのベクトルがl組あるとみなすことができ、m次のベクトル同士の内積操作をl回取ると考えることが出来ます。そうすると、最終的にはl個のスカラー値が出力されるので、結果は次数lのベクトルになるという見方をすることが可能です。(図ではm=4)

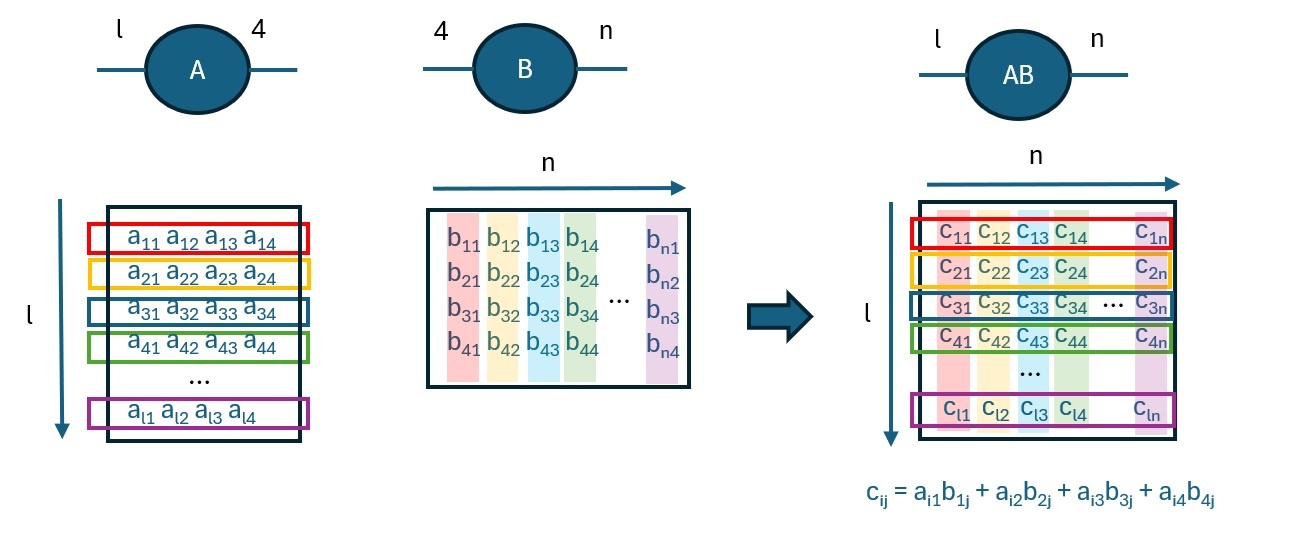
考えを行列の積に拡張して、縮約の相手がm行n列の行列であった場合でも、上記のベクトルの場合の縮約の操作が、行列として拡張された次数mの分だけ繰り返されることになりますが、本質的には同じ縮約の操作の繰り返し(次数mのベクトルの内積演算)になります。

どうやってMLPの圧縮に使うのか

タイトルの通り、テンソルネットワークを使ってディープラーニングの全結合層のパラメータ数の削減をするチュートリアルの解説を行うことが目的ですが、今回はテンソルネットワークの説明が長くなってしまったので、チュートリアルの解説は次回の記事で行います。どのようにテンソルネットワークを圧縮に活用するかという概要ですが、ディープラーニングの重み伝搬を行列計算していた部分をテンソルネットワークに置き換えることで、パラメータ数(重みの数)を削減することができる、という方針になります。(次回に続きます)