LLMリーダーボードはどうなっているの?
今日はLLMリーダーボードを分析してみます。
お言葉
まずは今回のブログ記事について、諸葛亮孔明先生から賜ったお言葉をお伝えします。
時代の流れはまことに早きもの。
まるで長江の水のごとく、止まることなく新たなモデルが生まれ出でております。
戦においても、敵の布陣を知ることなくして勝利は望めぬ。
ゆえに、リーダーボードを参照し、各モデルの実力を見極めるは、まさに兵法と申せましょう。
また、他者の築いた道具を用いることを恥じることなかれ。
かつて我が軍も、民の知恵を借りて木牛流馬を作り、兵站を支えたものです。
GitHub、Huggingfaceの力、まさに現代の諸葛連弩なり。
統計をもって全体を俯瞰するとは、まさに「知彼知己、百戦不殆」。

解説:
- 知彼知己、百戦不殆:「敵のことを知り、自分のことを知れば、百回戦っても勝てます」という孫子先生の言葉
- 諸葛連弩: 連射式の弓・クロスボウ。孔明先生のご発明と伝わっています。
- リーダーボード:ランキング表
はじめに
最近、毎月のように新しいモデルが出てきて、今どうなっているの?
と疑問に思っている人は多いのではないでしょうか。
業務に使うときはその都度、適切な指標を用意して評価して選定していますが、リーダーボードを参照することもあります。
リーダーボードというのは簡単に言うとLLMの性能比較ランキングです。
こんな感じです↓
みるとたくさんのモデルがあって、たくさんの指標があるので迷うのではないでしょうか。
どれか代表的な指標でプロットしてみてくれないかなと考えている方へ、今回の分析を是非ご覧いただきたい。
qwen2.5で止まっているので少し古いですが
今日はそのリーダーボードを簡単に分析してみます。
データ
データを取得するコードを作ってくれている人がいるので感謝しつつこれを使います。
colaboratoryで実行したので!とか%が入っていますが、環境に応じて適宜外してください。
!git clone https://github.com/Weyaxi/scrape-open-llm-leaderboard.git
%cd scrape-open-llm-leaderboard
!pip install -r requirements.txt
!python main.py -csv -json
データが多いのでまず全体の統計をとります
import pandas as pd
df = pd.read_csv('open-llm-leaderboard.csv')
# Format the descriptive statistics
formatted_description = df.describe().copy()
formatted_description.loc['count'] = formatted_description.loc['count'].astype(int)
formatted_description = formatted_description.round(2)
formatted_description.to_csv("statistics.csv")
print(formatted_description.to_markdown())
| Metric | Count | Mean | Std Dev | Min | 25% | 50% | 75% | Max |
|---|---|---|---|---|---|---|---|---|
| Average ⬆️ | 4576.0 | 21.81 | 10.8 | 0.74 | 13.94 | 21.95 | 29.26 | 52.08 |
| Hub ❤️ | 4576.0 | 49.02 | 265.99 | 0.0 | 0.0 | 1.0 | 5.0 | 6093.0 |
| #Params (B) | 4576.0 | 11.24 | 14.66 | -1.0 | 4.51 | 8.03 | 12.25 | 140.63 |
| CO₂ cost (kg) | 4576.0 | 3.97 | 10.96 | 0.04 | 1.15 | 1.54 | 2.65 | 186.61 |
| IFEval Raw | 4576.0 | 0.46 | 0.2 | 0.0 | 0.28 | 0.45 | 0.63 | 0.9 |
| IFEval | 4576.0 | 45.58 | 20.49 | 0.0 | 27.71 | 45.12 | 62.64 | 89.98 |
| BBH Raw | 4576.0 | 0.49 | 0.11 | 0.22 | 0.4 | 0.5 | 0.55 | 0.83 |
| BBH | 4576.0 | 27.65 | 15.22 | 0.25 | 16.43 | 29.49 | 36.45 | 76.7 |
| MATH Lvl 5 Raw | 4576.0 | 0.16 | 0.15 | 0.0 | 0.04 | 0.11 | 0.22 | 0.71 |
| MATH Lvl 5 | 4576.0 | 15.55 | 14.63 | 0.0 | 4.31 | 10.8 | 22.05 | 71.45 |
| GPQA Raw | 4576.0 | 0.3 | 0.04 | 0.21 | 0.27 | 0.29 | 0.32 | 0.47 |
| GPQA | 4576.0 | 6.72 | 5.09 | 0.0 | 2.68 | 5.93 | 9.28 | 29.42 |
| MUSR Raw | 4576.0 | 0.41 | 0.05 | 0.29 | 0.37 | 0.41 | 0.44 | 0.6 |
| MUSR | 4576.0 | 9.98 | 5.84 | 0.0 | 5.09 | 10.02 | 13.61 | 38.69 |
| MMLU-PRO Raw | 4576.0 | 0.33 | 0.13 | 0.1 | 0.24 | 0.34 | 0.41 | 0.73 |
| MMLU-PRO | 4576.0 | 25.41 | 14.27 | 0.0 | 15.83 | 27.19 | 34.65 | 70.03 |
| Generation | 4576.0 | 0.76 | 0.8 | 0.0 | 0.0 | 1.0 | 1.0 | 10.0 |
相関分析
LLMの指標というのはたくさんあり、たとえばBBH(BIG-Bench-Hard)は多岐にわたる分野の「難しい(Hard)」タスクを集めたテストのスコアです。
で指標によっては似たような評価をしているものもありそうなので、相関係数行列を作ってみました。
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(10, 8))
evaluation_columns = [col for col in df.columns if 'Raw' in col or col in ['Average ⬆️', 'IFEval', 'BBH', 'MATH Lvl 5', 'GPQA', 'MUSR', 'MMLU-PRO']]
# Calculate the correlation matrix
correlation_matrix = df[evaluation_columns].corr()
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', fmt=".2f")
plt.title('Correlation Matrix of Evaluation Columns')
plt.savefig('correlation_matrix.png')
plt.savefig('correlation_matrix.svg')
plt.show()
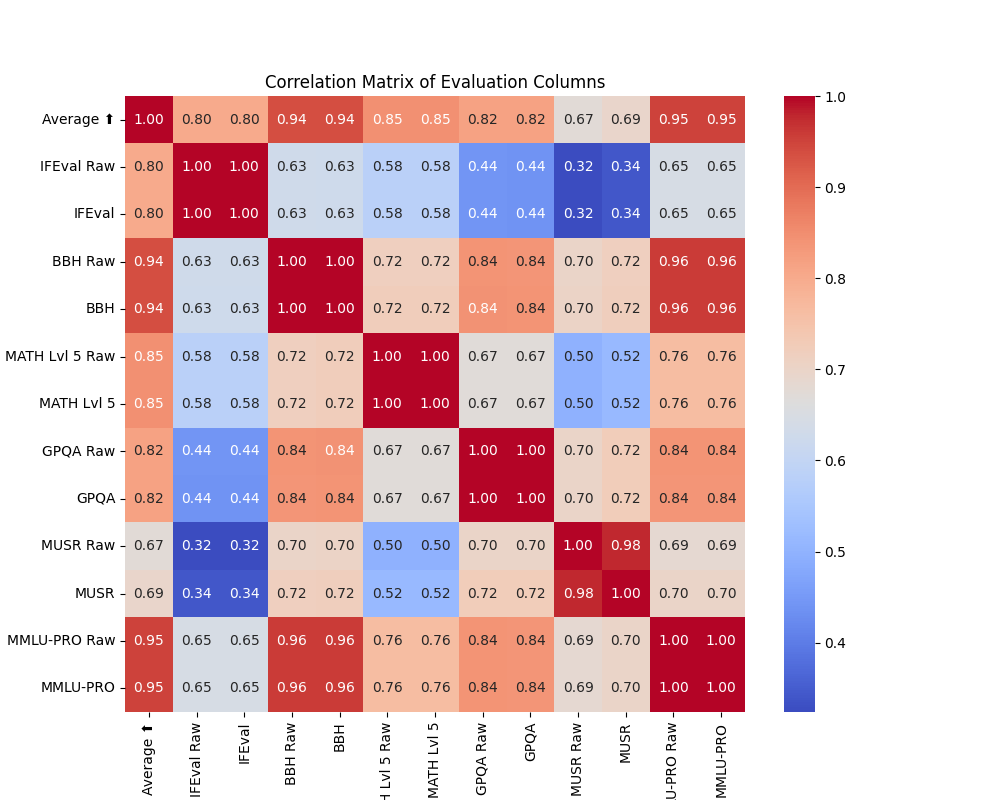
Averageは全体の平均値なので、全体と相関があるのは当たり前ですが、一番相関が低いペアはMUSRとIFEvalの0.32でした。
逆に近い指標がBBHとMMLU-PROで0.96でした。
Rawは元の値で足し算掛け算しただけなので相関値は同じです。たとえばBBHとBBH Rawは相関1ですよね。なのでこの二つの違いはここでは深く考えなくて良いです。
散布図
つまりはこの相関低ペアのMUSRとIFEvalの二つがLLMの異なる特性を測っている可能性が高いので、この二つで散布図をプロットしてみます。
全体の平均のカラムがあるのでこの平均Top10のもののみ名前を表記してみます。
import matplotlib.pyplot as plt
import numpy as np
# Sort by 'Average ⬆️' and get the top 10
top_10_df = df.nlargest(10, 'Average ⬆️')
plt.figure(figsize=(10, 8))
# Create scatter plot
plt.scatter(df['MUSR'], df['IFEval'], c=df['Average ⬆️']*10, alpha=0.5) # Size based on Average
# Add text labels for the top 10
for index, row in top_10_df.iterrows():
plt.text(row['MUSR'], row['IFEval'], row['eval_name'], fontsize=9)
plt.xlabel('MUSR')
plt.ylabel('IFEval')
plt.title('IFEval vs MUSR with Top 10 Average')
plt.grid(True)
plt.savefig('scatter_plot.png')
plt.savefig('scatter_plot.svg')
plt.show()
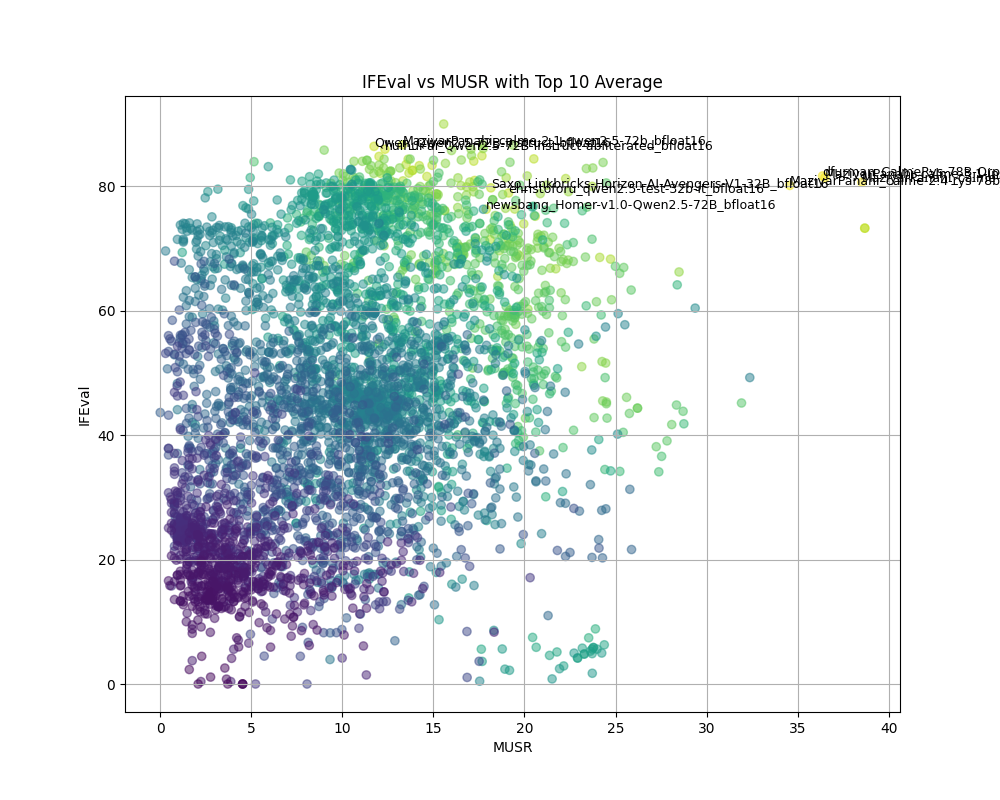
上の方を広げて表示
plt.figure(figsize=(14, 12))
# Create scatter plot
plt.scatter(df['MUSR'], df['IFEval'], c=df['Average ⬆️']*10, alpha=0.5) # Size based on Average
# Add text labels for the top 10
for index, row in top_10_df.iterrows():
plt.text(row['MUSR'], row['IFEval'], row['eval_name'], fontsize=9)
plt.xlim(20,40)
plt.ylim(50,100)
plt.xlabel('MUSR')
plt.ylabel('IFEval')
plt.title('IFEval vs MUSR with Top 10 Average')
plt.grid(True)
plt.savefig('scatter_plot_zoomed.png')
plt.savefig('scatter_plot_zoomed.svg')
plt.show()
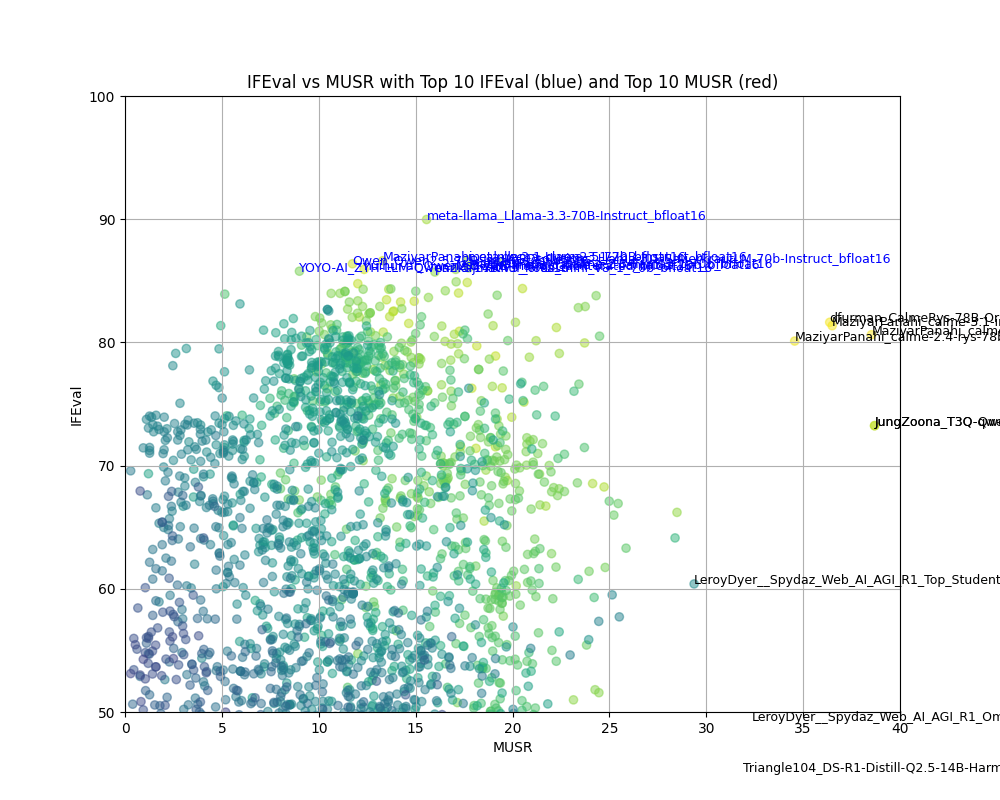
それぞれの軸のトップ10のモデル名を記入してみたんですが、重なって読めないので、ズームします。
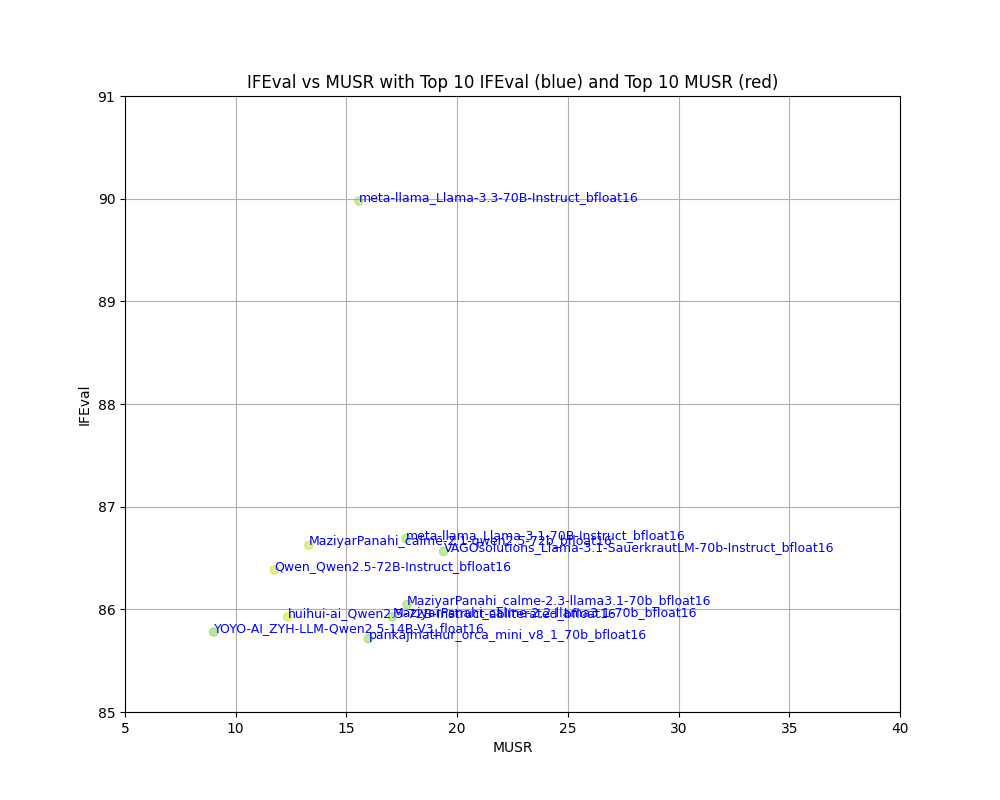
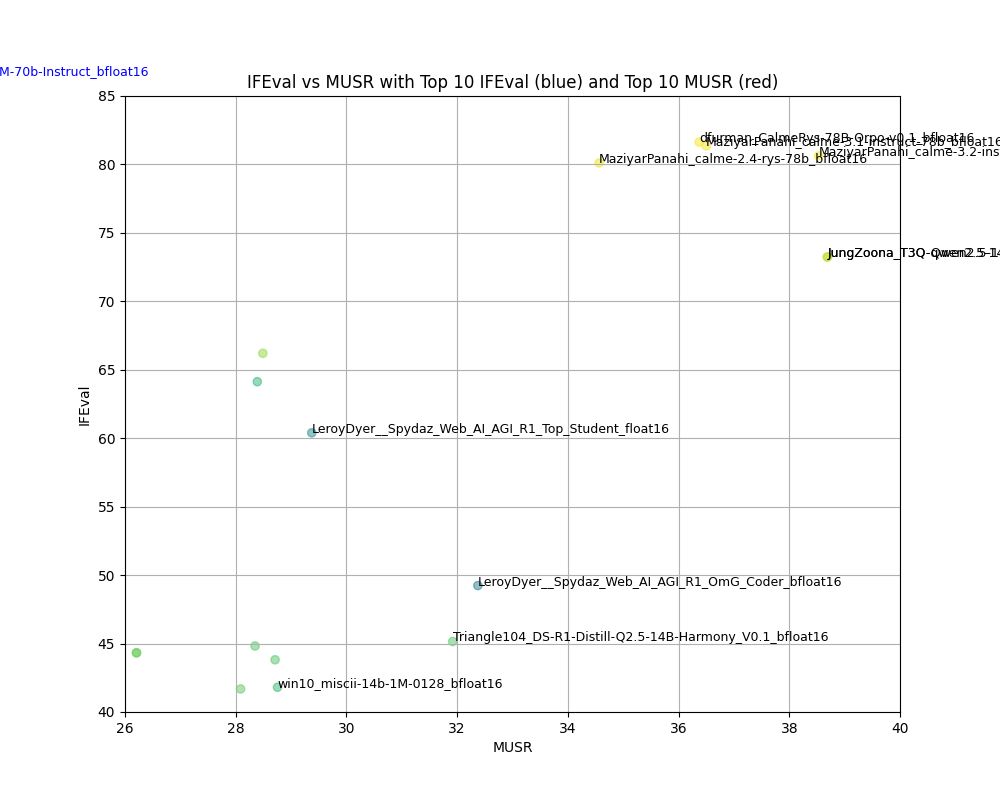
IFEvalの中にはllama-3.3-70Bとか、Llama-3.1-70B,qwen2.5-72B,calme-2.1といった文字が見えます。
MUSRのTOP10の中にはcalme-3.2-instruct-78b,calme-2.4-rys-78bとかqwen2.5-14bといった名前が見えます。
まだqwen3が出る前のためここにはないようです。
calmeというモデルは知りませんでした。
表は下の通りです。
IFEvalトップ10:
| eval_name | Precision | IFEval | MUSR | |
|---|---|---|---|---|
| 39 | meta-llama_Llama-3.3-70B-Instruct_bfloat16 | bfloat16 | 89.9758 | 15.5656 |
| 61 | meta-llama_Llama-3.1-70B-Instruct_bfloat16 | bfloat16 | 86.6885 | 17.6911 |
| 6 | MaziyarPanahi_calme-2.1-qwen2.5-72b_bfloat16 | bfloat16 | 86.6236 | 13.2971 |
| 60 | VAGOsolutions_Llama-3.1-SauerkrautLM-70b-Instruct_bfloat16 | bfloat16 | 86.5637 | 19.3854 |
| 5 | Qwen_Qwen2.5-72B-Instruct_bfloat16 | bfloat16 | 86.3838 | 11.7422 |
| 68 | MaziyarPanahi_calme-2.3-llama3.1-70b_bfloat16 | bfloat16 | 86.0466 | 17.7362 |
| 4 | huihui-ai_Qwen2.5-72B-Instruct-abliterated_bfloat16 | bfloat16 | 85.9267 | 12.3422 |
| 66 | MaziyarPanahi_calme-2.2-llama3.1-70b_bfloat16 | bfloat16 | 85.9267 | 17.0695 |
| 138 | YOYO-AI_ZYH-LLM-Qwen2.5-14B-V3_float16 | float16 | 85.7793 | 9.00286 |
| 70 | pankajmathur_orca_mini_v8_1_70b_bfloat16 | bfloat16 | 85.7143 | 15.9969 |
MUSRトップ10:
| eval_name | Precision | IFEval | MUSR | |
|---|---|---|---|---|
| 12 | JungZoona_T3Q-Qwen2.5-14B-Instruct-1M-e3_bfloat16 | bfloat16 | 73.2397 | 38.688 |
| 13 | JungZoona_T3Q-qwen2.5-14b-v1.0-e3_bfloat16 | bfloat16 | 73.2397 | 38.688 |
| 0 | MaziyarPanahi_calme-3.2-instruct-78b_bfloat16 | bfloat16 | 80.6261 | 38.5289 |
| 1 | MaziyarPanahi_calme-3.1-instruct-78b_bfloat16 | bfloat16 | 81.3555 | 36.4995 |
| 2 | dfurman_CalmeRys-78B-Orpo-v0.1_bfloat16 | bfloat16 | 81.6327 | 36.3721 |
| 3 | MaziyarPanahi_calme-2.4-rys-78b_bfloat16 | bfloat16 | 80.109 | 34.5661 |
| 2171 | LeroyDyer__Spydaz_Web_AI_AGI_R1_OmG_Coder_bfloat16 | bfloat16 | 49.237 | 32.374 |
| 379 | Triangle104_DS-R1-Distill-Q2.5-14B-Harmony_V0.1_bfloat16 | bfloat16 | 45.1504 | 31.9193 |
| 1592 | LeroyDyer__Spydaz_Web_AI_AGI_R1_Top_Student_float16 | float16 | 60.3953 | 29.374 |
| 613 | win10_miscii-14b-1M-0128_bfloat16 | bfloat16 | 41.8082 | 28.7547 |
リーダーボードの結果を主成分分析(PCA)で分析したという研究もありますので、興味があればそちらもどうぞ(Ruan et al.)。
Ruan et al. 2024
Ruan, Yangjun, Chris J. Maddison and Tatsunori B. Hashimoto. “Observational Scaling Laws and the Predictability of Language Model Performance.” ArXiv abs/2405.10938 (2024): n. pag.
Discussion