統計検定2級　アウトプット記述統計

目的

統計検定2級の映像授業と書籍内容を書き出す

記述統計

変数の分類

1. 質的変数
   • 名義尺度
     意味：同じ値かどうか
     例：性別、職業、出身地
   • 順序尺度
     意味：値の大小関係
     例：ランク評価、満足度
2. 量的変数
   • 間隔尺度
     意味：値の差の大きさ
     例：気温
   • 比例尺度
     意味：値の比
     例：長さ、重さ、価格

中心と散らばりの指標(量的変数)

1. 平均(中心指標)
   
   $$\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i$$

外れ値、データの偏りに注意

2. 分散・標準偏差(散らばり指標)

   • 分散
     

     $$s^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2$$

   • 標準偏差
     

     $$s = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2 }$$

標本分散・標本標準偏差の場合は分母が「$n-1$」になります。

3. 標準化得点（標準化指標）

   • 標準化：
     $$z = \frac{x - \bar{x}}{s}$$
     
     データの中心である平均を引くことで中心の値を０にし、ばらつきの値である分散を割ることでばらつき度合いを統一（標準偏差を１に）する。

4. 変動係数（標準化指標）

   • 変動係数：

     $$CV = \frac{s}{\bar{x}}$$
     
     標準偏差・分散は単位が違うと単純比較はできないが、平均で割ることで平均に対する散らばり具合に変換できる。

   • 目的：
     変動係数（CV）は、データのばらつきの大きさを「平均値に対する相対的な尺度」として比較したいときに使う。

順序統計量(量的変数)

分布の特徴を順位の視点で考える

1. 順序統計量

2. 箱ひげ図
   

箱ひげ図の構成要素:

• 箱:
  四分位数 (Q1, Q2, Q3) で構成され、データの中心部分を表します。
  Q1: データの小さい方から数えて25%の位置
  Q2: データの真ん中の値 (中央値)
  Q3: データの小さい方から数えて75%の位置
• ひげ:
  箱の両端から伸びる線で、データの最大値と最小値を表します。
• 外れ値:
  ひげの外側に個別でプロットされる、極端に大きいまたは小さい値。

箱ひげ図の活用:
データのばらつき具合の比較
外れ値の検出
分布の形状の把握 (左右対称、偏りなど)
複数のデータセットの比較

散布図と共分散(２つの量的変数)

２変数のばらつき方の'共鳴・シナジー'度合を指標化

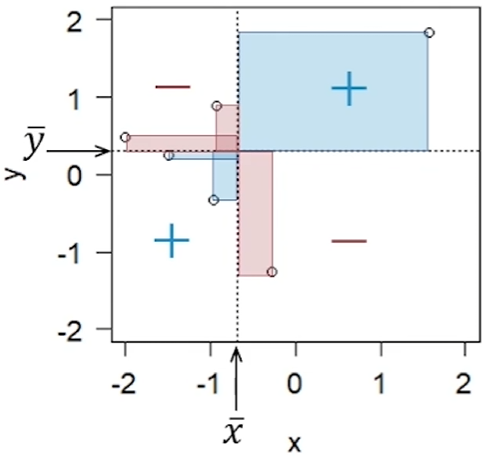
1. 共分散
   

   $$s_{xy} = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})$$

   ２つの分散の積、つまり散布図においての面積を求めている。面積の合計が０に近いほど２変数の共鳴度合いが低い。
   

2. 相関係数
   

   $$r = \frac{s_{xy}}{s_x s_y}$$

   共分散を２変数の標準偏差の積で割ることで、最小ー１，最大１に範囲を抑える効果がある。

3. 偏相関係数
   

   $$r_{xy\cdot z} = \frac{r_{xy} - r_{xz} r_{yz}}{\sqrt{(1 - r_{xz}^2)(1 - r_{yz}^2)}}$$
   
   

   • 見かけ上の相関（擬相関）の疑いがある場合はこれを使う。相関係数は因果関係を表すことができない。また、非線形な関係は表すことができない。

   • eg.）夏場の電力消費量が上がるほどアイスの消費量が上がる場合二つに因果関係があるように見えるが、実際には気温という３つ目の変数が二つに共通した因果関係のある変数である。

   • ３つ目の変数の影響を除く目的がある。

回帰直線

1. 回帰直線の式
   
   $$\hat{y} = a x + b$$

回帰ではこのa,bを如何にして求めるかがポイントである。
2. 残差と残差平方和

• 残差
  $$e_i = y_i - \hat{y}_i$$
  
  推測値である回帰直線の被説明変数と実際の数値の差
• 残差平方和
  $$RSS = \sum_{i=1}^{n} (y_i - \hat{y}i)^2 = \sum{i=1}^{n} e_i^2$$

これらは最小二乗法におけるa,bの推定に用いる。

3. 回帰係数と定数項
   

   $$b = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}$$
   $$a = \bar{y} - b \bar{x}$$

   回帰係数（傾き）$b$ の式
   

   $$b = \frac{\mathrm{Cov}(x, y)}{s_x^2}$$

   または、共分散と標準偏差を使って

   $$b = r_{xy} \frac{s_y}{s_x}$$

   $\mathrm{Cov}(x, y)$：xとyの共分散
   $s_x$：xの標準偏差
   $s_y$：yの標準偏差
   $r_{xy}$：xとyの相関係数
   $x_i, y_i$：各データの値
   $\bar{x}, \bar{y}$：それぞれの平均値
   $n$：データの個数
   $b$：回帰係数（傾き）
   $a$：定数項（切片）

4. 決定係数
   

   $$R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}i)^2}{\sum{i=1}^{n} (y_i - \bar{y})^2}$$

   $R^2$：決定係数
   $y_i$：実測値
   $\hat{y}_i$：予測値（回帰直線上の値）
   $\bar{y}$：目的変数$y$の平均値
   $n$：データの個数

   $$R^2 = 1 - \frac{S_r}{S_y}$$

   $S_y = \sum_{i=1}^{n} (y_i - \bar{y})^2$：全変動（総平方和, Total Sum of Squares）
   $S_r = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$：残差平方和（Residual Sum of Squares）
   $y_i$：実測値
   $\hat{y}_i$：予測値（回帰直線上の値）
   $\bar{y}$：目的変数$y$の平均値
   $n$：データの個数

時系列データ

項目	数式例	解説
差	$y_{t+1} - y_t$	連続する時点での変化量（増加または減少の絶対量）
変化率	$\frac{y_{t+1} - y_t}{y_t}$	時点$t$から$t+1$への相対的な増減率。成長率などで使われる。
幾何平均（T期間）	$y_T = y_0 \times r_G^T$ $r_G = \left( \frac{y_T}{y_0} \right)^{1/T}$	期間全体の平均成長率を求める。経済成長などの長期変化の分析に用いられる。
指数化（S時点基準）	$q_t = \frac{y_t}{y_S}$	時点$S$を基準として、各時点の値を相対的に表現する。ラスポイレス指数などに応用。

正直幾何平均よくわからないのでAIに聞いてみた

① 幾何平均（T期間）
どんなもの？
ある期間（たとえば5年など）にわたって、データがどれくらいのペースで増えたか（または減ったか）を、毎年一定の割合だったと仮定して計算する方法です。

なぜ使うの？
毎年バラバラに変動していても、全体として「毎年○％くらいずつ増えた」とか「減った」とざっくり理解したいときに便利です。

具体例
たとえば、ある会社の売上が

1年目：100

5年目：200

になったとします。
このとき「5年間で毎年どれくらいずつ成長した？」を求めるのが幾何平均です。
結果は「毎年約14.9%成長した」となります（この計算には累乗やルートを使います）。

② 指数化（S時点基準）
どんなもの？
ある基準の年（たとえば2020年）を「1」と決めて、他の年の値がどれくらい増えたり減ったりしているかを、比で表す方法です。

なぜ使うの？
グラフでの比較がしやすくなり、数字の絶対的な大きさに関係なく「どれくらい増えた？」「減った？」がパッと分かります。

具体例
2020年の物価を「1」としたとき、

2022年の物価が2020年の1.1倍なら → 2022年の指数は「1.1」

2019年の物価が2020年の0.9倍なら → 2019年の指数は「0.9」

つまり「2020年と比べてどうなのか？」が分かるようになります。

どちらも、時系列データ（時間によって変化するデータ）を「分かりやすく」「比較しやすく」するためのテクニックです。

おわりに

基本的な高校レベルの統計でも、使っていないとこんなにも忘れているのかと驚きました。大体理解できましたが、時系列データの理解がまだ甘いので書籍を読み込もうと思います。

参考書籍：入門統計解析法 永田靖