【コード全公開】物理をグラフィカルに学習・教育するための物理シミュレータの紹介と使い方
1. 概要
本文書では、自作の物理シミュレータを用いて運動方程式のシミュレーションを行う方法を解説します(以下のYouTubeの動画のようなシミュレーションが出来るようになります)。
コードは全公開しているため、自由に改変していただきご自身の活動に役立ててほしいと思っております。
私自身、高校で物理を学び、大学・大学院では人工衛星のシミュレーションに取り組んできました。振り返ると、もう8年以上物理に触れてきており、見慣れた運動方程式であれば挙動を頭の中で予測できるようになってきました。
そんな経験の中、以下のような問題があるように感じてきました。
- 運動方程式を見ても物体がどんな動きをしているのか頭の中で分からない
- 教科書には運動方程式を解いた結果としてグラフしか示されていない
- グラフィカルに物理のシミュレーションを行った動画は少ないし、個人利用してよいか迷う
- 物理を教えるためのグラフィカルに物理シミュレーションをする方法がない
- 物理エンジンにお金を出せない(または物理シミュレータを委託するほど学校にお金がない)
2. はじめに
2.1. 対象読者
本文書の対象読者としては、以下を想定ししております。
- 物理を教える際に物体の動きをグラフィカルに見せたい高校教師
- 大学での物理や工学で、運動方程式の理解を深めたい大学生・大学院生
- (物理をわかりやすく教えたい大学教員)
- 視覚化に興味があるプログラミング初学者やエンジニア
2.2. 目的
本文書の目的は、「対象読者が自由に物理シミュレーションを行える環境を与える」ことです。
そのために、可能な限りコードもシンプルに書いています。
2.4. 仮定 / 環境
特に固有の環境は必要ないです。私は以下の環境を用いております。
- windows11 / macbook air
- Python 3.10.6
- processing 4.3
- VSCode(コードは用意しているので編集時はメモ帳で構いません)
- GitHub(コード格納場所)
今回はこれらの環境のインストール方法は参考文書を示すことに留めたいと思います。
学校でも使える環境を想定してこのようにしています。
(unityを使えばよい気もしますが、学習コストと必要なスペックがそれなりに高いので)
2.5. 略語 / 用語
- 物理シミュレータ:物理現象をコンピュータ上でシミュレーションするためのソフトウェア
- グラフィカル:2Dや3Dで視覚的に分かり易いということ(数値のみではない)
- python:簡単に書けるプログラミング言語、今回は演算を担当
- processing:アニメーションを簡単に作れるプログラミング言語、今回はグラフィカルに表示する担当
- GitHub:コードを格納しているwebサイト、ソフトウェア開発にはほぼ必須
3. 環境設定
3.1. インストール
本文書で紹介するコードを動かすためには、Python環境の準備と、Processingとの通信を行うための設定が必要です。PythonとProcessingの基本的なインストール方法については、それぞれのPythn japanのサイトおよびProcessing公式サイトのドキュメントをご参照ください。
サイトの通りに進める(基本的にはwindowsならxxx.exeをダブルクリックして出てくる画面に従う)ことでインストール可能ですが、大体上手くいかないときの原因は以下なので困ったら以下のキーワードでトラブルシューティングしてみてください。
- 環境変数の設定(PCのどこからでもpythonやprocessingを使うためには、インストールされたフォルダの場所を環境変数に登録してオープンにする必要があります)
- (Windowsの場合)Microsoft Store版のpythonを使うように誘導されStore経由でインストールさせられている→アンインストールしてサイトの通り行う
環境設定で詰まり、調べても分からず、この記事の先に進めない場合は本記事にコメントください。
3.2. 必要なPythonライブラリのインストール
Pythonでシミュレーションを行うために、いくつかのライブラリが必要です。コマンドプロンプトやpowershell、terminal等を開き、以下のコマンドを使用して必要なライブラリをインストールしてください。
pip install numpy matplotlib
- numpy:数値計算を行うためのライブラリです。物体の位置・速度ベクトルや力の計算に使用します。
- matplotlib:データを可視化するためのライブラリで、シミュレーション結果のプロットに使用します。
デフォルトのPythonインストールにはソケット通信用のライブラリsocketが含まれていますので、追加インストールは不要
3.3. ソケット通信に関する設定
本節の設定は、別途特殊な設定をされている方向けです。
ソケット通信を行うには、ホストとポートの設定が必要です。この記事でのサンプルコードでは以下の設定を使用しますが、特に変更が必要な場合はご自身の環境に合わせて適宜調整してください。
- ホスト: 127.0.0.1(ローカルホストを指定します。PythonとProcessingが同じPC上で動作する前提です。)
- ポート番号: 10001(未使用のポートであることを確認し、他のソフトウェアと競合しないように設定してください。)
3.4. 今回使うプログラムのダウンロード
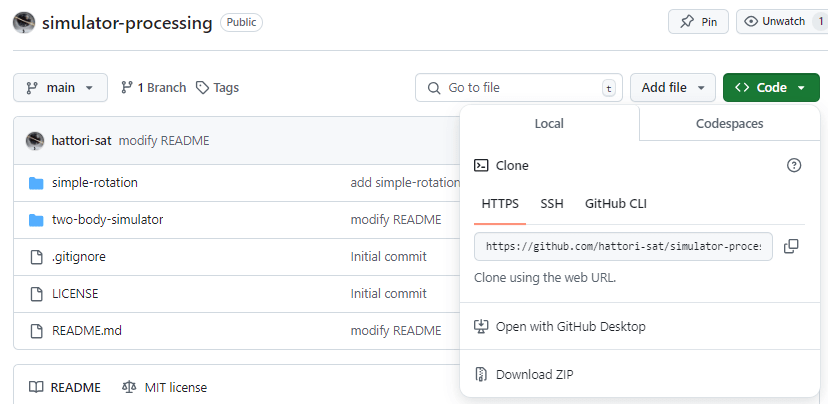
本文書のために作成したコードは以下のGitHubに格納しています。
ダウンロードする方法は二つあります。
-
git clone https://github.com/hattori-sat/simulator-processing.gitをターミナルで実行 - リンク先で
Codeボタンを押下し、Download ZIPを押下
4. シンプルなプログラムの実践
ここから本題に入ります。
まずは、以下の動画のように立方体を回転させてみましょう。
4.1. プログラムのデモ
3.4節の方法でダウンロードした結果、以下のようなフォルダ構成になっていると思います。
どこでもzipを解凍した場所(自分はDownloadsに解凍しました)
├─simulator-processing
│ ├─simple-rotation
│ │ └─rotation3DServer
│ └─two-body-simulator
│ └─twoBodySimulator
今回は、とりあえずDownloadsフォルダにzipを回答した上記のフォルダ群があるものとして話を進めていきます。(どこにフォルダをおいても動作はしますが、cdなどのコマンドの操作に慣れていない場合は同じ状況で動作させることをお勧めします。)
ここでは、simple-rotationのフォルダの中身を使っていきたいと思います。
以下の4つのフローで実行していきましょう。
-
rotation3DServerの中に入っているファイルをダブルクリック - Fig. 4.1-1の画面が開くので、左上の
▶ボタンを押下 - この状態でPowershellを立ち上げる
-
rotation_client.pyを実行するために、以下のようにpowershellでコマンドを打つ(任意の方法で問題ないです)。
PS C:\Users\hatto> cd .\Downloads\
PS C:\Users\hatto\Downloads> cd .\simulator-processing-main\
PS C:\Users\hatto\Downloads\simulator-processing-main> cd .\simulator-processing-main\
PS C:\Users\hatto\Downloads\simulator-processing-main\simulator-processing-main> cd .\simple-rotation\
PS C:\Users\hatto\Downloads\simulator-processing-main\simulator-processing-main\simple-rotation> python .\rotation_client.py
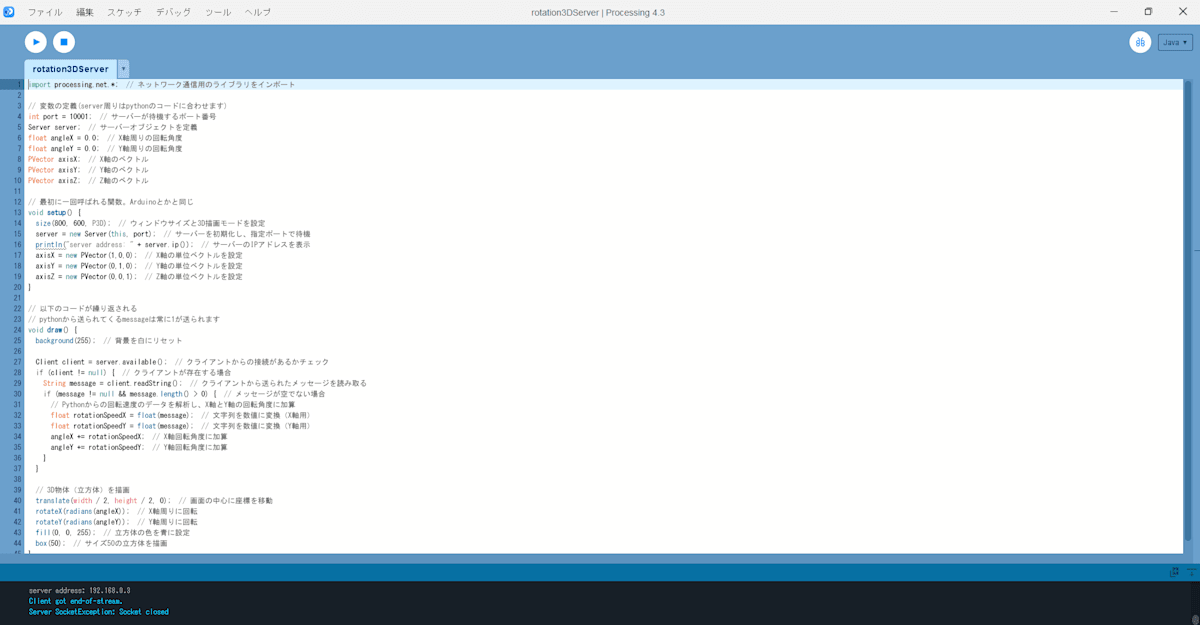
Fig.4.1-1 rotation3DServer.pdeを開いた結果
4.2. プログラムの説明
ここでは簡単に説明をしていきたいと思います。
全体の説明は今回は省略したいと思います。
今回作成したプログラムは以下のような構成になっています。

Fig. 4.2-1 processingとpythonの役割
4.2.1. processing
コードの全体は以下のようになっています。(//のある行はコメントアウトと呼ばれ、プログラムには影響を与えないメモです。)
processingでは起動時に setup() 関数を実行します。
ここでは以下のことを行っています。
- processingによって開く画面のウィンドウサイズの設定
- pythonとの通信を行うserverの設定
その後に、draw() 関数をループします(何回も実行します)。
*draw()*関数の中でも以下の部分では、クライアント(今回はpythonのプログラム)からの接続があるかをチェックして、接続があればpythonから送られてきた文字列を読み取り、rotationSpeedXとrotationSpeedXに保存しています。
4章のプログラムで理解していただきたいのは以下の点です。
- socket通信と呼ばれる通信でpythonと通信している
- socket通信で送られてくる文字列を上手く変換してprocessingの変数に代入する
4.2.2. python
コード全体は以下のようになっています。(#のある行はコメントアウトと呼ばれ、プログラムには影響を与えないメモです。)
以下のコードで、socket通信を行うための設定をしています。
4.2.1.項にてprocessingではpythonからの文字列を受け取っているということを説明しました。以下のコードがpythonからprocessingに文字列を送っている部分です。ここでは、1という文字が格納されているmessageを送っています。
socket通信なるものをしているとなんとなく理解していただければ、socket通信周りのコードを本文書では追う必要はありません。
4.2.3. プログラムがなぜ分けられているのか
さて、もしかしたら本文書を読んでる方の中にはなぜこんな長いコードを書くのだろうかと思った方もいるかもしれません。
確かにこのコードは単純にx軸とy軸周りに1 radの回転を与えているだけです。processingだけでも書けます。
コードが長くかつ2つのプログラムに分けられているのは、以下のような理由がありますので、4章ではこれらのことを学んでいただけていると次の章に進みやすくなります。
メリット(プログラミングをよく学びたい人向け)
-
責務の分離によるコードの明確化
- Pythonは、物理シミュレーションの計算やサーバーとしての役割に特化しています。数値計算やデータの生成など、演算が中心の処理に向いているPythonの特徴を活かして、物体の動きや状態のシミュレーションを担当させています。
- Processingは、ビジュアル表現に特化しています。Pythonから送信されたデータを受け取り、物体の軌跡や動きをグラフィカルに表示します。Processingの特徴である直感的なグラフィック処理を活かし、データの視覚化を担う役割として位置づけられています。
-
モジュール性の向上
PythonとProcessingを分けることで、それぞれのモジュール性が高まります。以下のメリットがあります。- Python側のシミュレーションコードを変更しても、Processing側の描画コードへの影響が最小限に抑えられるため、修正が容易になります。
- Processing側の表示の詳細(色、形状、表示方法)を自由にカスタマイズでき、Python側のシミュレーションロジックを維持したまま、可視化の変更が可能です。
-
性能と開発効率の最適化
PythonとProcessingを分けた構成により、各環境で得意な部分を活かした処理性能の最適化が可能になります。- Pythonがシミュレーション計算の負荷を持つことで、効率的な演算が行える一方、Python単体では得にくいグラフィック表示をProcessingが補います。
- Processingが描画処理を担うため、計算負荷を軽減しながらリアルタイム性のあるビジュアライゼーションを実現しています。
- 学習と拡張の容易さ
PythonとProcessingに分けることで、今後それぞれの環境に特化したライブラリや技術を学び、適用しやすくなります。例えば:- Pythonで新しい物理シミュレーションモデルやデータ構造、さらには他の計算ライブラリを組み込むなど、計算能力を向上させる方法を自由に追求できます。
- Processingで新たなビジュアライゼーション手法やアニメーションの技術、あるいはユーザーインターフェースの改良に挑戦する余地が生まれます。
- マルチプラットフォーム対応
今回の分離により、異なるプラットフォームでの動作や、ネットワーク越しのデータ送信なども容易になります。将来的に、異なるデバイス上で計算と表示を分担させるような、ネットワーク処理を伴う拡張もスムーズに行えます。
5. 2つの物体の物理シミュレーション
さて、この5章が本文書の目玉となります。
以下の物理シミュレーションをすることが目的となります。
5.1. 今回の物理モデル
今回使用する物理モデルは、高校物理でよく見るモデルとなります。

*Fig. 5.1-1 2物体間には摩擦があり、床とは摩擦がない物理モデル
このモデルは非常に基礎的なのですが、多くの高校生たちを最初に悩ませていることでしょう。
なぜならば、
- 2つの物体の相対速度を考えなければならない
- 摩擦によって2物体が同じになっても全体としては進行している
- 「止まっている」のか「止まっていない」のか想像できない
5.2. 運動方程式
Fig. 5.1-1に示したモデルでは、
また、直交座標系を定義し、地面に対して平行に
このとき、
さて、これらの仮定を置くことで、以下のような運動方程式を立てることが出来る。(なお、
加速度やその他についての補足
読者の中には、
今回の物理モデルでは、座標系が静止もしくは等速直線運動をしている慣性系なためいずれの座標系においても上の式は成りたちます。
そのほかにもモデルが剛体として書かれているのが気になる方もいるかもしれません。
今回は密度が一様に分布している物体を考えて、重心の運動方程式を考えていると考えてください。
5.3. 高校物理での解き方
式(1)と式(2)を見ると
ここでは公式の説明は省くことにするが、要は
- 速度が線形的に変化する
- ゆくゆくは2つの物体の速度は同じになる(相対速度は0になる)
- (2物体を一つの物体とみなすと摩擦力は内力になるので運動量保存が成り立つので2つの物体が同じ速度になったときは以下の式の速度
v_{f}
5.4. プログラムの説明
実行手順は4.1.節と同じ流れで実行できます。
downloadしたフォルダの中のtwo-body-simulatorに入っています。
5.4.1. python
さて、先ほどとは順番を変えてpythonから説明をします。
基本的には運動方程式を数値的に解く(数値積分する)クラス SimulatorObjectを使います。
このプログラムを使うためには、オブジェクト指向についての簡単な理解が必要です。
classというのは、シミュレーションに使う変数や(プログラムの)関数をまとめたツールキットのようなものです。
以下の部分がclassの定義です。(今追う必要はありません)
以下のメソッドinitはクラスを使うときに最初に呼ばれます。今回は特に何も変更する必要はありません。
しかし、ほかの運動方程式をシミュレーションしたい場合は、必要なパラメータをここで定義しましょう。例えば、ばね定数が必要であれば、self.k = 1のように加えてみましょう。
rk4については省略します
その下のメソッド*rk4()*は数値積分をルンゲクッタ法で行う部分です。
式(1)と式(2)をみると、運動方程式は2階の微分方程式であることが分かると思います。
要は2回積分すれば、位置の関数(
さて、一番重要な運動方程式をプログラムに入れている部分を説明します。
この部分では、加速度イコールの式の形でコードを書いています。(つまり、式(1)は
そして、以下のコードはパラメータを設定するために使います。これはmainの部分を見れば使い方が分かると思います。
mainの部分に入る前にsend_position_dataについて見ましょう。
ここで4章で説明したように文字列のmessageを送る機能を実装しています。
f-Stringを用いて値を
さて、mainの説明に入ります。
まずは初期値の設定を行います。運動方程式を解くためには初期値を決める必要があります。
次に初期値をclass(インスタンス)にセットします。
これによって、初期値が反映されます。
外力(摩擦力の設定はループの中で行います)の設定は、以下のようにしています。2つの物体の相対速度が0になったら摩擦力は発生しないため、このように条件分岐をしています。
ちなみに-np.array(external_force)としているのは、本当は-external_forceとしたいところですがlistにはそのような機能はないため、このようにしています。
あとは適当な時間間隔でデータをprocessingに送信しています。
5.4.2. processing
基本的にはこちらのコードは変更する必要はありません。そのため、ブラックボックスとして利用することが可能かつコメントアウトで変更点は大体わかると思いますので割愛したいと思います。
ここでは、pushMatrixとpopMatrixについて説明したいと思います。
該当部は以下のコードとなります。
口で説明するより図で説明した方が早いと思いますので、Fig.5.4-1に示します。

fig.5.4-1 pushMatrixとpopMatrix
5.5. 使い方のデモ
今回のデモでは2つの例を示したいと思います。
5.5.1. 物体の上で物体が静止する例
提供した以下のGitHubの例では以下の初期条件を設定しています。(初期条件はpythonで設定しています。)
摩擦力は、
このときのシミュレーション結果が以下の通りです。
若干動画を撮影している関係で処理が重たくなっていますが、左上のPositionやVelocityの値をみると後半はObject1とObject2の速度が一致してその後一緒に動いていることが分かります。
また、2つの物体が同じになったときの速度についても注目していただきたく、式(4)に今回の初期値を代入してみると、最終的に速度が同じになったときの速度は、
となり、シミュレーション結果と一致しています。
また、実はこのpythonプログラムではグラフも自動で書いて保存してくれます。以下のようなグラフを書いてくれます。

Fig.5.5-1 Object1の位置の時間履歴

Fig.5.5-2 Object1の速度の時間履歴
Fig.5.2-2 から速度が変化しなくなった(摩擦力を受けなくなった)のは25秒程度であることが分かります。
これは今回の例を式に当てはめてみると分かります。
このように理論的に解いた結果とシミュレーション結果がほとんど同じになっていることが確認できます。
これだけでも物理に対する理解が深まると思っているのですが、2つ目の例をみてさらにこのシミュレーションの結果から推察を得ることが出来ることを期待しています。
5.5.2. 物体の上で物体が静止しない例
さて、初期値を変えて色々試してみることが物理を理解するうえで重要だと考えています。
例えば、Object1の初期速度をもっと早くしてみたらどうなるでしょうか。初期値を以下のように変更してみましょう。
プログラムで言うと以下の部分をobject1_init_vel = [14, 0] # (Vx, Vy) [m/s]と変更すればよいです。
すると以下の動画のようなシミュレーション結果となりました。
動画の結果、Object1(青色)はObject2(赤色)の上にはなくなっていますが、宙に浮きながらも摩擦を受けているような挙動をしています。
この状況は正しいでしょうか?
現実世界ではありえませんね。しかし、物理シミュレーションではありえます。
理由としては以下の2つのどちらかです。
- 物理モデルが不十分(Object1がObject2からはみ出たときのモデルを定義していない)
- processingが表示している四角形が問題より短い
1つ目の理由は分かり易いと思います。なぜなら、今回は式(1)から式(3)の運動方程式しかシミュレーションしていないので、「回転」や「物体から落下」という動きはモデルに入れていないのです。(余談ですが、物理エンジンはこの辺りの運動方程式をたくさん実装して出来ています。)
2つ目の理由は以下のコードのことを言っています。ここで四角形の幅は100[m]、高さは50[m]としています。(現実で考えるとかなり大きいです)
この幅が十分に大きい(つまり、Object1がどんなスピードであったとしても落ちない大きさ)であればよかったという考え方もできます。
高校物理などでは落ちないためにはObject2(物体2)の幅(長さ)はどの程度必要であるかという問題も出てくると思います。
上記のような動画を見れば、「落ちる」という状況がどういうことなのか一目瞭然だと思います。
5.5.3. さらに発展すると
初期値によって挙動が大きく変わる物理モデルというのはたくさんあります。
たとえば、Hillの方程式という衛星の挙動を表す運動方程式があります。
以下のシミュレーションゲームでは、宇宙での衛星の挙動を表す運動方程式をシミュレーションして球を動かしています。打ち出す位置によって動きが変わっていることが分かると思います。
このようにprocessing内に画像を取り込んでゲーム風に見せることも可能です。
画像を取り込むなどの説明は今回は割愛させていただきますが、このように大学生も物理シミュレータを用いて理解を深めることが出来ると思います。
6. 本シミュレータの活用手段
本シミュレータは、windows PCやmacbook airでも動作可能です。
pythonは現在教育でも使われているようなツールですし、processingもそんなにインストールに手間がかかるものではありません。
可能であれば、手元のPCに入れていつでもシミュレーションができる環境にあることが望ましいと考えています。
その上でプログラムのどこを変更するべきなのかをこの章でまとめておきたいと思います。
■初期値を変更
■運動方程式に使うパラメータを追加(massなどに合わせて作成しましょう)
■運動方程式を以下に記載します。
■パラメータを設定するためのメソッドを定義しましょう。
■上記で定義したメソッドを用いて、どんな条件でパラメータがどんな値を取るかを考えましょう。
■processingで表示する四角形の大きさなどを以下を変えて調整しましょう。
7. おわりに
本文書及び提供するコード自体が学習コンテンツとして利用できるようなものとなっていれば幸いです。
また、今回のコードではMITライセンスを付与しています。よく分からないと思いますので簡単に説明をすると、以下のようなものです。
- 私が書いたコードには著作権が自動的に発生します
- 著作権がある場合は誰かがそのコードを使用、改変、再配布するには、著作権者の許可が必要
- しかし、MITライセンスを付与すれば「著作権表示をすれば自由に使っていい」と示せます
- それにより、著作権表示があれば利用者は安心して使用や改変、再配布ができます
プログラムを読んで気づいた方もいるかもしれませんが、np.matrixで初期値などを定義しています。
これは大学生になると行列形式でプログラムを書くことが多くなるためです。
このようにこのプログラムでは拡張性を持たせております。
この題材を用いて、固有値を説明した文書を有料で公開しようと思いますのでお待ちください。
ここまでお読みいただきありがとうございました。
この文書がお役に立つことを祈っております。
ご指摘の点や修正する点などございましたら、気軽にコメントいただけますと幸いです。
また、GitHubに対しても気軽にforkしていただいたり、PRを出していただけますと幸いです。
もし、コメント等をしにくい場合は、hattori.sat@gmail.comまでご連絡ください。
8. 参考文献
- 高校物理ICT教材、https://physics.cloudfree.jp/
GitHub:
テンプレート:
Discussion
本文書を元にYouTubeの動画を作成しました。
お時間あればご覧ください。