📓
ALDS1(01~06)をRustで解説してみた
はじめに
この記事は AOJ(Aizu Online Judge) の ALDS1(Algorithms and Data Structures I) をRustで実装したものの解説記事です。
GitHubの alds1-rust リポジトリに、各問題ごとのRustによる実装例を掲載しています。
詳細は README.md をご覧ください。
問題の解説
ALDS1-01
A. 挿入ソート <Problem Link>
以下のsort関数は要素を1つ取り出し、その要素を正しい位置に挿入するソートの過程を出力しています。
挿入ソートとは
挿入ソートは、要素を1つずつ取り出して、すでにソートされた部分の適切な位置に挿入してソートするアルゴリズムです。
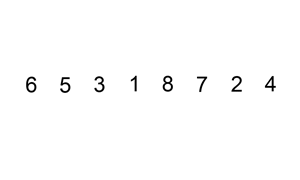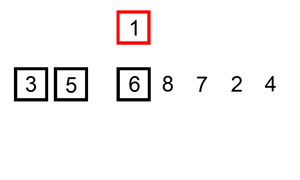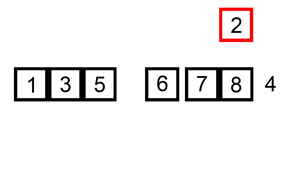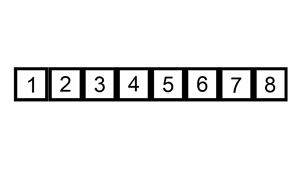
出典: Wikipedia 挿入ソート
alds1_01_A.rs
/* num: 要素の数, data: 入力された数列 */
fn sort(num: usize, mut data: Vec<u64>) {
let mut v: u64 = 0;
let mut j: usize = 0;
for i in 1..num {
v = data[i]; // 要素を1つ取り出す
j = i;
while j>0 && data[j-1]>v { // jが正の整数かつdata[j-1]がvより大きい場合
data[j] = data[j-1]; // data[j-1]の要素をdata[j]にずらす
j = j-1;
}
data[j] = v; // vを正しい位置に挿入
for i in 0..num {
print!("{}", data[i]); // ベクタの要素を出力
if i != num-1 {
print!(" ");
}
}
println!("");
}
}
B. 最大公約数 <Problem Link>
以下のgcd関数はユークリッドの互除法を用いてxとyの最大公約数を効率的に求めています。
alds1_01_B.rs
/* x: 入力された整数, y: 入力された整数 */
fn gcd(mut x: u64, mut y: u64) {
if x<y { // x > y になるようにする
let buf = x;
x = y;
y = buf;
}
while y>0 { // ユークリッドの互除法を用いる
let r = x%y; // rにxをyで割ったときの余りを代入
x = y; // xにyを代入
y = r; // yにrを代入（yが0になるまでループ）
}
println!("{}",x); // 最大公約数を出力
}
参考資料：https://ja.wikipedia.org/wiki/ユークリッドの互除法
C. 素数 <Problem Link>
以下のisPrime関数は試し割り法を用いてxが素数かどうかを判定します。
試し割り法とは
試し割り法は、ある数が素数かどうかを判定するために、その数の平方根までの整数で割り切れるかどうかを調べるアルゴリズムです。
- 例: 103 の場合
103 = a × b (a ≤ b)とします。
このときaを 2、3、...、103と順番に割っていきますが、
a = 11のとき、b = 9.36...となり、a ≤ bの条件を満たさなくなります。
つまり、aが平方根より大きい場合、bは平方根より小さくなるため、bはすでに調べた数の中に含まれていることになります。
よって、その数の平方根までの整数で割り切れるかどうかを確認すれば十分なので、
√103 ≒ 10.14なので、2、3、...、10までを調べればよいことになります。
alds1_01_C.rs
/* x: 入力された整数 */
fn isPrime(x: u64) -> bool {
if x==2 { // xが2の場合が素数なのでtrueを返す
return true;
}
else if x<2 || x%2==0 { // xが2未満、2の倍数の場合はfalseを返す
return false;
}
let limit: u64 = (x as f64).sqrt() as u64 + 1; // limitを(xの平方根)+1とする
let mut i = 3;
while i<=limit {
if x%i==0 { // xがiで割り切れた場合はfalseを返す
return false;
}
i += 2; // 偶数の場合は考慮しないので2ずつ加算する
}
true // 上記以外の場合は素数なのでtrueを返す
}
D. 最大の利益 <Problem Link>
以下のmax_prof関数はこれまでに出現した最小値(最安値)を記録しながら、各時点で「現在値 - 最安値」の差(利益)が最大になるように更新していきます。
alds1_01_D.rs
/* data: 時刻tにおける価格, num: 要素の数 */
fn max_prof(data: Vec<u64>, num: usize) -> i64 {
let mut minv: i64 = data[0] as i64; // 最小値
let mut maxv: i64 = (data[1]-data[0]) as i64; // 最大利益
for i in 1..num {
let j: i64 = data[i] as i64; // 要素を1つ取り出す
if maxv<j-minv { // j-minvが最大利益より大きい場合
maxv = j-minv; // j-minvをmaxvに代入し最大利益を更新
}
if j<minv { // jがminvより小さい場合
minv = j; // jをminvに代入し最小値を更新
}
}
maxv // maxv(最大利益)を返す
}
ALDS1-02
A. バブルソート <Problem Link>
以下のbubbleSort関数はバブルソートアルゴリズムを用いて、dataを昇順にソートします。
バブルソートとは
バブルソートは、隣り合う要素の大小比較と並べ替えを繰り返して、全体をソートするアルゴリズムです。
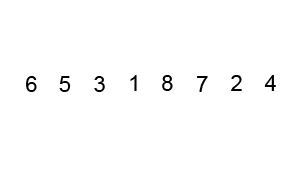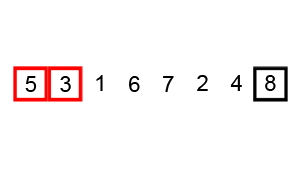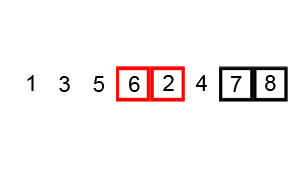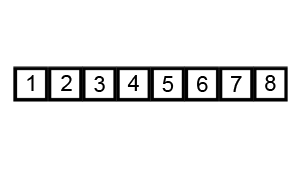
出典：Wikipedia バブルソート
alds1_02_A.rs
/* num: 要素の数, data: 入力された数列 */
fn bubbleSort(num: usize, mut data: Vec<u64>) {
let mut flag: bool = true;
let mut count: usize = 0;
while flag {
flag = false;
for i in (1..num).rev() {
if data[i]<data[i-1] { // data[i]がdata[i-1]より小さい場合
let tmp: u64 = data[i]; // 一時的にdata[i]をtmpに保存
data[i] = data[i-1]; // data[i-1]をdata[i]に移動
data[i-1] = tmp; // tmpの値をdata[i-1]に移動
flag = true;
count += 1; // 交換回数をカウント
}
}
} // dataがソートされている場合、flagはfalseのままなのでwhileループを抜ける
print(data); // print関数でソートされたdataを出力
println!("\n{}",count); // 交換回数を出力
}
B. 選択ソート <Problem Link>
以下のselectionSort関数は選択ソートアルゴリズムを用いて、dataを昇順にソートします。
選択ソートとは
数列の中から最小（または最大）の要素を選択し、先頭の要素と交換する操作を繰り返してソートするアルゴリズムです。
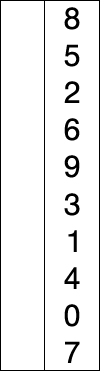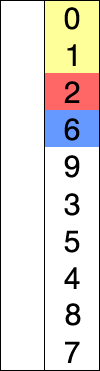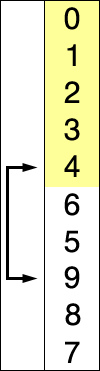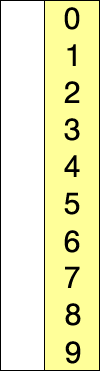
出典: Wikipedia 選択ソート
alds1_02_B.rs
/* num: 要素の数, data: 入力された数列 */
fn selectionSort(num: usize, mut data: Vec<u64>) {
let mut count: usize = 0;
for i in 0..num {
let mut minj: usize = i;
for j in i..num {
if data[j]<data[minj] { // data[j]がdata[minj]より小さい場合
minj = j; // jをminjに代入し、最小値のインデックスを更新
}
}
if i!=minj { // iとminjが異なる場合
let tmp: u64 = data[i]; // 一時的にdata[i]をtmpに保存
data[i] = data[minj]; // data[minj]をdata[i]に移動
data[minj] = tmp; // tmpの値をdata[minj]に移動
count += 1; // 交換回数をカウント
}
}
print(data); // print関数でソートされたdataを出力
println!("\n{}",count); // 交換回数を出力
}
C. 安定なソート <Problem Link>
以下の関数はバブルソートと選択ソートを用いてdataを数字の昇順にソートします。
※同じ数字が複数ある場合は入力された順番を保ちます。
data(入力されたカードの情報)の型について
- dataはタプルの
Vec<(char, u64)>で、各タプルは(絵柄, 数字)の形式を持ちます。 - 絵柄は
char型、数字はu64型です。
input関数参照
let mut data: Vec<(char, u64)> = Vec::new(); // 入力されたカードの情報を格納するベクタ
バブルソート
alds1_02_C.rs
/* num: 要素の数, v: 入力されたカードの情報 */
fn bubbleSort(num: usize, v: &mut Vec<(char, u64)>) -> Vec<(char, u64)> {
let mut flag: bool = true;
while flag {
flag = false;
for i in (1..num).rev() {
if v[i].1 < v[i-1].1 {
let tmp: (char, u64) = v[i];
v[i] = v[i-1];
v[i-1] = tmp;
flag = true;
}
}
}
v.to_vec()
}
選択ソート
alds1_02_C.rs
/* num: 要素の数, v: 入力されたカードの情報 */
fn selectionSort(num: usize, v: &mut Vec<(char, u64)>) -> Vec<(char, u64)> {
for i in 0..num {
let mut minj: usize = i;
for j in i..num {
if v[j].1<v[minj].1 {
minj = j;
}
}
if i!=minj {
let tmp: (char, u64) = v[i];
v[i] = v[minj];
v[minj] = tmp;
}
}
v.to_vec()
}
安定性の判定
以下のis_stable関数はcorrect(安定なベクタ)とdata(判定したいベクタ)を引数に取ります。
alds1_02_C.rs
/* correct: 安定なベクタ, vec: 判定したいベクタ */
fn is_stable(correct: &Vec<(char, u64)>, vec: Vec<(char, u64)>) {
print(&vec); // print関数でvecを出力
for i in 0..correct.len() {
// (ベクタ名)[i].0 は絵柄、(ベクタ名)[i].1 は数字を表す
if correct[i].0!=vec[i].0 || correct[i].1!=vec[i].1 { // 安定でない場合
println!("Not stable"); // 結果の出力
return; // ここで関数を終了
}
}
println!("Stable"); // 結果の出力
}
D. シェルソート <Problem Link>
シェルソートとは
シェルソートは、データの間隔を空けて部分的な挿入ソートを行い、最終的に間隔を1にして完全にソートするアルゴリズムです。
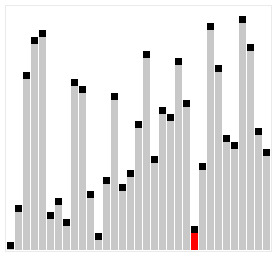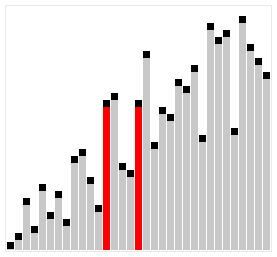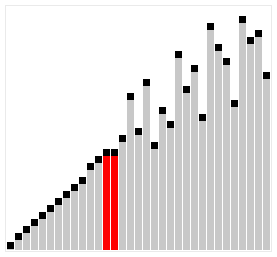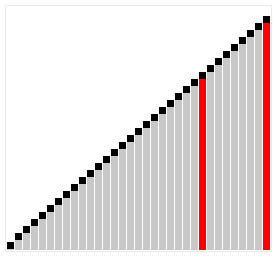
出典: Wikipedia シェルソート
シェルソート
以下のshellSort関数はシェルソートアルゴリズムを用いて、Aを昇順にソートします。
alds1_02_D.rs
/* num: 要素の数, A: 入力された数列 */
fn shellSort(num: usize, A: &mut Vec<u64>) {
let mut count = 0;
let G = generate_g(num); // ギャップの生成
for &i in &G { // iに各ギャップを代入
count += insertionSort(num, A, i as usize); // iに対して挿入ソートを実行
}
println!("{}",G.len()); // ギャップの数を出力
print(&G); // print関数でギャップの要素を出力
println!("{}",count); // 挿入回数を出力
}
ギャップの生成
以下のgenerate_g関数はギャップのベクタを生成します。
ギャップとは、シェルソートにおいて、要素を比較・交換する際の間隔のことを指します。
alds1_02_D.rs
/* num: 要素の数 */
fn generate_g(num: usize) -> Vec<u64> {
let mut g: Vec<u64> = Vec::new();
let mut element: u64 = 1; // ギャップの初期値を1に設定
while element<=num as u64 { // ギャップの生成
g.push(element); // ギャップをベクタに追加
element = element*3+1; // ギャップの更新
}
g.reverse(); // ベクタの要素を逆順にする
g // ギャップのベクタを返す
}
挿入ソート
alds1_02_D.rs
/* num: 要素の数, A: 入力された数列, g: ギャップ */
fn insertionSort(num: usize, A: &mut Vec<u64>, g: usize) -> usize {
let mut count = 0;
for i in g..A.len() {
let v = A[i];
let mut j = i;
while j>=g && A[j-g]>v { // ギャップの範囲内で挿入ソートを実行
A[j]=A[j-g];
j -= g;
count += 1; // 挿入回数をカウント
}
A[j] = v;
}
count // 挿入回数を返す
}
ALDS1-03
A. スタック <Problem Link>
以下のmain関数は標準入力から逆ポーランド記法で表された数式を読み込みます。
スタックは、データを一時的に保存するためのデータ構造で、後入れ先出し（LIFO: Last In, First Out）の原則に従います。(例：食器の重ね置き、本の積み重ねなど...)
後入れ先出し(LIFO)とは
後入れ先出し(LIFO)は、最後に追加されたデータが最初に取り出される特性を持っています。
出典: Wikipedia スタック
alds1_03_A.rs
use std::io::{self, BufRead};
fn main() {
let stdin = io::stdin(); // 標準入力の取得
let mut lines = stdin.lock().lines(); // 標準入力の行を取得
let mut input = lines.next().unwrap().unwrap(); // 標準入力からの読み込み
let mut stack: Vec<i64> = Vec::new(); // スタックを表すベクタの宣言
for symbol in input.split_whitespace() { // 入力を空白で分割しsymbolに代入
match symbol { // symbolの値によって場合分け
"+" => {
let b = stack.pop().unwrap(); // スタックから後ろの要素を2つ取り出す
let a = stack.pop().unwrap();
stack.push(a+b); // 加算してスタックに戻す
}
"-" => {
let b = stack.pop().unwrap(); // スタックから後ろの要素を2つ取り出す
let a = stack.pop().unwrap();
stack.push(a-b); // 減算してスタックに戻す
}
"*" => {
let b = stack.pop().unwrap(); // スタックから後ろの要素を2つ取り出す
let a = stack.pop().unwrap();
stack.push(a*b); // 乗算してスタックに戻す
}
num => {
let n = num.parse::<i64>().unwrap(); // 入力された数値をi64型に変換
stack.push(n); // スタックに数値を追加
}
}
}
let result = stack.pop().unwrap();
println!("{}", result);
}
B. キュー <Problem Link>
以下のmain関数は標準入力からプロセスの情報を読み込み、キューを使用してラウンドロビンスケジューリングを実行します。
キューは、データを一時的に保存するためのデータ構造で、先入れ先出し（FIFO: First In, First Out）の原則に従います。(例：列に並ぶ人、プリンタのジョブ待ちなど...)
先入れ先出し(FIFO)とは
先入れ先出し(FIFO)は、最初に追加されたデータが最初に取り出される特性を持っています。
出典: Wikipedia キュー (コンピュータ)
alds1_03_B.rs
fn main() {
let (q, mut queue) = input(); // input関数からプロセスの情報を取得
let mut total: i64 = 0;
while let Some(mut process)=queue.pop_front() { // キューからプロセスを取り出す
if process.1>q { // プロセスの残り時間がクオンタムより大きい場合
process.1 -= q; // プロセスの残り時間を更新
total += q; // 経過時間を更新
queue.push_back(process); // プロセスをキューの後ろに戻す
} else {
total += process.1; // 経過時間を更新
println!("{} {}", process.0, total); // プロセスの終了時間を出力
}
} // キューが空になるまでループ
}
C. 双方向連結リスト <Problem Link>
以下のdll関数は標準入力からコマンドを読み込み、双方向連結リストを操作します。
双方向連結リストは、各ノードが前後のノードへの参照を持つデータ構造です。これにより、リストの両端から効率的に要素の追加や削除が可能になります。
実装のポイント
-
VecDequeを使用して双方向連結リストを実現しています。 - 各コマンドに対して、リストの前後から要素を追加・削除する操作を行っています。
-
deleteFirstではリストの先頭から、deleteLastではリストの末尾から要素を削除します。 -
insertではリストの末尾に要素を追加します。 -
deleteでは指定された要素をリストから削除します。
alds1_03_C.rs
fn dll() -> VecDeque<i64> {
let mut word = String::new();
std::io::stdin().read_line(&mut word).unwrap();
let n: usize = word.trim().parse().unwrap(); // コマンドの数
let stdin = io::stdin();
let mut lines = stdin.lock().lines();
let mut list: VecDeque<i64> = VecDeque::new(); // 双方向連結リスト
for i in 0..n { // コマンドの数だけループ
let line = lines.next().unwrap().unwrap().trim().to_string();
let words = line.split_whitespace().collect::<Vec<&str>>();
match words[0] {
"deleteFirst" => { // リストの先頭から要素を削除
list.pop_back();
},
"deleteLast" => { // リストの末尾から要素を削除
list.pop_front();
},
"insert" => { // リストの末尾に要素を追加
let cmd: i64 = i64::from_str(words[1]).unwrap();
list.push_back(cmd);
},
"delete" => { // 指定された要素をリストから削除
let cmd: i64 = i64::from_str(words[1]).unwrap();
if let Some(remove_index) = list.iter().rposition(|x| *x == cmd) {
list.remove(remove_index);
}
},
_ => {}
}
}
list // 双方向連結リストを返す
}
D. Areas on the Cross-Section Diagram <Problem Link>
以下のcalc関数はstack(入力された模式断面図の情報)を引数に取ります。
スタックを用いて、入力された模式断面図の各谷間の面積を計算します。
実装のポイント
- スタックを使用して、'/'と'\'のペアを管理します。
- 各'/'に対して、対応する'\'を探し、その間の面積を計算します。
- 計算された面積は、スタックに保持されます。
alds1_03_D.rs
/* stack: 入力された模式断面図の情報('/', '\', '_'で表現) */
fn calc(stack: &mut Vec<(char, u64)>) {
let mut count = 0; // 現在の'/'に対する'\'の数
let mut process = 0; // 最後に処理された'/'のインデックス
let mut min = 0; // 最後に処理された'\'のインデックス
for i in 0..stack.len() {
count = 0;
if stack[i].0=='/' { // '/'の場合
for j in (0..i).rev() { // 逆順に探索
if stack[j].0=='\\' { // '\'の場合
count += 1; // 現在の'/'に対する'\'の数をカウント
process = j; // 最後に処理された'/'のインデックス
stack[i].0 = '_'; // 現在の'/'を'_'に置き換え
stack[j].0 = '_'; // 最後に処理された'\'を'_'に置き換え
stack[j].1 = count; // 最後に処理された'\'に対する'/'の数を記録
if process<min { // processがminより小さい場合
for i in process+1..=min {
// 最後に処理された'/'に対する'\'の数を加算
stack[process].1 += stack[i].1;
// 最後に処理された'\'に対する'/'の数をリセット
stack[i].1 = 0;
}
}
min = process; // 最後に処理された'\'のインデックス
break;
}
else if stack[j].0=='_' { // '_'の場合
count += 1; // 現在の'/'に対する'\'の数をカウント
}
}
}
}
}
ALDS1-04
A. 線形探索 <Problem Link>
以下のlinear_search関数は、与えられた数列から指定された値を線形探索で検索します。
線形探索とは
線形探索は、データ構造の先頭から順に要素を比較していく探索手法です。最悪の場合、探索対象の要素が見つかるまでにn回の比較が必要です。
参考資料: Wikipedia 線形探索
実装のポイント
- ベクタの先頭から順に要素を比較し、指定された値が見つかるまで探索を続けます。
- 2つのベクタSとTに対して、Tの各要素がSに存在するかどうかを確認します。
- search関数の戻り値を用いて、見つかった要素の数をカウントします。
alds1_04_A.rs
fn main() {
let (n, mut S) = input(); // input関数から配列Sの情報を取得
let (q, mut T) = input(); // input関数から配列Tの情報を取得
let mut count = 0;
S.push(0); // Sentinel valueを追加
for i in T {
count += search(n, &mut S, i); // Tの各要素に対してsearch関数を呼び出す
}
println!("{}",count); // 見つかった要素の数を出力
}
以下のsearch関数は、与えられたベクタから指定された値を線形探索で検索します。
実装のポイント
- 探索する値がベクタに存在するかどうかを線形探索で確認します。
- 探索する値が見つかった場合は1を、見つからなかった場合は0を返します。
alds1_04_A.rs
/* num: 要素の数, vec: 探索対象のベクタ, key: 探索する値 */
fn search(num: usize, vec: &mut Vec<u64>, key: u64) -> u64 {
let mut i: usize = 0;
vec[num] = key; // ベクタの最後にSentinel valueを設定
while vec[i]!=key { // Sentinel valueに達するまで探索を続ける
i += 1;
if i==num { // 探索が終了した場合
return 0; // 見つからなかった場合は0を返す
}
}
1 // 見つかった場合は1を返す
}
B. 二分探索 <Problem Link>
以下のbinary_search関数は、与えられた数列から指定された値を二分探索で検索します。
A問題と同様に、2つのベクタSとTに対して、Tの各要素がSに存在するかどうかを確認します。
戻り値を用いて、見つかった要素の数をカウントします。
:::details
二分探索は、ソートされたデータ構造に対して効率的に要素を検索する手法です。探索範囲を半分に分割し、目的の要素がどちらの範囲に存在するかを判断します。最悪の場合、探索対象の要素が見つかるまでにlog2(n)回の比較が必要です。
参考資料: Wikipedia 二分探索
:::
alds1_04_B.rs
/* num: 要素の数, vec: 探索対象のベクタ, key: 探索する値 */
fn binarysearch(num: usize, vec: &mut Vec<u64>, key: u64) -> u64 {
let mut i: usize = 0;
let mut right: usize = num; // 探索範囲の右端(初期値はベクタの最後尾)
let mut left: usize = 0; // 探索範囲の左端
while left<right { // 探索範囲が有効な間
let mid: usize = (right+left)/2; // 分割点のインデックス
if vec[mid]==key { // 探索する値が見つかった場合
return 1; // 見つかった場合は1を返す
}
else if key<vec[mid] { // 探索する値が分割点より小さい場合
right = mid; // 探索範囲の右端を更新
}
else { // 探索する値が分割点より大きい場合
left = mid+1; // 探索範囲の左端を更新
}
}
0 // 見つからなかった場合は0を返す
}
C. 辞書 <Problem Link>
以下のdictionary関数は標準入力からコマンドを読み込み、ハッシュセットを用いて辞書を操作します。
HashSet型とは
HashSet型は、Rustの標準ライブラリで提供されているデータ構造で、重複しない要素の集合を表現します。内部でハッシュテーブルを使用しており、以下の操作が効率的に行えます。
- insert: 要素を集合に追加します。
- remove: 要素を集合から削除します。
- contains: 要素が集合に含まれているかを確認します。
参考資料: Rust公式ドキュメント HashSet
alds1_04_C.rs
fn dictionary() {
let mut word = String::new();
std::io::stdin().read_line(&mut word).unwrap();
let n: usize = word.trim().parse().unwrap(); // コマンドの数
let stdin = io::stdin();
let mut lines = stdin.lock().lines();
let mut set: HashSet<String> = HashSet::new(); // ハッシュセットの初期化
for i in 0..n {
// 1行分のコマンドを読み込み、String型に変換
let mut line = lines.next().unwrap().unwrap().trim().to_string();
// 空白を削除し、コマンドを分割してベクタに格納
let words = line.split_whitespace().collect::<Vec<&str>>();
match words[0] {
"insert" => { // 挿入コマンド
set.insert(words[1].to_string()); // ハッシュセットに挿入
},
"find" => { // 検索コマンド
if set.contains(&words[1].to_string()) { // ハッシュセットを検索
println!("yes"); // 見つかった場合は"yes"を出力
} else {
println!("no"); // 見つからなかった場合は"no"を出力
}
},
_ => {}
}
}
}
D. 割り当て <Problem Link>
以下のallocation関数は荷物をトラックに積載するための最小の積載量を求めます。
alds1_04_D.rs
/* n: 要素の数, k: トラックの数, w: 各荷物の重さのベクタ */
fn allocation(n: usize, k: usize, w: &mut Vec<usize>) -> usize {
let mut left = *w.iter().max().unwrap(); // 各荷物の最大値を初期値とする
let mut right = w.iter().sum::<usize>(); // 各荷物の合計値を初期値とする
let mut mid = 0;
while left < right { // 二分探索の範囲が有効な間
mid = (left + right) / 2; // 分割点の更新
// 荷物をトラックに積載できるか判定
if canLoad(n, k, w, mid) { // 荷物をトラックに積載できる場合
right = mid; // 探索範囲の右端を更新
} else { // 積載できない場合
left = mid + 1; // 探索範囲の左端を更新
}
}
left // 最小の積載量を返す
}
以下のcanLoad関数は荷物をトラックに積載できるかどうかを判定します。
alds1_04_D.rs
/* n: 要素の数, k: トラックの数, w: 各荷物の重さのベクタ, capacity: トラックの積載量 */
fn canLoad(n: usize, k: usize, w: &Vec<usize>, capacity: usize) -> bool {
let mut trucks_used = 1;
let mut current_weight = 0;
for i in 0..n { // 各荷物に対してループ
if current_weight + w[i] <= capacity { // 現在の積載量に荷物を追加できる場合
current_weight += w[i]; // 現在の積載量を更新
} else { // 積載できない場合
trucks_used += 1; // 新しいトラックを使用
current_weight = w[i]; // 現在の積載量を更新
if trucks_used > k { // トラックの数が上限を超えた場合
return false; // 荷物を積載できないので、falseを返す
}
}
}
true // ループを抜けた場合、荷物を積載できるので、trueを返す
}
ALDS1-05
A. 総当たり <Problem Link>
以下のmakeCombination関数は、与えられた数列Aから、指定された値mを作れるかどうかを総当たりで判定します。
再帰関数とは
再帰関数とは、関数が自分自身を呼び出すことで問題を解決する手法です。再帰を用いることで、複雑な問題をよりシンプルなサブ問題に分割し、解決することができます。
alds1_05_A.rs
/* A: 与えられた数列のベクタ, m: 指定された値のベクタ, q: 値の数 */
fn makeCombination(A: Vec<u64>, m: Vec<u64>, q: usize) {
for i in m {
let mut flag = false;
for j in 0..q {
flag = rec(&A, i, j);
if flag {
println!("yes");
break;
}
}
if !flag { println!("no"); }
}
}
以下のrec関数は、再帰的に数列Aの要素を組み合わせて、指定された値restを作れるかどうかを判定します。
alds1_05_A.rs
/* A: 与えられた数列のベクタ, rest: 指定された値, start: 現在の位置 */
fn rec(A: &Vec<u64>, rest: u64, start: usize) -> bool {
if rest==0 { return true; } // 終了条件
else if start>=A.len() { return false; } // 終了条件
let result1 = rec(&A, rest, start+1); // 再帰呼び出し
let result2 = if rest>=A[start]{
rec(&A, rest-A[start], start+1) // 再帰呼び出し
} else { false }; // 終了条件
result1||result2 // 結果の論理和
}
B. マージソート <Problem Link>
以下のmerge関数は、マージソートアルゴリズムの一部であり、2つの部分配列を1つのソートされた配列に統合します。
マージソートとは
マージソートは、分割統治法に基づくソートアルゴリズムであり、配列を再帰的に分割し、ソートされた部分配列を統合することで全体をソートします。
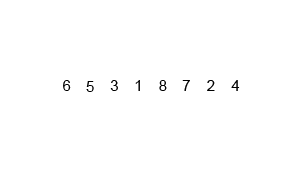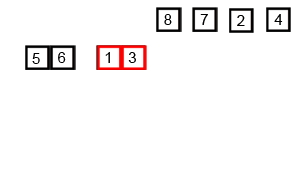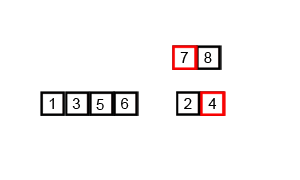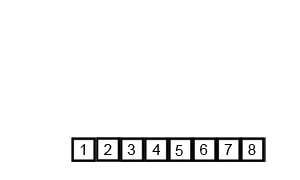
出典: Wikipedia マージソート
alds1_05_B.rs
/* A: 与えられた数列のベクタ, left: 左端, mid: 中央, right: 右端, count: 逆転した回数 */
fn merge(A: &mut Vec<u64>, left: usize, mid: usize, right: usize, count: &mut usize) {
let n1 = mid - left; // 左部分配列のサイズ
let n2 = right - mid; // 右部分配列のサイズ
let mut L: Vec<u64> = Vec::new();
let mut R: Vec<u64> = Vec::new();
for i in 0..n1 { L.push(A[left+i]); } // 左部分配列を作成
for i in 0..n2 { R.push(A[mid+i]); } // 右部分配列を作成
let inf = std::f64::INFINITY as u64;
L.push(inf); // 最大の値(無限大)を追加
R.push(inf); // 最大の値(無限大)を追加
let (mut i, mut j) = (0, 0);
for k in left..right { // マージ処理
if L[i]<=R[j] { // 左部分配列の要素が小さい場合
A[k] = L[i]; // 元の配列に値を戻す
i += 1;
*count += 1; // 逆転した回数をカウント
}else {
A[k] = R[j]; // 元の配列に値を戻す
j += 1;
*count += 1; // 逆転した回数をカウント
}
}
}
以下のmergeSort関数は、マージソートアルゴリズムを用いて、再帰的に数列Aを昇順にソートします。
alds1_05_B.rs
/* A: 与えられた数列のベクタ, left: 左端, mid: 中央, right: 右端, count: 逆転した回数 */
fn mergeSort(A: &mut Vec<u64>, left: usize, right: usize, count: &mut usize) {
if left+1<right {
let mid = (left + right) / 2; // 中央を計算
mergeSort(A, left, mid, count); // 左部分配列をソート
mergeSort(A, mid, right, count); // 右部分配列をソート
merge(A, left, mid, right, count); // マージ処理
}
}
C. コッホ曲線 <Problem Link>
以下のkock関数は、コッホ曲線を再帰的に計算し、各頂点の座標を出力します。
コッホ曲線とは
コッホ曲線は、自己相似性を持つフラクタル曲線の一種で、初期の線分を特定のルールに従って再帰的に分割することで生成されます。
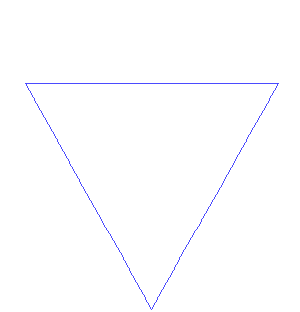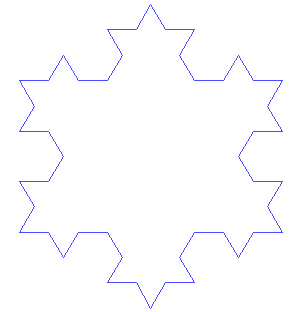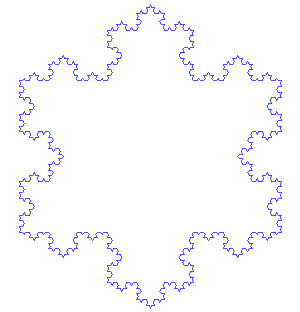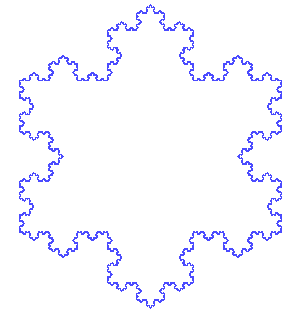
出典: Wikipedia コッホ曲線
alds1_05_C.rs
/* n: 再帰の深さ, p1: 始点, p2: 終点 */
fn kock(n: usize, p1: (f64, f64), p2: (f64, f64)) {
if n==0 { return; } // 再帰の終了条件
let rad: f64 = PI / 3.0;
let s: (f64, f64) = (
(2.0*p1.0 + 1.0*p2.0) / 3.0, // 新しい頂点sのx座標の計算
(2.0*p1.1 + 1.0*p2.1) / 3.0 // 新しい頂点sのy座標の計算
);
let t: (f64, f64) = (
(1.0*p1.0 + 2.0*p2.0) / 3.0, // 新しい頂点tのx座標の計算
(1.0*p1.1 + 2.0*p2.1) / 3.0 // 新しい頂点tのy座標の計算
);
let u: (f64, f64) = (
// 新しい頂点uのx座標の計算
(t.0 - s.0)*rad.cos() - (t.1 - s.1)*rad.sin() + s.0,
// 新しい頂点uのy座標の計算
(t.0 - s.0)*rad.sin() + (t.1 - s.1)*rad.cos() + s.1
);
kock(n-1, p1, s); // 新しい頂点の計算
println!("{} {}", s.0, s.1);
kock(n-1, s, u); // 新しい頂点の計算
println!("{} {}", u.0, u.1);
kock(n-1, u, t); // 新しい頂点の計算
println!("{} {}", t.0, t.1);
kock(n-1 , t, p2); // 新しい頂点の計算
}
D. 反転数 <Problem Link>
以下のコードは、マージソートを用いて配列の反転数を計算します。
反転数とは
反転数は、配列内の要素の順序が逆転しているペアの数を表します。例えば、配列 [2, 3, 1] では、(2, 1) と (3, 1) の2つの逆転が存在します。
参考資料: Wikipedia 転倒数
実装のポイント
逆転数の計算は、マージソートのマージ処理中に行われます。左部分配列の要素が右部分配列の要素より大きい場合、その左部分配列の要素と右部分配列の要素の間に存在するすべての要素が逆転しているとみなされます。
- L[i] > R[j] となった場合、L[i]以降の残り要素（n1 - i個）はすべてR[j]より大きいことがわかります。
- そのため、count += n1 - iを使うことで逆転数を一気にカウントすることができます。
alds1_05_D.rs
/* A: 与えられた数列のベクタ, left: 左端, mid: 中央, right: 右端, count: 逆転した回数 */
fn merge(A: &mut Vec<u64>, left: usize, mid: usize, right: usize, count: &mut usize) {
let n1 = mid - left; // 左部分配列の要素数
let n2 = right - mid; // 右部分配列の要素数
let mut L: Vec<u64> = Vec::new();
let mut R: Vec<u64> = Vec::new();
for i in 0..n1 { L.push(A[left+i]); } // 左部分配列のコピー
for i in 0..n2 { R.push(A[mid+i]); } // 右部分配列のコピー
let inf = std::f64::INFINITY as u64;
L.push(inf); // 最大の値(無限大)を追加
R.push(inf); // 最大の値(無限大)を追加
let (mut i, mut j) = (0, 0);
for k in left..right { // マージ処理
if L[i]<=R[j] { // 左部分配列の要素が小さい場合
A[k] = L[i]; // 元の配列に値を戻す
i += 1;
}else {
A[k] = R[j]; // 元の配列に値を戻す
j += 1;
*count += n1 - i; // 逆転数をカウント()
}
}
}
/* A: 与えられた数列のベクタ, left: 左端, right: 右端, count: 逆転した回数 */
fn mergeSort(A: &mut Vec<u64>, left: usize, right: usize, count: &mut usize) {
if left+1<right {
let mid = (left + right) / 2;
mergeSort(A, left, mid, count);
mergeSort(A, mid, right, count);
merge(A, left, mid, right, count);
}
}
ALDS1-06
A. 計数ソート <Problem Link>
以下のcountingSort関数は、計数ソートアルゴリズムを用いて、数列Aを昇順にソートします。
計数ソートとは
計数ソートは、整数の範囲が限られている場合に効率的に動作するソートアルゴリズムです。配列の各要素の出現回数をカウントし、その情報をもとにソートを行います。計数ソートは、安定ソートであり、O(n + k)の時間計算量を持ちます。ここで、nはソートする要素の数、kは入力の最大値です。
alds1_06_A
/* n: 要素の数, A: 入力された数列Aのベクタ, B: 出力される数列Bのベクタ */
fn countingSort(n: usize, A: &mut Vec<u64>, B: &mut Vec<u64>) {
let k = 10000;
let mut C: Vec<u64> = vec![0; k+1]; // 各要素の出現回数をカウントするためのベクタ
for &i in A.iter() { C[i as usize] += 1; } // 各要素の出現回数をカウント
for i in 1..k { C[i] += C[i-1]; } // 各要素の累積出現回数を計算
for &i in A.iter().rev() { // 元のベクタを逆順で処理
let a: usize = i as usize; // 現在の要素のインデックスを取得
C[a] -= 1; // 累積出現回数を減少
B[C[a] as usize] = i; // 出力するベクタに値を配置
}
}
B. Partition <Problem Link>
以下のpartition関数は、クイックソートアルゴリズムの一部であり、与えられた数列Aを基準値を中心に分割します。
alds1_06_B.rs
/* n: 要素の数, A: 与えられた数列のベクタ */
fn partition(n: usize, A: &mut Vec<u64>) -> usize{
let x = A[n-1]; // 基準値を設定
let mut i: usize = 0; // 分割位置の初期化
let mut tmp: u64 = 0; // 一時的な変数の初期化
for j in 0..n-1 { // 分割処理
if A[j]<=x { // 基準値以下の要素を前方に移動
i += 1;
// A[i-1]とA[j]を入れ替える
tmp = A[i-1];
A[i-1] = A[j];
A[j] = tmp;
}
}
// A[i]とA[n-1]を入れ替える
tmp = A[i];
A[i] = A[n-1];
A[n-1] = tmp;
i
}
C. クイックソート <Problem Link>
以下のquickSort関数は、partition関数を用いて、再帰的に数列Aを昇順にソートします。
クイックソートとは
クイックソートは、分割統治法に基づく効率的なソートアルゴリズムです。配列の要素を基準値（ピボット）を使って分割し、再帰的にソートを行います。平均的な計算量はO(n log n)ですが、最悪の場合はO(n^2)となることがあります。
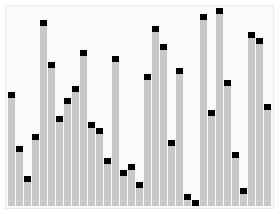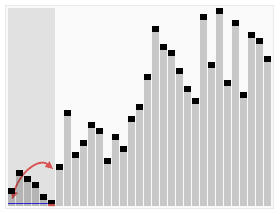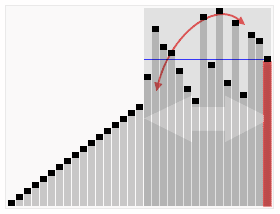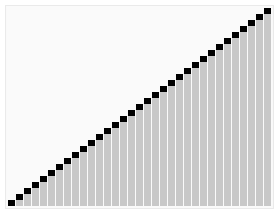
出典: Wikipedia クイックソート
alds1_06_C.rs
/* p: 左端のインデックス, r: 右端のインデックス, A: 与えられた数列のベクタ */
fn quickSort(p: usize, r: usize, A: &mut Vec<(char, u64, u64)>) {
if p<r {
let q: usize = partition(p, r, A); // 分割処理
quickSort(p, q-1, A); // 左部分を再帰的にソート
quickSort(q+1, r, A); // 右部分を再帰的にソート
}
}
/* p: 左端のインデックス, r: 右端のインデックス, A: 与えられた数列のベクタ */
fn partition(p: usize, r:usize, A: &mut Vec<(char, u64, u64)>) -> usize{
let x = A[r].1; // 基準値を設定
let mut i: usize = p-1; // 分割位置のインデックスの初期化
for j in p..r {
if A[j].1<=x { // 基準値以下の要素を前方に移動
i += 1; // 分割位置を進める
A.swap(i as usize, j as usize); // 要素を入れ替える
}
}
A.swap((i+1) as usize, r as usize); // 基準値を正しい位置に移動
i+1 // 新しい分割位置のインデックスを返す
}
以下のis_stable関数は、ソートされた数列が安定であるかどうかを判定します。
alds1_06_C.rs
/* vec: ソートされた数列のベクタ */
fn is_stable(vec: &Vec<(char, u64, u64)>) {
for i in 0..vec.len()-1 {
if vec[i].1==vec[i+1].1 && vec[i].2>vec[i+1].2 { // 安定ではない場合
println!("Not stable"); // メッセージを出力
print(&vec); // print関数で元の数列を出力
return;
}
}
// 安定している場合
println!("Stable"); // メッセージを出力
print(&vec); // print関数で元の数列を出力
}
D. Minimum Cost Sort <Problem Link>
以下のweigh関数は、最小のコストで数列をソートし、昇順に整列するコストの総和の最小値を計算します。
alds1_06_D.rs
/* W: 与えられた数列のベクタ, n: 要素の数 */
fn weigh(W: &Vec<u64>, n: usize) -> u64 {
// 各要素のインデックスを保持するハッシュマップをindexesとして作成
let mut indexes: HashMap<u64, isize> = HashMap::new();
let mut A = W.clone(); // WのコピーをベクタAとして作成
let mut weight = 0;
A.sort(); // Aをsort()関数でソート
let lowestwv = A[0]; // 最小の要素を取得
for (i, &w) in W.iter().enumerate() {
indexes.insert(w, i as isize); // 各要素のインデックスを保持
}
for i in 0..n {
if *indexes.get(&W[i]).unwrap() < 0 { // すでに処理済みの要素はスキップ
continue;
}
let fwv = W[i]; // Wのi番目の要素を取得
let mut av = A[i]; // Aのi番目の要素を取得
if fwv == av {
continue;
}
let mut minwv = fwv; // 最小の要素を取得
let mut next_idx = i; // 次のインデックスを初期化
let mut sum1 = 0; // 合計値を初期化
let mut count = 1; // カウントを初期化
while {
sum1 += W[next_idx]; // 合計値を更新
if minwv > W[next_idx] {
minwv = W[next_idx]; // 最小の要素を更新
}
if fwv == av { // もし元の位置と現在の位置が同じなら
false // falseを返す
} else { // それ以外の場合
count += 1;
// 次のインデックスを更新する(usize型に変換する)
next_idx = *indexes.get(&av).unwrap() as usize;
indexes.insert(av, -1); // すでに処理済みの要素としてマーク
av = A[next_idx]; // Aの次の要素を取得
true // trueを返す
}
} {}
let sum2 = sum1 + minwv + (count + 1) * lowestwv; // 新しい合計値を計算
sum1 += (count - 2) * minwv; // 合計値を更新
weight += sum1.min(sum2); // 最小の合計値を選択
}
weight // 最小コストを返す
}
まとめ
以上で、ALDS1の各セクションに対応するRustでの実装例を紹介しました。
私がご紹介したコードは、あくまで一例ですので参考にしていただかなくて構いません。
私のGitHubリポジトリには、ALDS1(01~13)までの実装が含まれていますので、皆様の学習に役立てていただければ幸いです。
- GitHubリポジトリ: hashisato/alds1-rust
Discussion