Zenn
💻

Graph Neural Networks

2022/05/23に公開
ディープラーニング
graph
CNN
gcn
tech

はじめに

私自身グラフ理論や計算機科学といった分野に精通している人間ではないので定義や解釈が厳密ではない可能性があります．
また論文等でよく出てくる単語に関しては英語表記のまま記述しています．
あくまで機械学習としてのGraph Neural Networkを理解するための解釈をしています．

そもそもGraphとは

ざっくり理解

graph構造のデータとしてよく挙げられるのがSNSのユーザ間のつながりや論文の引用関係，タンパク質の構造などたくさんあるが，重要なのは ある点とある点の関係を線で結んで表現できる構造である ということだ．
簡単のために相互フォローであり，関係性に方向はない（無向グラフ）としてSNSのつながりを表現するとFig.1のようになる．

Fig.1 SNSのユーザ間のつながり
このユーザーをnode V，フォローの関係をedge Eといい，graph Gを=(V, E)と表現する．(ノード数はNとする)

より具体的に

Fig.1でSNSのユーザー間の繋がりを例に挙げたのでこれを深掘りしていく．

Step 1 Edgeをmatrixで表現する

まず，図のままだと数学的・プログラミング的に扱いにくいのでmatrixで表現していく．
つながりを表現するときに用いられるのがadjacency matrixである．
このmatrixは\mathbf{A}で表されることが多く，その要素A_{ij}が頂点{i}から頂点{j}への辺が存在する時は1、辺が存在しない時は0となるN \times Nの正方行列である．
例えば，AとBは繋がっているのでA_{1,2}=1となる．
これを図で表現するとFig.2のようになる．

Fig.2 adjacency matrix

Step 2 Nodeをmatrix表現する

ユーザーが無個性な訳がないので普通はnodeも特徴を持っている．
ここでは例として以下のような属性を付与してみる．

  • 趣味のジャンル（0-1）: 趣味に費やす時間のうち，運動，芸術，ゲームの割合を示す．合計で1になるように割り当てる
  • スポーツが好きか（0 or 1）: スポーツが好きなら，そうでないなら0
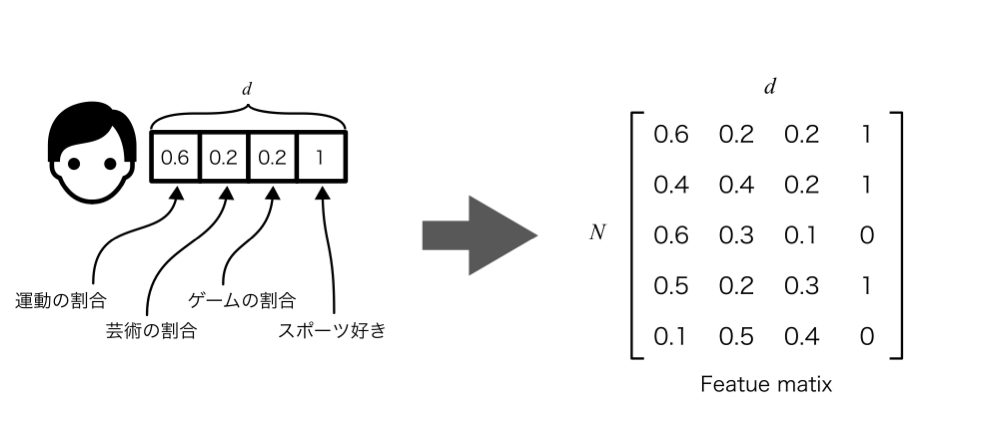
    特徴を増やしすぎてもややこしくなるのでこの程度でおさめておく．このような特徴を格納した配列をfeature matrixといい，特徴の数をdとするとN \times dの行列\mathbf{X}として表現される．このgraph全体のfeature matrixはFig.3のように表される．

    Fig.3 feature matrix

この章のまとめ

  • graphというのはnodeとedgeで構成される情報のこと．
  • nodeとedgeにはそれぞれ情報があり，それらはmatrixで表現される．

Graph Neural Network

Graph Convolutional network

Graph Neural Networkで最も一般的に用いられる手法がGraph Convolutionalである．
これは基本的には画像のConvolutionalと同じで近傍の特徴に重みを掛け合わせて特徴を集約するといった手法である．
画像と違う点は大きく以下の２点である．

  1. node間に位置の関係がない
  2. 中心のnode自身の特徴の扱いが違う

1. node間に位置の関係がない

画像では画素の位置を考慮してたたみ込んでいる．例えばFig.4のように3 \times 3のカーネルを用いた場合9つの異なる重みを用いて畳み込んでおり，数式で表すと以下のようになる.

h_{x,y} = \sum_i \sum_j w_{i,j}x_{x+i,y+j}


Fig.4 convolution for image
一方グラフでは，FIg.5のようにBさんからみてAもDもEもただのSNSのフォロワーであり，そこに区別はない．そのため画像のようにそれぞれに対応した3つの重み(B-A，B-D，B-E)で畳み込むのではなく，共通の1つの重みで畳み込む．

h_v = \sum_{w \in N(v)} Wx_w

ここでN(v)は隣接ノードであり，この場合N(3)=\{A, D, E\}である．

Fig.5 graphの畳み込み

2. 中心のnode自身の特徴の扱いが違う

中心のnodeについては大きく２通りの方法があり，近接nodeと同じ重みで畳み込む方法と独立した重みで畳み込む方法がある．
同じ重みで畳み込む場合\tilde{N}(3)=\{A, B, D, E\}と変更し以下のように定義する

h_v = \sum_{w \in \tilde{N}(v)} Wx_w

独立した重みで畳み込む場合は以下のように定義する．

h_v = W_1x_v + \sum_{w \in N(v)} W_2x_w


Fig.6 中心node自身の畳み込み

matrixを使って表現すると

説明が簡単なので，中心nodeを近接nodeと同じ重みで畳み込む場合で説明していく．
中心nodeが近接nodeと同じということはadjacency matrixの対格成分（self-loop）が追加されるのと同義である．よって\tilde{A} = A+Iと定義をし直すと，

h_v = \sum_{w \in \tilde{N}(v)} Wx_w\\ \downarrow \\ \mathbf{H} = \tilde{\mathbf{A}}\mathbf{X}\mathbf{W}^{\mathrm{T}}

簡単のため\mathbf{W}=Iとすると以下のように計算できる

\begin{bmatrix} 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 \end{bmatrix} \times \begin{bmatrix} 0.6 & 0.2 & 0.2 & 1. \\ 0.4 & 0.4 & 0.2 & 1. \\ 0.6 & 0.3 & 0.1 & 0. \\ 0.5 & 0.2 & 0.3 & 1. \\ 0.1 & 0.5 & 0.4 & 0. \end{bmatrix}\\= \begin{bmatrix} 1.6 & 0.8 & 0.5 & 2. \\ 1.7 & 1.3 & 0.7 & 2. \\ 0.7 & 0.7 & 0.3 & 0. \\ 1.5 & 0.8 & 0.7 & 3. \\ 1. & 1.1 & 0.7 & 2. \end{bmatrix}

Normalize

画像の畳み込みは常に畳み込む数が同じだが，graphの場合はそうもいかない．Fig.1のようにAさんは2つ，Bさんは3つ，Cさんは1つのnodeとつながっているように，nodeによって隣接nodeの数が様々である．そこでつながっているnodeの数で割ることによって正則化を行う．

h_v = \frac{1}{n(\tilde{N}(v))} \sum_{w \in \tilde{N}(v)} Wx_w

この数式の\frac{1}{n(\tilde{N}(v))} \sum_{w \in \tilde{N}(v)}の部分はadjacency matrixとdegree matrix \mathbf{D}を用いてFig.7のように定義できる

Fig.7 degree matrixによる正則化
よって

h_v = \frac{1}{n(\tilde{N}(v))} \sum_{w \in \tilde{N}(v)} Wx_w \\ \downarrow \\ \mathbf{H} = \tilde{\mathbf{D}}^{-1}\tilde{\mathbf{A}}\mathbf{X}\mathbf{W}^{\mathrm{T}}

ただし，この正則化方法も論文によって様々提案されており，Semi-Supervised Classification with Graph Convolutional Networksという論文では以下のような形状で提案されている．

\mathbf{H} = \tilde{\mathbf{D}}^{-\frac{1}{2}}\tilde{\mathbf{A}}\tilde{\mathbf{D}}^{-\frac{1}{2}}\mathbf{X}\mathbf{W}^{\mathrm{T}}

そしてこの\mathbf{H}を次の入力\mathbf{X}とすることで2個先のnode，さらに次の入力とすることで3個先のnodeの情報を集約していく．

この章のまとめ

  • 基本的にはCNNと考え方は同じ
  • graphの特性（位置情報がない，中心nodeと近傍node）に合わせた拡張がされている
  • nodeによって畳み込む数が違うので正規化されている

最後に

最近話題のGraph Neural Neteworkについて自分なりにまとめてみました．
比較的新しい手法であることもあり，日本語の記事が少なく理解に苦しんだのでこの記事が誰かの理解の手助けになれば幸いです．

Discussion