マルコフ方程式(x^2+y^2+z^2=3xyz)の正の整数解を求めるアルゴリズムを実装してみた

はじめに

この世にはマルコフ方程式というものがあるそうです。マルコフのディオファントス方程式とも言うらしいです（よく知らない）

https://www.youtube.com/watch?v=PgGckE4Qw64

マルコフ方程式とは、

$$x^2 + y^2 + z^2 = 3xyz$$

のことで、この方程式の正の整数解について、 $(x, y, z) = (1, 1, 1)$ から再帰的に生成できるということを知りました。

おもしろそうだったので実装してみることにしました。

マルコフ方程式の解き方

全然証明はしないのですが、マルコフ方程式は、なんと、前の項の $3xz -y$ または $3yz - x$が次の項の一部として使えるみたいです。具体的には、次の項が $(x, z, 3xz - y)$または$(y, z, 3yz -x)$として決まるようです。

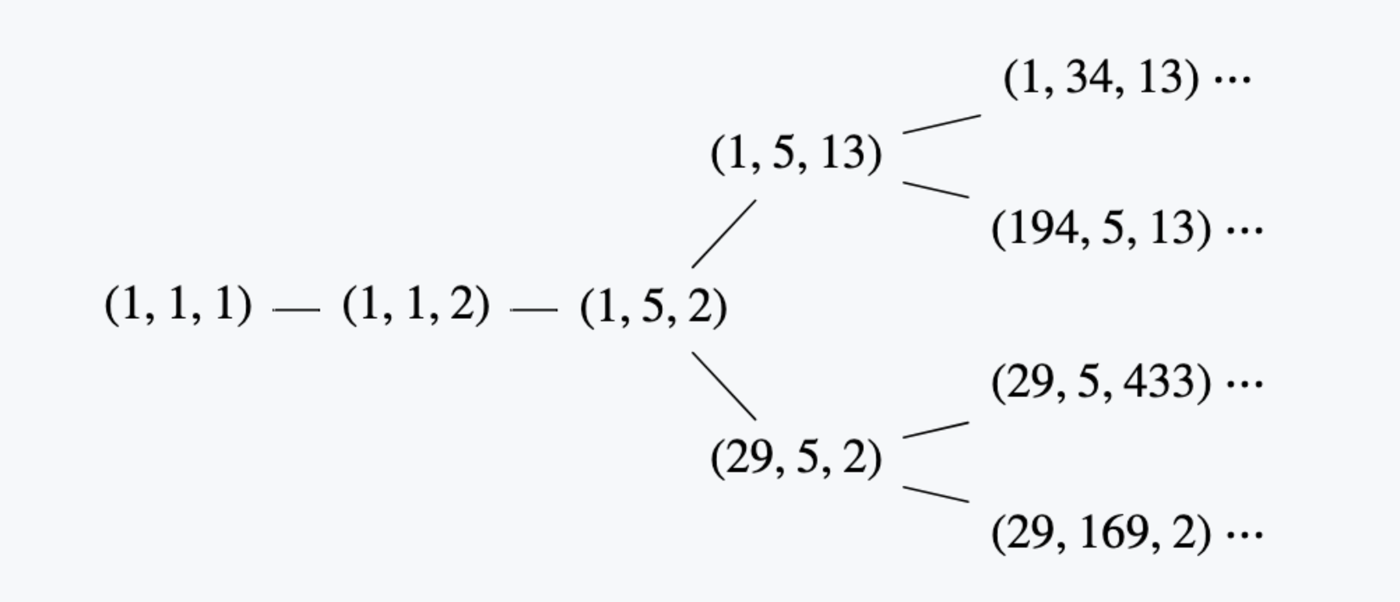
（https://mathlog.info/articles/2647 から引用させていただきました）

この図（マルコフ木というらしい）のようにドンドンと解が決まっていくみたいです。すごい！

たとえば、 $(1, 5, 13)$ だったら、

$$1^2+5^2+13^2 = 1 + 25 + 169 = 195 = 5 * 39 = 3 * 1 * 5 * 13$$

というようになってすごいです。

書いたコード

そういうわけでコードを書いてみました。

基本的には再帰で解いていき、すでに存在する組があったときは無視するというようなことをしています。冗長ですが$(1, 1, 1)$とか$(1, 1, 2)$から生成されるときには、同じ組が2通り出てしまうので排除用に入れています。$(1, 1, 1), (1, 1, 2), (1, 2, 5)$を最初の組にして、フィボナッチ数列的にしてもいいのかもしれません。

SHOULD_PRINT = True
seed = (1, 1, 1)

cache = set()

def solve(n):
    if n == 1:
        if SHOULD_PRINT:
            print(*seed)
        cache.add(seed)
        return [seed]

    prev_ans_list = solve(n - 1)

    ans_list = []
    for prev_ans in prev_ans_list:
        # x z -> new_y
        new_y = 3 * prev_ans[0] * prev_ans[2] - prev_ans[1]
        # y z -> new_x
        new_x = 3 * prev_ans[1] * prev_ans[2] - prev_ans[0]

        ans1 = (prev_ans[0], prev_ans[2], new_y)
        ans2 = (prev_ans[1], prev_ans[2], new_x)

        if (ans1 not in cache):
            ans_list.append(ans1)
            cache.add(ans1)
        if (ans2 not in cache):
            ans_list.append(ans2)
            cache.add(ans2)

        if SHOULD_PRINT:
            if ans1 == ans2:
                print(*ans1)
            else:
                print(*ans1)
                print(*ans2)
    return ans_list


N = int(input())
solve(N)
# display answers as sorted tuples
# print(sorted(cache))

こんな感じで出力できました。

$ echo 5 | python3 markov_equation.py
1 1 1
1 1 2
1 2 5
1 5 13
2 5 29
1 13 34
5 13 194
2 29 169
5 29 433

心配なのでテストを入れたところ、深さ18まではいい感じに動いているっぽいです。O(2^N)なので、Nが多いと解けなくなります。

cache = set()

while True:
    try:
        x = input()
    except EOFError:
        print('ok')
        exit()
    a = list(map(int, x.split()))

    t = tuple(sorted(a))
    if t in cache:
        raise Exception('Already existed', t)
    cache.add(t)
    assert a[0] * a[0] + a[1] * a[1] + a[2] * a[2] == 3 * a[0] * a[1] * a[2], a

コード置き場

https://github.com/harukaeru/markov_equation