🍆

証明支援システムLeanに入門する #2

2023/10/26に公開2件

math

ここからはLeanを記述する際の実際の動きを確認していきます．
Natural number gameというものの存在は知っていたのですが，今回はプログラミング言語という側面からLeanを知っていきたいと思ったので，純粋なリファレンスを読み進めていこうと思います．

Lean4のリファレンスはWork in Progressだとありましたが，入門には問題なさそうなので公式のWebサイトに用意されている Lean Manual を読んでいきます．簡単な和訳をしながら，自分の思ったことを記述していくような記事になる予定です．Leanに関して無知な人間が思ったことを雑に書いていく記事なので，嘘や根拠のない予想が多く含まれます．この記事に書かれていることを鵜呑みにしないように注意をお願いします．

1. What is Lean

Leanがプログラミング言語であることから始まり，Leanの特徴が書かれています．文法に関する簡単な紹介もあります．

-- Defines a function that takes a name and produces a greeting.
def getGreeting (name : String) := s!"Hello, {name}! Isn't Lean great?"

関数の定義はdefキーワードを用いて行い，引数は(name: Type)と取るようです．詳細は後の章に任せて読み流していきます．

その下にはLeanが持つ機能についての記述があり，

型推論
一階関数
強力なデータ型
パターンマッチング
型クラス
モナド
文法拡張
健全なマクロ
依存型
メタプログラミング
マルチスレッド
証明

と，様々な機能を持つことが書かれています．Haskellをよく書く私としてはワクワクする言葉が並びます．

2. Tour of Lean

この章では具体的なコードを読み書きしながらLeanの主な機能を学ぶようです．Leanには関数，型という２つの重要な概念が存在するとも書かれています．

Function and Namespaces

Leanのプログラムの最も基本的な部分は，名前空間に属する関数だといいます．様々な働きをする関数たちをグループ分けする最も基礎的な方法として名前空間が用意されています．

namespace Besic Functions

これが名前空間の定義です．

def sampleFunction1 x := x*x + 3
def result1 := sampleFunction1 4573

先に確認したようにLeanは関数型の言語ですので，定数も関数と同じ文法で同じように定義します．(定数は引数を持たない定数関数と解釈されます．)
ここでは $\mathrm{sampleFunction}1: x\mapsto x^2+3$ と $\mathrm{result}1:=\mathrm{sampleFunction}1(4573)$ が定義されました．

#eval 2 + 2    -- 4が出力される
#eval println! "The result of squaring the integer 4573 and adding 3 is {result1}"

Leanでは文字列中に{}を入れることで文字列の埋め込みができるようです．{}の中に文字列でないものが入ってもきちんとキャストされています．型クラスの概念が用意されていると書いていたので，恐らくHaskellのShowに対応するような型クラスがあるのだと思います．
#evalコマンドは，与えられた式を解釈して標準出力に出力するコマンドみたいです．
println!はそれ自身が標準出力に出力しているような気がするのですが，具体的にどういう動作をしているのかは今は考えないことにしておきます．println!は返り値のないマクロで，#evalにマクロが与えられたときは式の解釈のみをするのかなぁと予想をして次に進みます．

def sampleFunction2 (x : Nat) := 2*x*x - x + 3
def result2 := sampleFucntion2 (7 + 4)

Leanには型推論が用意されているとのことでしたが，当然必要ならば型を明示することもできるみたいです．NatはNatural numberで自然数の意味です．

簡単な条件分岐も出てきました．

def sampleFunction3 (x : Int) :=
  if x > 100 then
    2*x*x - x + 3
  else
    2*x*x + x - 37

非常に完結でわかりやすい文法です．プログラミングの経験が少しでもある方にはもはや説明することもほぼありません．

if expression then
    trueのときの処理
else
    falseのときの処理

という文法を持つようです．if文全体が式として処理され，関数の返り値を与えているのもポイントです．

end BasicFunctions

名前空間が閉じられました．

def twice (f : Nat → Nat) (a : Nat) :=
  f (f a)

さて，関数を引数に持つ関数が現れました．fは自然数から自然数への関数であり，aは自然数です．twiceはaに対してfを二回適用する関数だと読み取れます．

#eval twice (fun x => x + 2) 10

funキーワードは無名関数の宣言に使われています．シンプルで良いです．

theorem twiceAdd2 (a : Nat) : twice (fun x => x + 2) a = a + 4 :=
  rfl

早速他の言語にはあまりない予約語が登場しました．どうやら，theoremというキーワードで定理を宣言できるようです．今回の定理はfun x => x + 2を二回適用するとfun x => x + 4になるという主張です．では証明を，と思ったのですが，rflの一言で閉じられています．Leanには強力な自動証明系が備わっており，記号的な操作で証明が完了してしまうような命題については自動で証明してくれるようです．強い．

#eval twice (· + 2) 10

・ + 2はfun x => x + 2の糖衣構文だと書かれています．数学でも偶に書くプレースホルダが使えるようです．わかりやすくて嬉しいです．

inductive Weekday where
  | sunday    : Weekday
  | monday    : Weekday
  | tuesday   : Weekday
  | wednesday : Weekday
  | thursday  : Weekday
  | friday    : Weekday
  | saturday  : Weekday

「列挙型はinductiveの特別なパターンです」とありますが．inductiveをまだ知らないのでよくわかりません．とりあえず列挙型に固有のデータ型が与えられているわけではなく，より一般的な型が存在するのだと思っておくことにします．(Weekdayって8回も書くのマジ？となっています)
こう書くことで，Weekday名前空間の中にsunday〜saturdayのコンストラクタが定義されるようです．

#check Weekday.sunday
#check Weekday.monday

#checkコマンドは与えられた引数の型を表示してくれます．この例ではこのように出力されました．

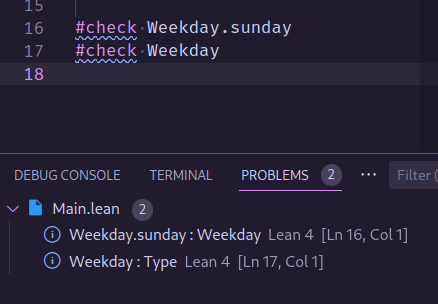
当然，Weekdayの型はTypeとなりました．

open Weekday
#check sunday
#check tuesday

openコマンドを使うことで名前空間を展開でき，名前空間の指示なしに中身を参照できるようになります．

def natOfWeekday (d : Weekday) : Nat :=
  match d with
  | sunday    => 1
  | monday    => 2
  | tuesday   => 3
  | wednesday => 4
  | thursday  => 5
  | friday    => 6
  | saturday  => 7

この関数はパターンマッチングを用いてWeekdayからNatへの変換を行います．

def isMonday : Weekday → Bool :=
  fun
    | monday => true
    | _      => false

こちらの関数は少々難解です．コメントによればこれは

fun d => match d with 
  | monday => true
  | _ => false

の糖衣構文だということです．無名関数の引数をそのままパターンマッチングの引数に流す操作をシンプルにかけるようになっています．また，関数の本体が無名関数になっていることで，isMonday自身には引数がないように見えているのもポイントです．

eval toString 10
#eval toString (10, 20)

文字列へキャストする関数はtoStringで提供されているようです．
文字列へキャストできる型クラスはToStringで定義されていました．

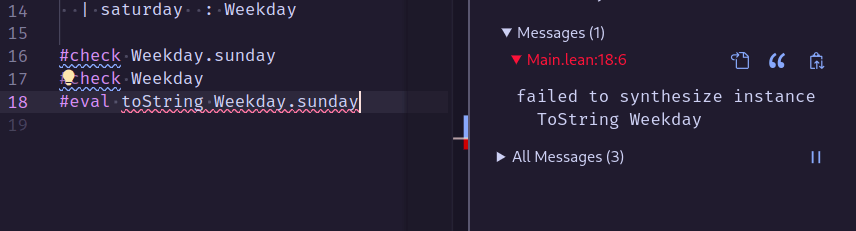
ToStringのインスタンスの実装も簡単に行なえます．

instance : ToString Weekday where
  toString (d : Weekday) : String :=
    match d with
    | sunday    => "Sunday"
    | monday    => "Monday"
    | tuesday   => "Tuesday"
    | wednesday => "Wednesday"
    | thursday  => "Thursday"
    | friday    => "Friday"
    | saturday  => "Saturday"

やはりパターンマッチングを使用しています．

def Weekday.next (d : Weekday) : Weekday :=
  match d with
  | sunday    => monday
  | monday    => tuesday
  | tuesday   => wednesday
  | wednesday => thursday
  | thursday  => friday
  | friday    => saturday
  | saturday  => sunday

Weekdayという名前空間にnext関数を定義しています．

#eval Weekday.next Weekday.wednesday
#eval next wednesday

先にWeekday名前空間をopenしたので，指定がなくとも参照できていることがわかります．

def Weekday.previous : Weekday -> Weekday
  | sunday    => saturday
  | monday    => sunday
  | tuesday   => monday
  | wednesday => tuesday
  | thursday  => wednesday
  | friday    => thursday
  | saturday  => friday

theorem Weekday.nextOfPrevious (d : Weekday) : next (previous d) = d :=
  match d with
  | sunday    => rfl
  | monday    => rfl
  | tuesday   => rfl
  | wednesday => rfl
  | thursday  => rfl
  | friday    => rfl
  | saturday  => rfl

この定理は「ある日の次の日の前の日」がある日と一致することを述べていますが，やはり記号的操作で完結するので自動的に証明が完了します．
また，

theorem Weekday.nextOfPrevious' (d : Weekday) : next (previous d) = d := by
  cases d
  all_goals rfl

とすればパターンマッチングを記述することなく証明が完了します．実際にLean Infoviewで確認したところ，casesにより全てのパターンが展開され，各々がゴールに設定され，all_goalsは全てのゴールに対して同じ操作を，今回であればrflを適用して証明終了，という流れでした．

さて，大まかな流れは掴めてきたので，次回は 4. Theorem Proving in Lean の指示に従ってTheorem Proving in Lean 4を読み進めようと思います．

Discussion

lean ja 2023/10/27

Theorem proving in lean4 は日本語訳もありますよ。https://aconite-ac.github.io/theorem_proving_in_lean4_ja/title_page.html

ハーツホーン 6ヶ月前

なんと，そうだったのですね．ありがとうございます．