乱数アルゴリズムについて
はじめに
ユニークなIDを登録する場合、128bitのランダムな数値であるバージョン4のUUIDがよく使われています。このUUIDは同じIDが被る衝突確率が限りなく低く、安全にユニークな値を得られます。どれくらいの確率かというと約3*10^17回UUIDを作っても99%の確率で、連続して一個も被らずUUIDを作れる可能性があるというくらい低い確率です。そんなUUIDについて上長と話していた時に、一つの疑念が思い浮かびました。
「完全に一様なランダムアルゴリズムがあれば128bitもいらないんじゃないか?」
UUIDの6bit分は決まってるので数の総数的には2^122個の数値があり、総数が多いから被る確率が低いのであって、乱数が一様であれば128bitもいらないのは一考の余地があると感じました。(64bitで計算したところ約6000万回UUIDを作った場合、99%の確率で連続して一個も被らずUUIDを作れる可能性がありますが、高々6000万回で100人に1人のユーザーがID生成に引っかかるというのは多いんじゃないかと思います。)
乱数アルゴリズムは多種多様に存在します。完全にランダムな数を出力するには、量子物理学の観点からなら得ることができるなどと言われておりますが、一様な乱数アルゴリズムは存在していると調べたらわかりました。そんな一様な乱数アルゴリズム、一様でない乱数アルゴリズムを少し検証してみたいと思います。
検証方法
- 0~1をランダムで出力する
- 3000回ランダムの数値を出力する
- 数値の分布を計測し、ばらつき具合を確認する
- 数値はランダム数列
x_{0} x_{1} \cdots x_{n} n=2999 x_{i} x_{i+1} x_{i+2}
線形合同法
線形合同法は擬似乱数生成式の一つで以下の漸化式で出力されます。
線形合同法の特徴についてですが、この手法は周期性を持っています。例えば周期が3の場合で、2,0,1というように乱数を出したあと、また2,0,1,2,0,1,・・・というように連続します。周期が短いと乱数には見えません。ただ周期の最大値をMにする必要十分条件があって、そのように変数a,c,Mを設定すると周期が長くなって同じ数が出る頻度が下がります。その必要十分条件は以下になります。
- cとMが互いに素(cとMの最大公約数が1)
- a-1がMを割り切る全ての素数の倍数
- Mが4の倍数であればa-1も4の倍数
一見難しそうな条件ではありますが、cをMの公約数ではない素数にしてaをM+1にすれば簡単に最大周期をMにすることができます。
この線形合同法は一様な乱数アルゴリズムではありますが、多次元疎結晶構造を生じやすく、周期が簡単に予測できるので、乱数と呼ぶには規則的すぎると思います。例えばa=M+1としてやると、
このように表せて、簡単に推測ができるようになってしまいます。なのでa,c,Mの数値を適当に決める必要があります。
では以下のスクリプトで分布を確認していきます。
%matplotlib widget
import numpy as np
import matplotlib.pyplot as plt
import random
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.widgets import Slider
# 初期値
rand = 65539
# 係数
A=1664525
C=1
M=4294967296
def func_rand(x):
inx=(A * x + C) % M
return int(inx)#(inx+1)/(M+2)
numbers_x = np.zeros(3000)
numbers_y = np.zeros(3000)
numbers_z = np.zeros(3000)
for i in range(3000):
rand = func_rand(rand)
numbers_x[i]=rand/M
numbers_y[(i+1) % 3000]=rand/M
numbers_z[(i+2) % 3000]=rand/M
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(numbers_y, numbers_x, numbers_z,s=1)
plt.show()
結果、以下のような散布図になりました。
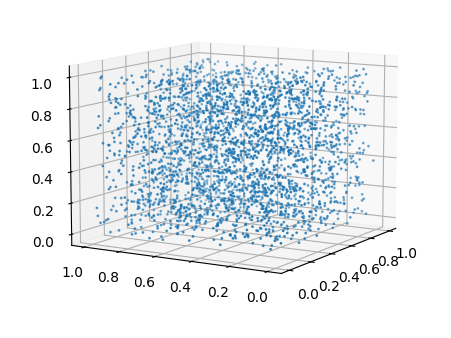
ばらつきがあり、規則性が見当たらない乱数が一目でわかります。しかし、これは係数がいい場合の散布図です。係数
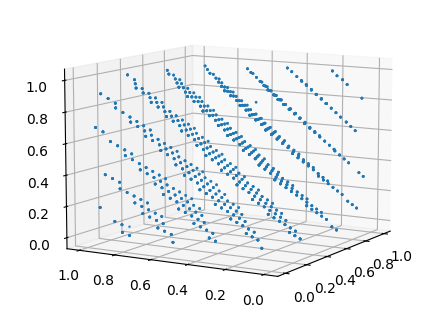
このように係数を悪くすると明らかに規則的で、乱数とは言えないような数値が出力されます。なので先ほども言ったように、線形合同法を使用する際は、係数を適当に決定する必要があります。しかし、線形合同法は後に紹介する手法より計算量が軽く、一番早い手法ではあります。
Twisted GFSR法
Twisted GFSR法はLFSR法(Linear Feedbacked Shift Register)を発展させたGFSR法(General Feedbacked Shift Register)をさらに発展させた手法です。順番に各手法についてみていきたいと思います。まずLFSR法は以下の式で表されます。
LFSR法は連続する
最後にTwisted GFSR法は上記の式の一部にフロベニウスの同伴行列のAで攪拌させることで、周期の上限を拡大したものになります。
Twisted GFSR法は以下の漸化式で出力されます。
これにより、GFSR法では周期の上限が
では以下のスクリプトで分布を確認していきます。
%matplotlib widget
import numpy as np
import matplotlib.pyplot as plt
import random
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.widgets import Slider
# パラメータの設定
p = random.randrange(2, 31)
q = random.randrange(1, p-1)
x = np.zeros([3000, 2**5])
# x_pまでの乱数を設定し、2進数で表現
for i in range(p):
rand = bin(random.randrange(0, 4294967296))
init_num = 2**5-len(list(rand[2:]))
x[i,init_num:] = np.array(list(rand[2:]))
# 同伴行列Aの設定
A = np.zeros([2**5, 2**5])
for i in range(A.shape[0]-1):
A[i,i+1] = 1.
a = bin(random.randrange(0, 4294967296))
init_num_a = 2**5-len(list(a[2:]))
A[-1,init_num_a:] = np.array(list(a[2:]))
# 2進数でのp以降の乱数決定
for i in range(x.shape[0]-p):
x[i+p,:] = (x[i+q,:] + np.dot(x[i,:],A))%2
# 2進数を10進数で1以下に変更して出力
def func_rand(j):
num = 0
for k in range(x.shape[1]):
num += x[j,k]*2**(-1-k)
return num
numbers_x = np.zeros(3000)
numbers_y = np.zeros(3000)
numbers_z = np.zeros(3000)
for i in range(3000):
rand = func_rand(i)
numbers_x[i]=rand
numbers_y[(i+1) % 3000]=rand
numbers_z[(i+2) % 3000]=rand
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(numbers_y, numbers_x, numbers_z,s=1)
plt.show()
結果、以下のような散布図になりました。
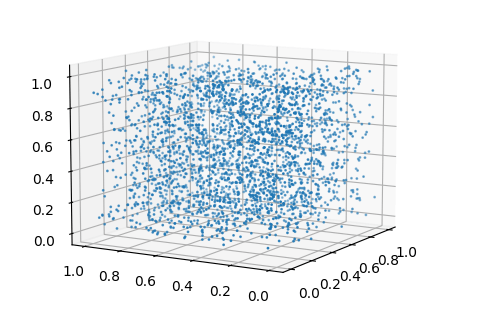
ばらつきがある散布図になりました。
python標準のrandom関数
pythonの乱数生成で扱われてるアルゴリズムは、メルセンヌ・ツイスタ法というアルゴリズムが使用されています。この乱数生成には乱数シードを設定することができ、同じシードの値を使用すると、全く同じ数を出力することができます。デフォルトのシード値は現在時刻などを参照しており、時間帯が別だと同じシード値にはなりません。
以下のスクリプトでばらつきを確認していきます。
import numpy as np
import matplotlib.pyplot as plt
import random
def func_rand():
return random.random()
numbers_x = np.zeros(3000)
numbers_y = np.zeros(3000)
numbers_z = np.zeros(3000)
for i in range(3000):
rand = func_rand()
numbers_x[i]=rand
numbers_y[(i+1) % 3000]=rand
numbers_z[(i+2) % 3000]=rand
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(numbers_x, numbers_y, numbers_z,s=1)
plt.show()
結果、以下のような散布図になりました。
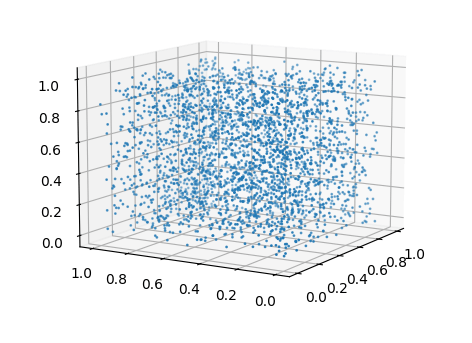
Twisted GFSR法と同様のばらつき具合になりました。
メルセンヌ・ツイスタ法
pythonのランダム関数とアルゴリズム上のメルセンヌ・ツイスタ法で違いは出るか試してみます。メルセンヌ・ツイスタ法は以下の漸化式によって出力されます。
ここでの行列B,Cは
このAはTwisted GFSR法で使用した行列Aです。
この手法で乱数を
メルセンヌ・ツイスタ法も同様に予測可能ではあります。また初期状態空間に0が多いと、しばらくの間出力にも0が多くなる傾向があるそうです。
では以下のスクリプトでばらつきを確認していきます。
%matplotlib widget
import numpy as np
import matplotlib.pyplot as plt
import random
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.widgets import Slider
numbers_x = np.zeros(3000)
numbers_y = np.zeros(3000)
numbers_z = np.zeros(3000)
randoms = np.zeros(3000)
p = 624
q = 397
a = 0x9908b0df
M = 4294967296
# 初期値
init = int(random.randrange(0, 4294967296))
randoms[0] = init
numbers_x[0] = init/M
numbers_y[1] = init/M
numbers_z[2] = init/M
index = int(random.randrange(0, 4294967296))
# 初期の乱数x_623まで設定
for j in range(1,p):
randoms[j]= int((index * (int(randoms[j-1]) ^ (int(randoms[j-1]) >> 30)) + j) & 0xffffffff)
numbers_x[j] = randoms[j]/M
numbers_y[j+1] = randoms[j]/M
numbers_z[j+2] = randoms[j]/M
# x_624以降を決定
def func_rand(k):
# k+1の下位31ビットとkの上位1ビットを足してx'_kを作成
num = (int(randoms[k+1]) & 0x7fffffff) + (int(randoms[k]) & 0x80000000)
# 乱数の値を決定
if num & 0x1 == 0:
randoms[k+p] = int(numbers_x[k+q]) ^ (num >> 1)
else:
randoms[k+p] = int(numbers_x[k+q]) ^ ((num >> 1) ^ a)
return randoms[k+p]
for i in range(3000-p):
rand = func_rand(i)
numbers_x[i+p]=rand/M
numbers_y[(i+p+1) % 3000]=rand/M
numbers_z[(i+p+2) % 3000]=rand/M
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(numbers_y, numbers_x, numbers_z,s=1)
plt.show()
結果、以下のような散布図になりました。
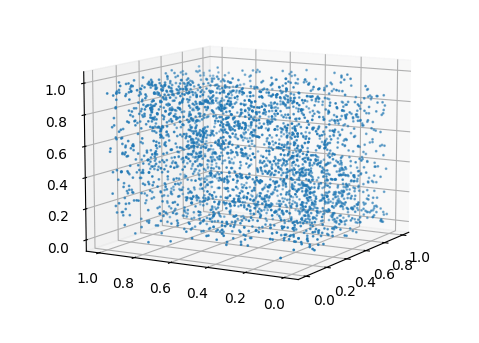
Twisted GFSR法やランダム関数と同様のばらつき具合になりました。
まとめ
ランダムアルゴリズムを見てきましたが、この記事でご紹介したものは全て擬似乱数生成機と言われてます。この擬似乱数生成機以外に、真性乱数生成機というノイズを用いる方法があります。熱のノイズや電気のノイズ、トンネル効果などを用いた量子的な確率的振る舞いなどを用いるそうです。それらのノイズの情報をエントロピーが低くなるまで掻き集めて、乱数として返して生成します。これらは時間がかかりますが値を予測しにくいです。(意図的に外から負荷をかけると予測が立てられることもあります)
というように乱数にも色々種類があって、手法により特徴があることを知れました。
Discussion