😇
歩行時の加速度,角速度データから歩行軌跡を描いてみた
最近センサデータを用いて屋内推定をするために勉強しており今回は加速度と角速度から歩行軌跡を描いたのでその方法を書く.言語はPythonを使用している.
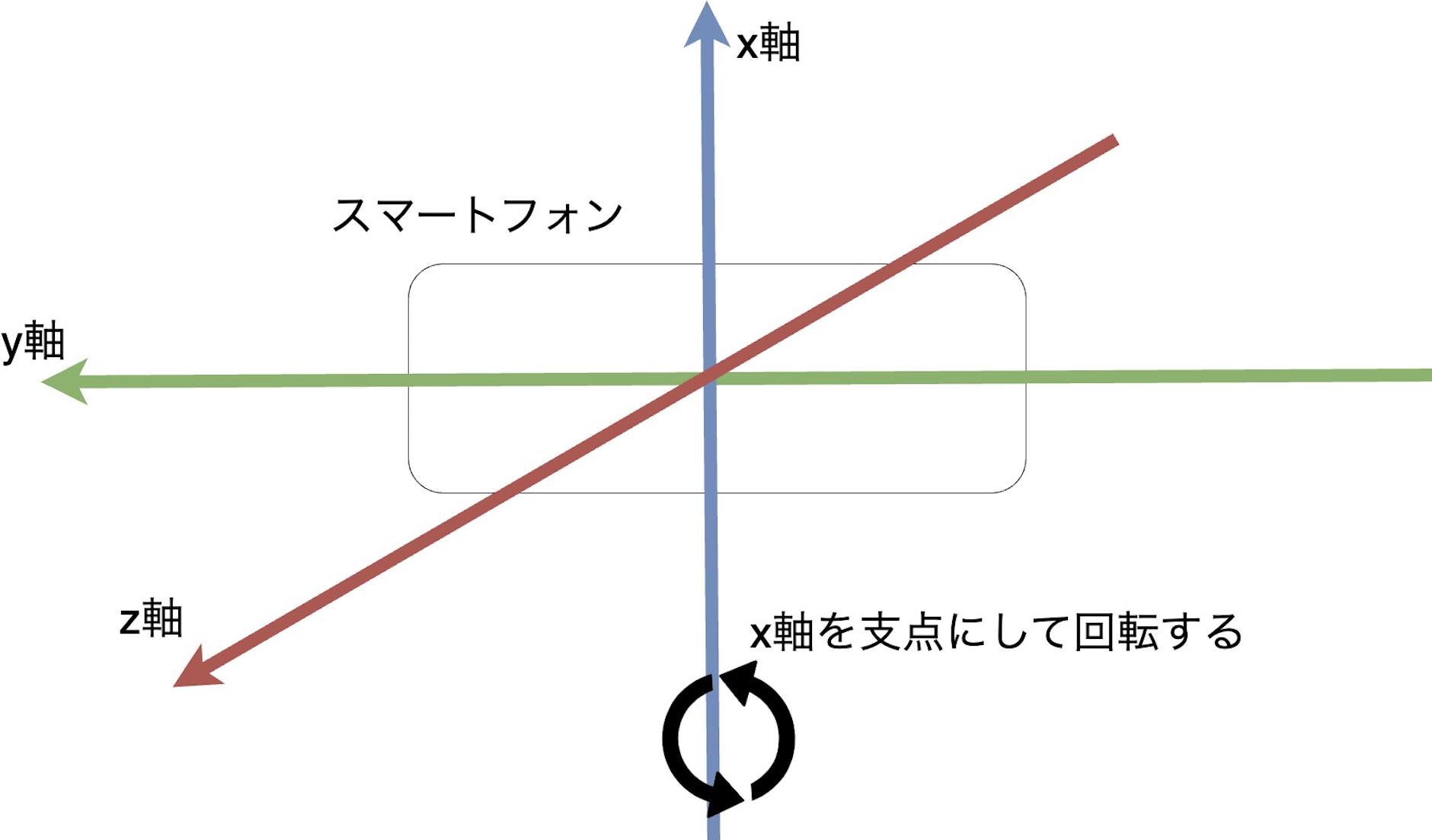
実験環境 * スマートフォン(iPhoneXR)を下記画像のようなポーチに入れ腰に巻き付けた状態で行う．そのためスマホの向きは横向きで装着される．
- センシング動作は9歩直進した後,左に90度回転し5歩歩くという動作を行う.
- 加速度，角速度の取得には複数のセンサを同時に取得できるいるアプリphyphoxを使用する．iOS,Android共に提供されている.
- 歩行データをわかりやすくするために開始時，終了時に約5秒の時間を空ける．
- サンプリング周波数は100Hz，つまり0.01秒ごとにセンサデータを取得する．
phyphoxの画面(カスタム実験で加速度とジャイロスコープを組み合わせる)
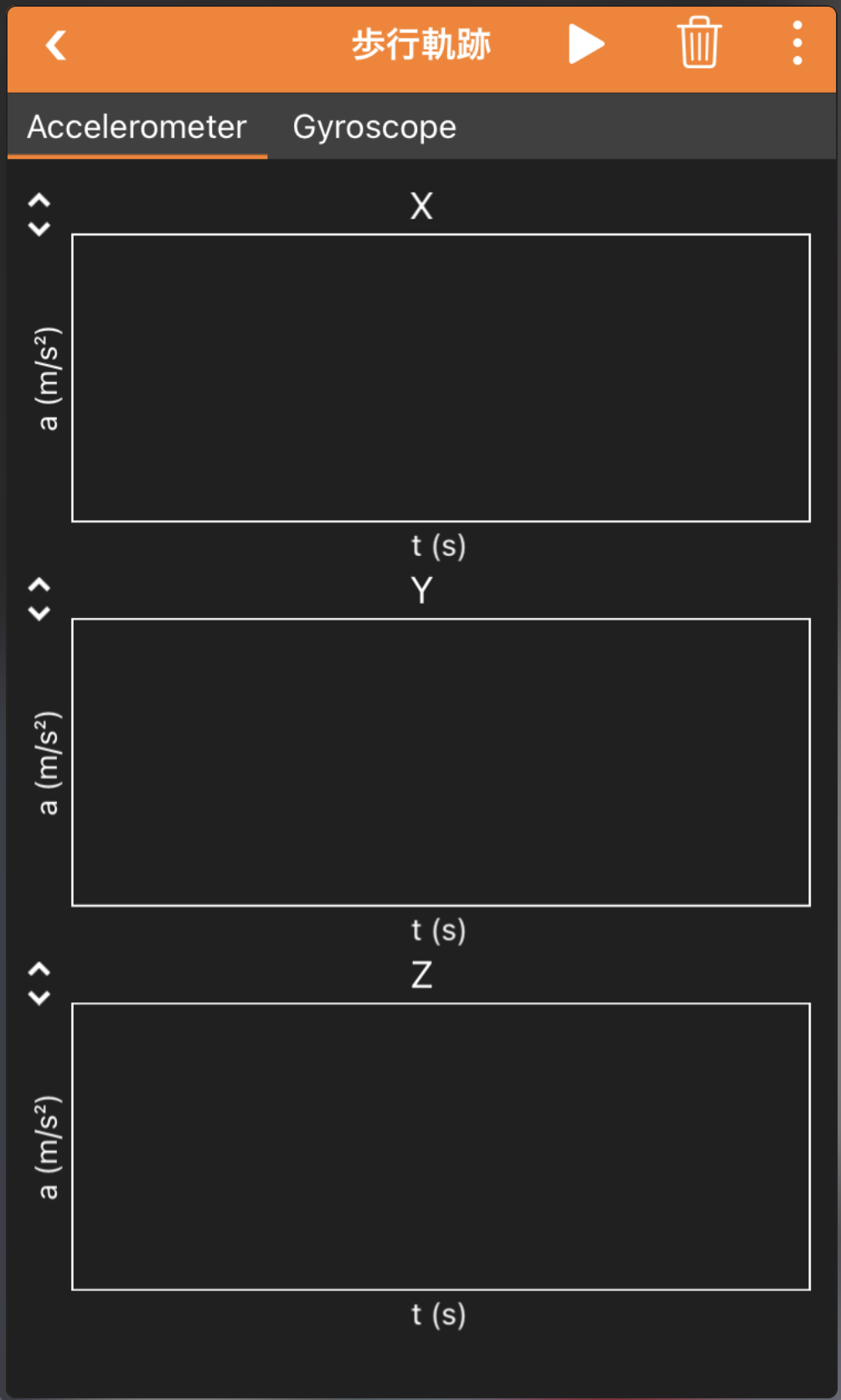
歩数推定
まずphyphoxで取得できた加速度のCSVファイルを見る．
Accelerometer.csv
"Time (s)","X (m/s^2)","Y (m/s^2)","Z (m/s^2)"
1.176791673E-3,8.904233551E0,-3.556604004E-1,4.019890594E0
1.125279168E-2,8.780890045E0,-3.487747192E-2,3.921844482E0
2.132879167E-2,8.837322693E0,1.197509766E-1,3.613186340E0
3.140579167E-2,9.055568848E0,5.284011841E-2,3.378474426E0
4.148179168E-2,9.088799744E0,2.619552612E-2,3.555256805E0
...
後のコードで扱いやすくするために最初のカラム名を変更する
Accelerometer.csv
"t","x","y","z"
1.176791673E-3,8.904233551E0,-3.556604004E-1,4.019890594E0
1.125279168E-2,8.780890045E0,-3.487747192E-2,3.921844482E0
2.132879167E-2,8.837322693E0,1.197509766E-1,3.613186340E0
3.140579167E-2,9.055568848E0,5.284011841E-2,3.378474426E0
4.148179168E-2,9.088799744E0,2.619552612E-2,3.555256805E0
...
今回の歩行推定にはノルムを利用する．ノルムはx,y,z軸の加速度を二乗し，それらの和の平方根を取ったものである.ノルムを利用すればデバイスの向きが変わったとしても加速度が同じならば常に一定になる．そのためより特定の軸を利用するよりも一貫した歩行推定が可能である．
Norm=√(x^2 + y^2 + z^2)で取得できる．
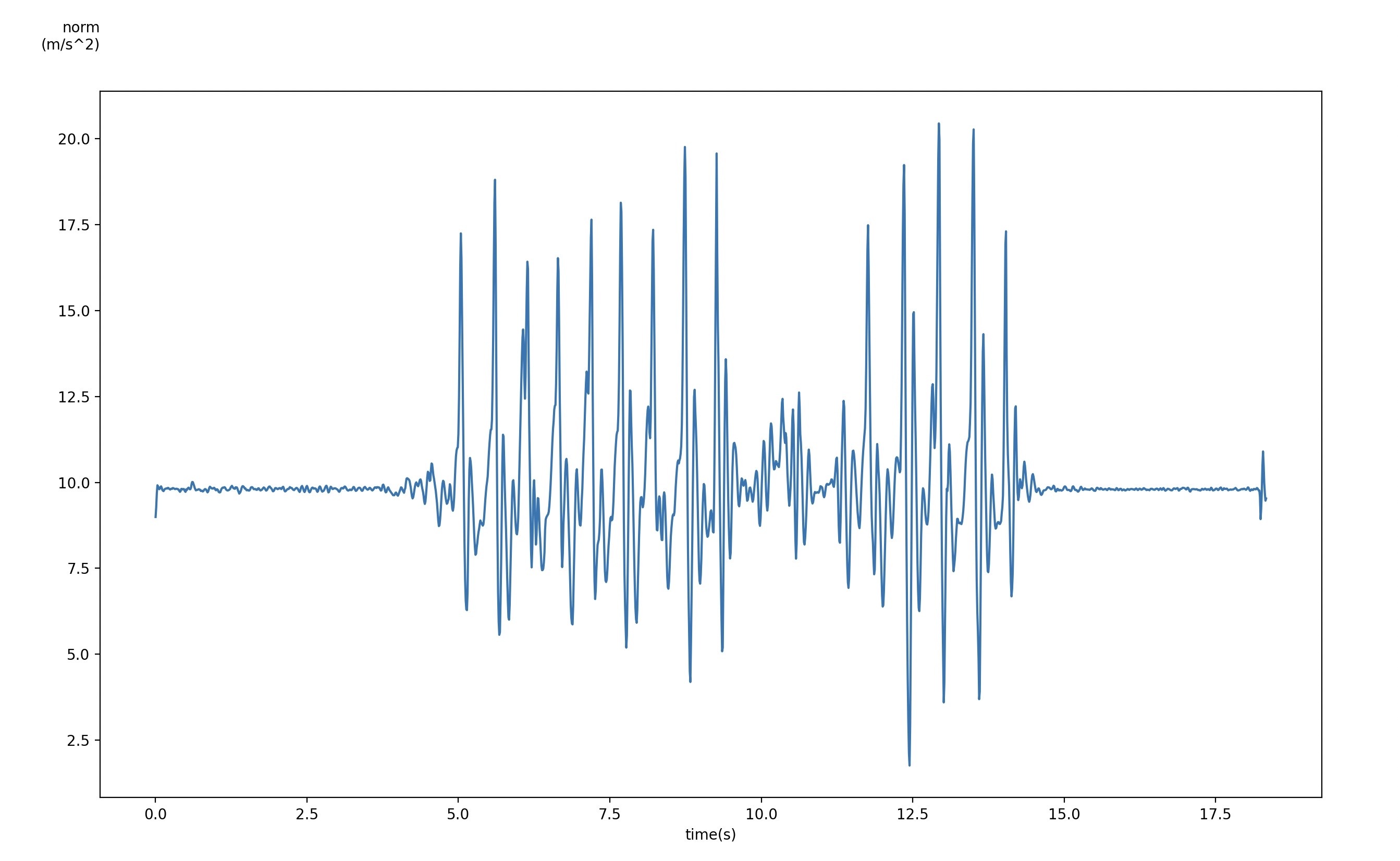
加速度のNormを求めて経過時間(t)による遷移をグラフに表示するコード
norm.py
import pandas as pd
import matplotlib.pyplot as plt
if __name__ == '__main__':
df = pd.read_csv('./data/Accelerometer.csv')
# normを計算
df['norm'] = (df['x']**2 + df['y']**2 + df['z']**2)**0.5
plt.plot(df['t'], df['norm'], zorder=1)
plt.xlabel('time(s)')
plt.ylabel('norm\n(m/s^2)', rotation=0, ha='right', va='top')
# Y軸ラベルの位置を調整
plt.gca().yaxis.set_label_coords(0, 1.1)
plt.show()
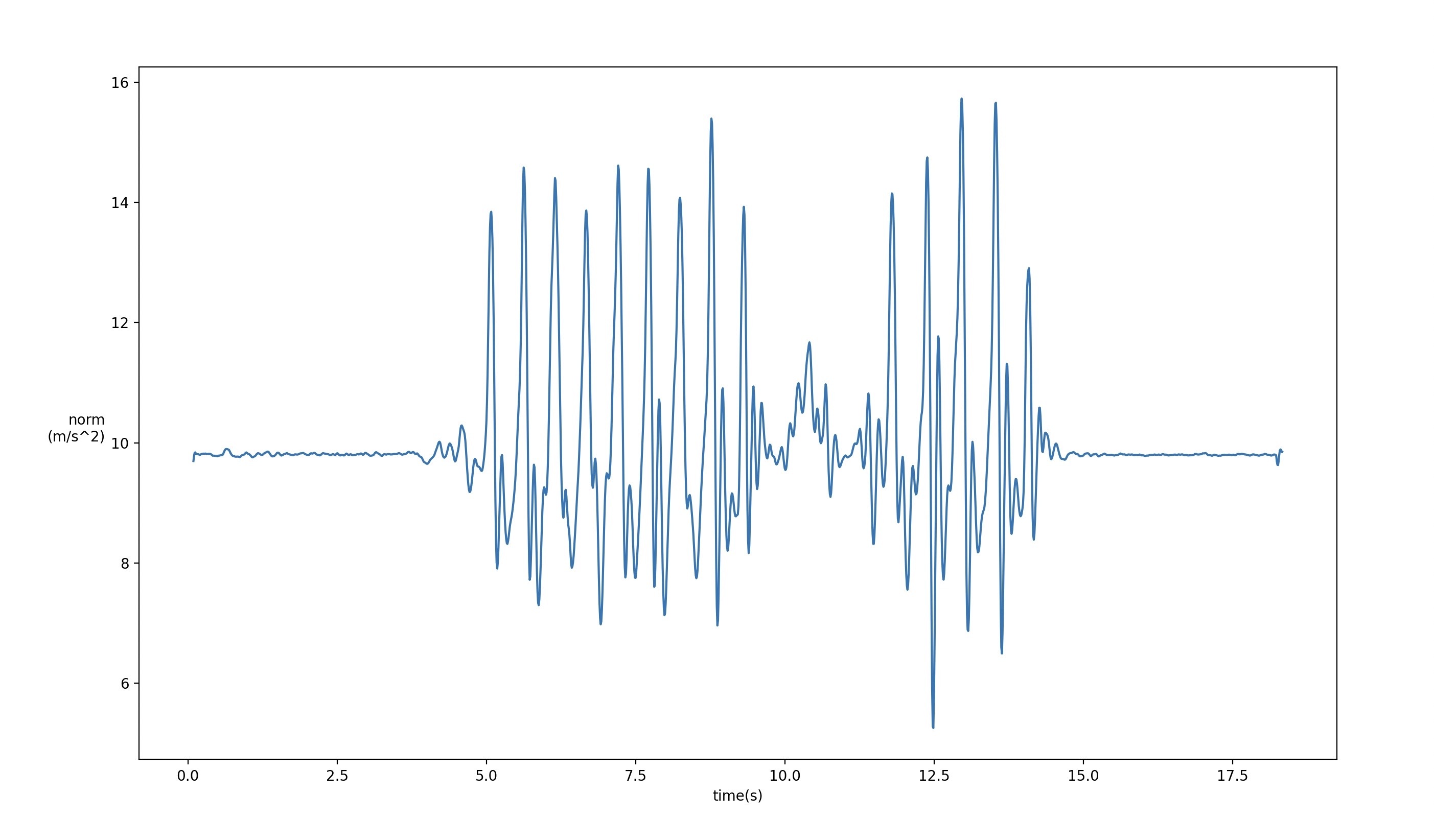
歩行信号は低周波成分なのでローパスフィルターをかけノイズを軽減する.
今回は移動平均フィルターを使用する.
lowpass.py
import pandas as pd
import matplotlib.pyplot as plt
if __name__ == '__main__':
df = pd.read_csv('./data/Accelerometer.csv')
# normを計算
df['norm'] = (df['x']**2 + df['y']**2 + df['z']**2)**0.5
df['low_norm'] = df['norm'].rolling(window=10).mean()
plt.plot(df['t'], df['low_norm'], zorder=1)
plt.xlabel('time(s)')
plt.ylabel('norm\n(m/s^2)', rotation=0, ha='right', va='top')
# Y軸ラベルの位置を調整
plt.gca().yaxis.set_label_coords(0, 1.1)
plt.show()
高周波成分が減少している．
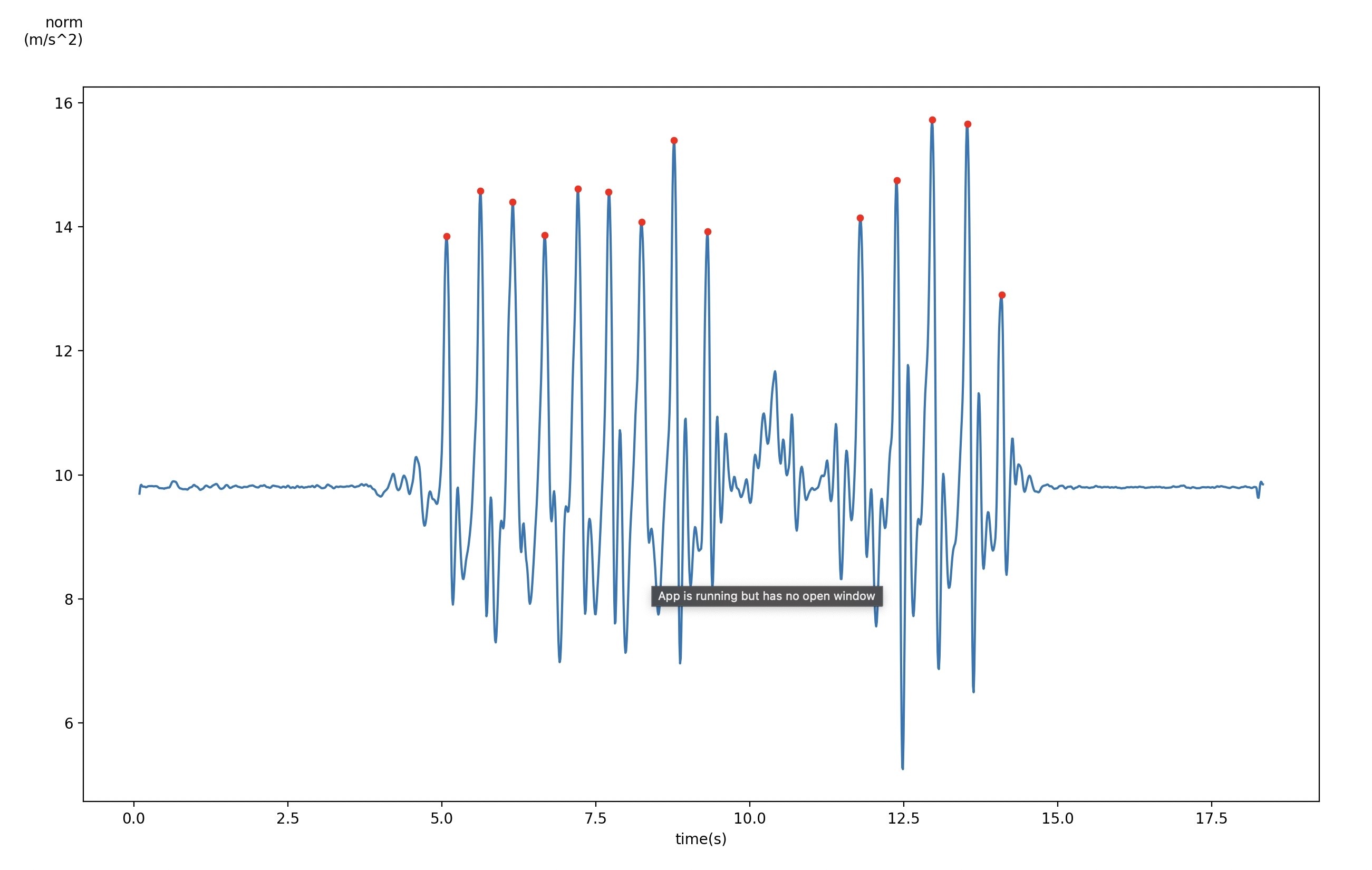
ピーク値を求め歩数を推定する．
可視化されたグラフからnormが12(m/s^2)以上の場合一歩と判定する.
peek.py
import pandas as pd
import matplotlib.pyplot as plt
from scipy import signal
if __name__ == '__main__':
df = pd.read_csv('./data/Accelerometer.csv')
# normを計算
df['norm'] = (df['x']**2 + df['y']**2 + df['z']**2)**0.5
df['low_norm'] = df['norm'].rolling(window=10).mean()
plt.plot(df['t'], df['low_norm'], zorder=1)
plt.xlabel('time(s)')
plt.ylabel('norm\n(m/s^2)', rotation=0, ha='right', va='top')
# Y軸ラベルの位置を調整
plt.gca().yaxis.set_label_coords(0, 1.1)
peek, _ = signal.find_peaks(df['low_norm'], height=12)
# 赤点を描画
plt.scatter(df['t'][peek], df['low_norm']
[peek], s=15, color='red', zorder=2)
plt.show()
9歩+5歩の歩数推定ができている．
歩行方向の推定
歩行軌跡をグラフで表現するには，どの方向に進んだのかを示す角度を求める必要がある．角速度データを利用して，進行方向の角度を計算できる．今回の実験では，スマートフォンを横向きに体に取り付けているため，x軸の角速度データを用いて進行方向の角度が求められる．
角速度のCSVファイル
Gyroscope.csv
"Time (s)","X (rad/s)","Y (rad/s)","Z (rad/s)"
8.547250007E-3,-6.150873378E-2,-6.603101641E-2,2.339305729E-2
1.862424999E-2,2.087008394E-2,-8.130924404E-2,1.806256361E-2
2.870025000E-2,8.376302570E-2,-4.760587960E-2,9.836326353E-3
...
これも先ほどと同じようにカラム名を変更する．
Gyroscope.csv
"t","x","y","z"
8.547250007E-3,-6.150873378E-2,-6.603101641E-2,2.339305729E-2
1.862424999E-2,2.087008394E-2,-8.130924404E-2,1.806256361E-2
2.870025000E-2,8.376302570E-2,-4.760587960E-2,9.836326353E-3
...
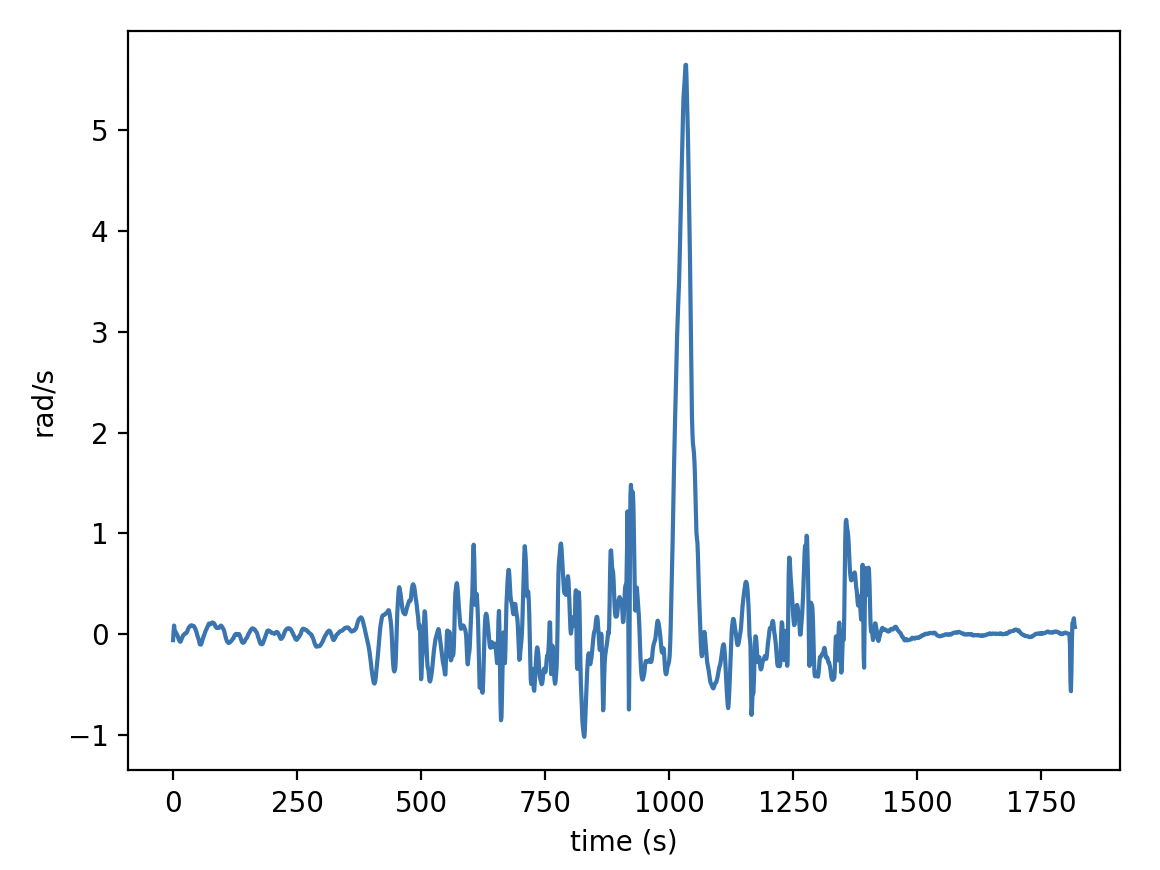
x軸の角速度と経過時間tのグラフ．
angular_velocity_x.py
import pandas as pd
import matplotlib.pyplot as plt
if __name__ == '__main__':
gyro_data = pd.read_csv('./data/Gyroscope.csv')
plt.xlabel('time (s)')
plt.ylabel('rad/s')
plt.plot(gyro_data['x'])
plt.show()
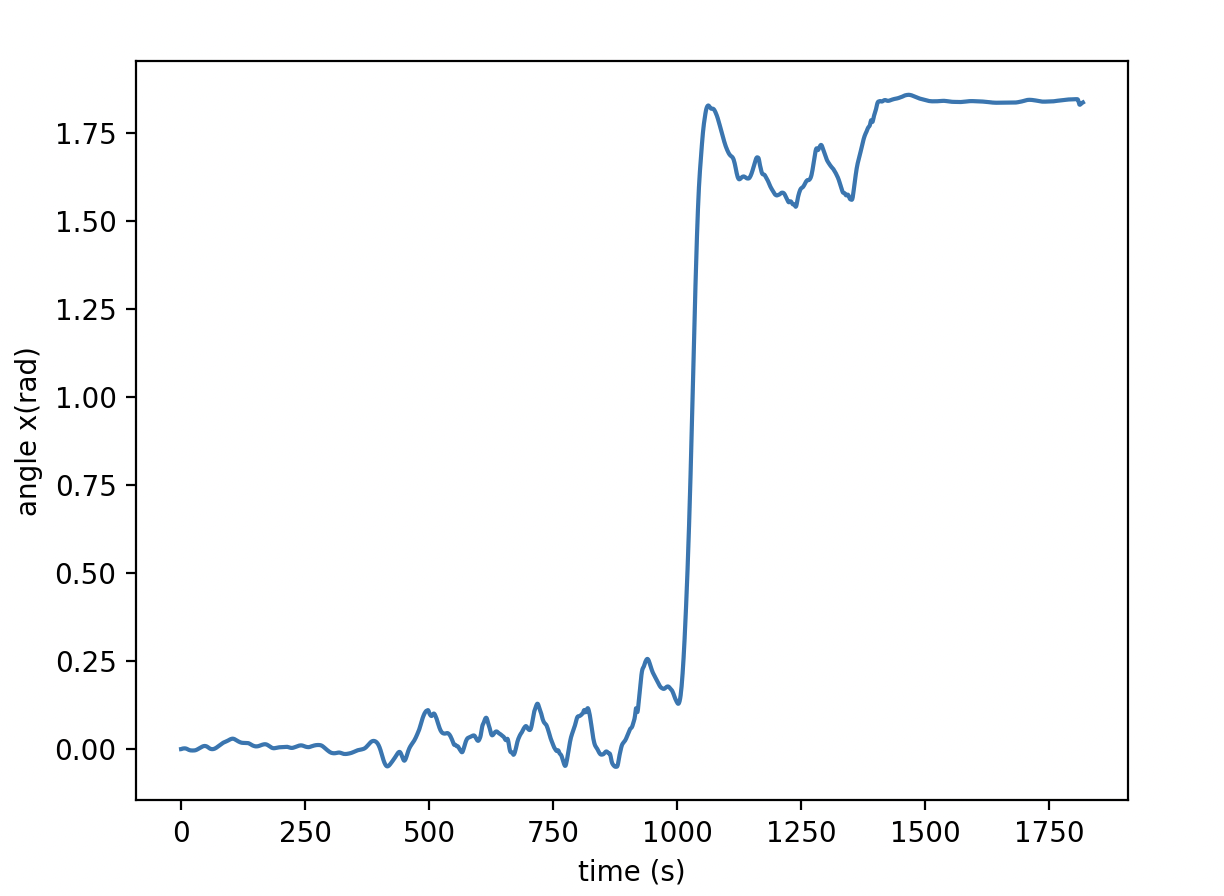
角速度を積分してx軸の角度と経過時間tのグラフを求める．
今回は定積分で求めるが台形積分などを用いた方がより正確なものになる可能性がある．
angle_x.py
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Constants
SAMPLING_FREQ = 100 # Hz
DT = 1 / SAMPLING_FREQ
if __name__ == '__main__':
gyro_data = pd.read_csv('./data/Gyroscope.csv')
angle_data = np.cumsum(gyro_data * DT)
# Plot angle data
plt.xlabel('time (s)')
plt.ylabel('angle x(rad)')
plt.plot(angle_data['x'])
plt.show()
歩行時の角度を求める
ここでは歩いた時の角度を求める．そのためにはピーク時の角度の情報が必要である．
アプリケーションで加速度センサとジャイロスコープを同時に使用してデータを取得する際,データの時間が微妙にずれることがある．そのためCSVデータのインデックスが同じであっても，実際には異なる時間を示す場合がある．この問題に対処するために加速度のピーク時の時間（t）と角度の時間（t）を小数点以下第二位で四捨五入する．その後四捨五入された時間が一致するデータポイントを探し，その時点での角度を取得する．
main.py
import numpy as np
import pandas as pd
from scipy import signal
# Constants
ACC_FILE_PATH = './data/Accelerometer.csv'
GYRO_FILE_PATH = './data/Gyroscope.csv'
SAMPLING_FREQ = 100 # Hz
DT = 1 / SAMPLING_FREQ
def search_peek_time(file_path):
df = pd.read_csv(file_path)
df['norm'] = (df['x']**2 + df['y']**2 + df['z']**2)**0.5
df['low_norm'] = df['norm'].rolling(window=10).mean()
# ピークを検出
peek, _ = signal.find_peaks(df['low_norm'], height=12)
## peekのtを取得
peek_t = df['t'][peek]
return np.round(peek_t,2)
if __name__ == '__main__':
gyro_data = pd.read_csv(GYRO_FILE_PATH)
# 't'列を除外したデータを取得
gyro_data_no_t = gyro_data.drop(columns=['t'])
# 'x', 'y', 'z'列のみを積分
angle_data_no_t = np.cumsum(gyro_data_no_t * DT)
# 積分したデータに't'列を結合
angle_data = pd.concat([gyro_data['t'], angle_data_no_t], axis=1)
angle_data['rounded_t'] = np.round(angle_data['t'], 2)
# search_peek_time()のkeysを取得
peek_t_values = search_peek_time(ACC_FILE_PATH).values
angle_data_peek = angle_data[angle_data['rounded_t'].isin(peek_t_values)]
angle_data_peek_x = angle_data_peek['x']
print(angle_data_peek)
出力結果(ピーク値の角度データ)
t x y z rounded_t
503 5.076937 0.094959 -0.111002 -0.011993 5.08
558 5.631134 0.007126 -0.051790 0.009836 5.63
609 6.145030 0.071138 -0.096628 0.037697 6.15
661 6.668999 0.009766 -0.053564 -0.040562 6.67
715 7.213116 0.118669 -0.085296 0.028185 7.21
764 7.706856 -0.014282 -0.063530 -0.001579 7.71
818 8.250977 0.111747 -0.057000 0.059152 8.25
870 8.774946 -0.043131 0.015567 -0.043714 8.77
923 9.308991 0.141047 0.004879 0.020186 9.31
1169 11.787768 1.645838 -0.263107 0.351863 11.79
1229 12.392348 1.555281 -0.147883 0.359222 12.39
1285 12.956623 1.703267 -0.235061 0.398748 12.96
1343 13.541050 1.574113 -0.079940 0.353160 13.54
1397 14.085172 1.798909 -0.103649 0.400171 14.09
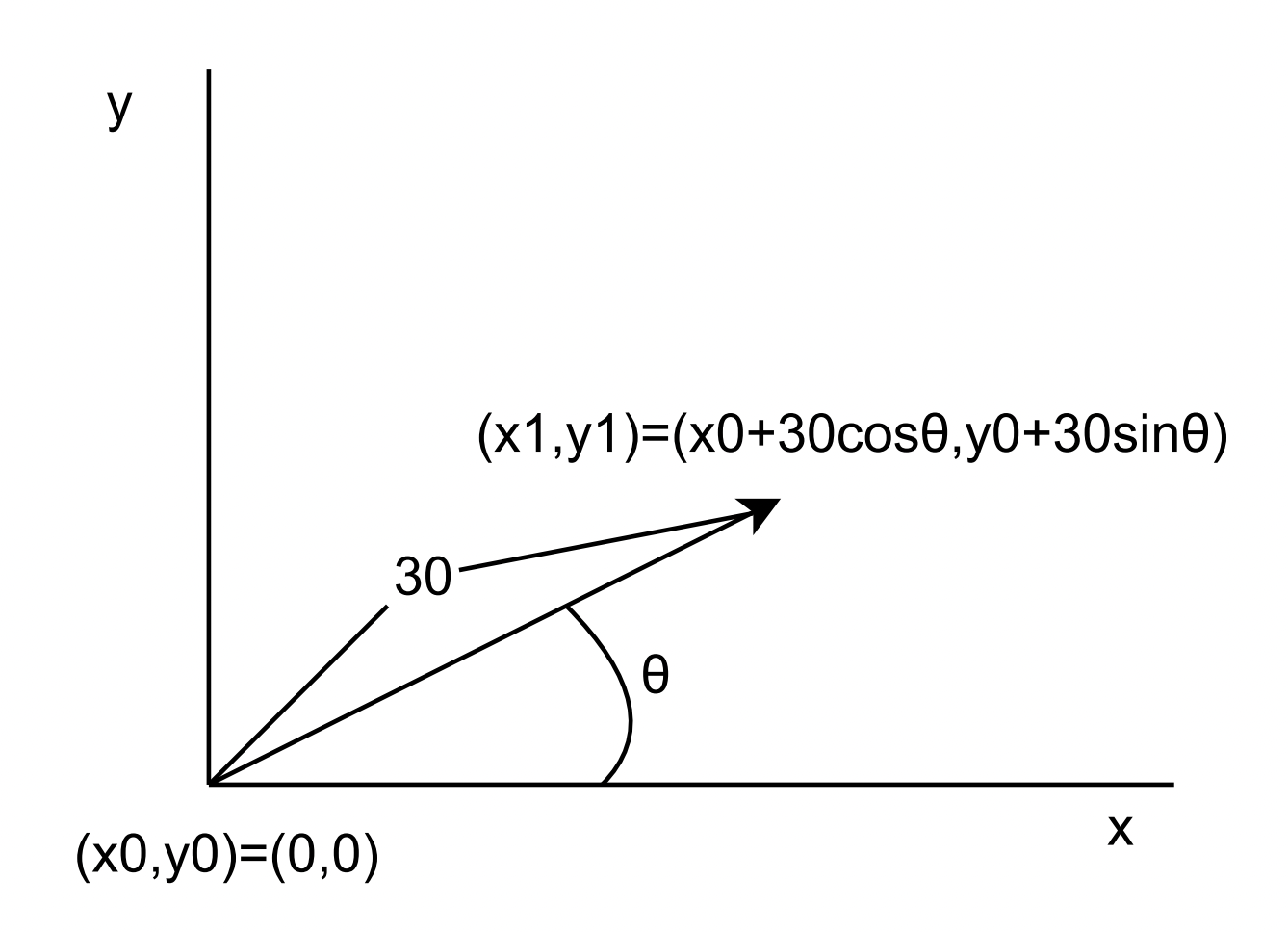
ノルムと角度データからx,y座標で表現
歩幅を設定する必要がある．今回は1歩30cmと設定する．
この歩幅がx,y座標におけるノルムに該当する．
進行方向とノルムが分かればx,y座標に歩行軌跡を表せる.
main.py
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import signal
# Constants
ACC_FILE_PATH = './data/Accelerometer.csv'
GYRO_FILE_PATH = './data/Gyroscope.csv'
SAMPLING_FREQ = 100 # Hz
DT = 1 / SAMPLING_FREQ
STEP_LENGTH = 30 # cm
def search_peek_time(file_path):
df = pd.read_csv(file_path)
df['norm'] = (df['x']**2 + df['y']**2 + df['z']**2)**0.5
df['low_norm'] = df['norm'].rolling(window=10).mean()
# ピークを検出
peek, _ = signal.find_peaks(df['low_norm'], height=12)
## peekのtを取得
peek_t = df['t'][peek]
return np.round(peek_t,2)
if __name__ == '__main__':
gyro_data = pd.read_csv(GYRO_FILE_PATH)
# 't'列を除外したデータを取得
gyro_data_no_t = gyro_data.drop(columns=['t'])
# 'x', 'y', 'z'列のみを積分
angle_data_no_t = np.cumsum(gyro_data_no_t * DT)
# 積分したデータに't'列を結合
angle_data = pd.concat([gyro_data['t'], angle_data_no_t], axis=1)
angle_data['rounded_t'] = np.round(angle_data['t'], 2)
# search_peek_time()のkeysを取得
peek_t_values = search_peek_time(ACC_FILE_PATH).values
angle_data_peek = angle_data[angle_data['rounded_t'].isin(peek_t_values)]
angle_data_peek_x = angle_data_peek['x']
x_displacement = STEP_LENGTH * np.cos(angle_data_peek_x)
y_displacement = STEP_LENGTH * np.sin(angle_data_peek_x)
x_cumulative = np.cumsum(x_displacement)
y_cumulative = np.cumsum(y_displacement)
# 初期座標(0,0)が描画されるように挿入
x_cumulative = np.insert(x_cumulative, 0, 0)
y_cumulative = np.insert(y_cumulative, 0, 0)
plt.figure()
plt.plot(x_cumulative, y_cumulative, marker='o')
x_max = max(x_cumulative)
y_max = max(y_cumulative)
#軸を揃える
plt.xlim(0,max(x_max,y_max)+10)
plt.ylim(0,max(x_max,y_max)+10)
plt.xlabel('X Displacement (cm)')
plt.ylabel('Y Displacement (cm)')
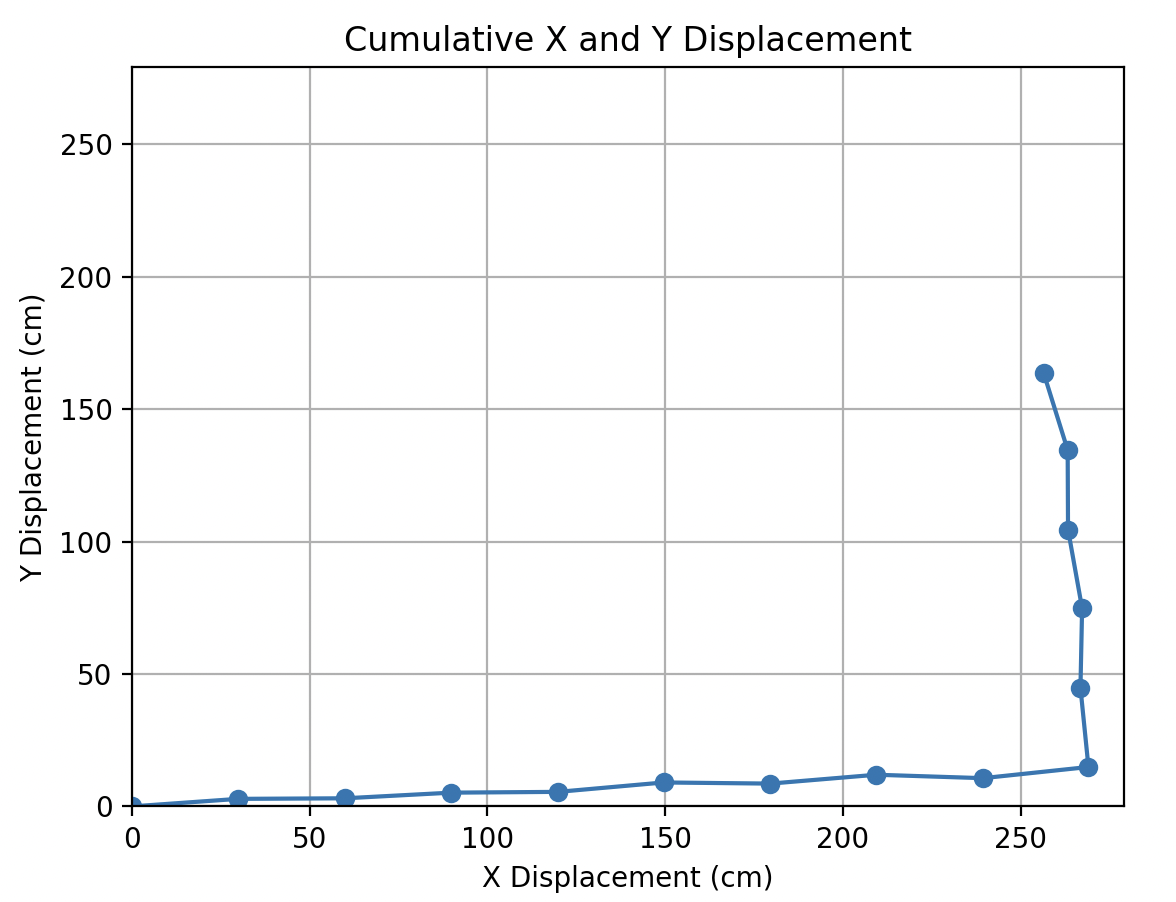
plt.title('Cumulative X and Y Displacement')
plt.grid()
plt.show()
直進する歩行データを元にプロットしたが実際には角速度が微妙に乗るため完全な直線ではない．
歩く歩数が多くなるほどこの角速度が積み重なり誤差につながるのでその場合は補正などを行い誤差を軽減する必要がある．
終わりに
今回は加速度，角速度データから歩行軌跡を描いた．
機会があればドリフトの除去や高低差があるような場合の歩行推定なども行いたい．
今回使用したセンサデータとコードはGitHubにも公開しているのでこちらも参考になるかもしれない．
Discussion