Zenn
👑

[Nim] KD木とAsymmetric Numeral Systemを使って最近傍点探索

2023/12/21に公開
Nim
#
ans
#
kdtree
tech

概要

  • 2次元K-D木
  • Asymmetric Numeral System(エンコードのみ)

をNimで書いて、多対多の最近傍点探索を行いました。

リポジトリ

https://github.com/hand-accident/kdsearch

環境

  • windows 10
  • nim 2.0.0

ただnimは素晴らしいので多分他のOSでも動くんじゃないかなと思います。

アドベントカレンダー

この記事は仙骨マウスパッドアドベントカレンダー2023に参加しています。

https://adventar.org/calendars/8562

仙骨マウスパッドって何？

動機

平面図に書かれた標高点を読み取って、3次元モデルを作りたいことがありませんか？

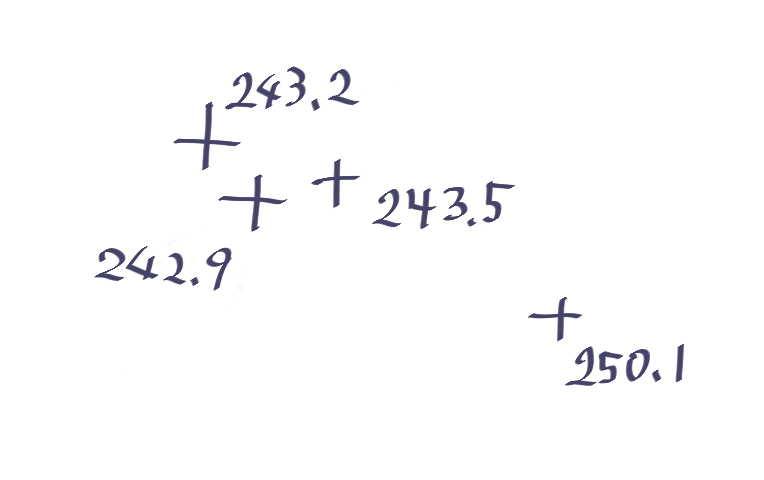
図面の一部の再現
図面の一部の再現

今はそうでなくてもいずれそのようになります。
4点くらいだったら手作業で良いのですが、残念ながらこの図面には数千個あって……

ダルいのでCADをCOMでグリグリいじってテキストの位置と内容、それから標高点マークの位置をスクレイピングしました。

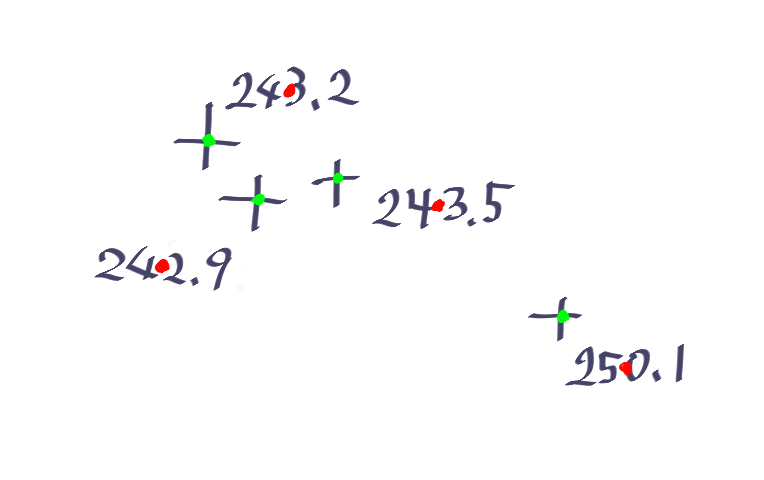
スクレイピングできた点の実際の位置
スクレイピングできた点の実際の位置

はい。印刷を前提としている図面であるので、この世の終わりのようにテキストの位置がターゲットの座標から全部ずれています。
重なってたら見づらいですからね。しかも上下左右にずれてあるので単純なオフセットではありません。

とりあえずcsvにエクスポートしたはいいものの、

texts.csv
x,y,text_z,
(以上,数千行,略),
156.0,302.9,243.2
(以下,数千行,略),
points.csv
x,y,
(以上,数千行略),
155.7,301.1,
(以下,数千行略),

この、何……？
順番もバラバラでございます。

CSVを読み込む

from std/streams import newFileStream
import std/[
  os,
  parsecsv,
  strutils,
]

type
  Coord[T] = tuple[x, y: T]

proc xy[T](x, y: T): Coord[T] =
  (x, y)

func rowToCoord(r: CsvRow): Coord[float] =
  r[0].parseFloat.xy r[1].parseFloat

proc readTextPoints(filename: string): tuple[
    points: seq[Coord[float]], heights: seq[float]
] =
  var s = filename.newFileStream fmRead
  if s == nil:
    quit("cannot open the file " & filename)
  block:
    var x: CsvParser
    defer:
      x.close
    x.open s, filename
    var strCache: seq[string]
    while x.readRow:
      let r = x.row.join""
      if r notin strCache:
        result.points &= x.row.rowToCoord
        result.heights &= x.row[2].parseFloat
        strCache &= r

proc readPoints(filename: string): seq[Coord[float]] =
  var s = filename.newFileStream fmRead
  if s == nil:
    quit("cannot open the file " & filename)
  block:
    var x: CsvParser
    defer:
      x.close
    x.open s, filename
    var strCache: seq[string]
    while x.readRow:
      let r = x.row.join""
      if r notin strCache:
        result &= x.row.rowToCoord
        strCache &= r

とりあえず書きました[1]。
DRYじゃないですね。
特にCSVを開いて閉じてするところが本質的に共通なのでくくり出したいですが出入りの型が違うから関数では……

templateがあります。

template withCsv(filename: string, body: untyped): untyped =
  var s = filename.newFileStream fmRead
  if s == nil:
    quit("cannot open the file " & filename)
  block:
    var x {.inject.}: CsvParser
    defer:
      x.close
    x.open s, filename
    body

template cachedReadLoop(filename: string, body: untyped): untyped =
  filename.withCsv:
    var strCache: seq[string]
    while x.readRow:
      let r = x.row.join""
      if r notin strCache:
        body
        strCache &= r

proc readTextPoints(filename: string): tuple[
    points: seq[Coord[float]], heights: seq[float]
] =
  filename.cachedReadLoop:
    result.points &= x.row.rowToCoord
    result.heights &= x.row[2].parseFloat

proc readPoints(filename: string): seq[Coord[float]] =
  filename.cachedReadLoop:
    result &= x.row.rowToCoord

返り値の型にuntypedを用いたtemplateはコンパイル時に型が推測されて、いい感じになります。
template内で定義されたシンボルは基本マングリングされて衛生的です[2]。
{.inject.}プラグマで明示的にスコープを貫通できます[3]。
untypedな引数を渡すと、評価を遅延させ、コードブロックを埋め込むことができます。

とりあえずやる

全探索

まずはとりあえずすべての点同士の距離を計算してそれぞれ一番近い点を探してみましょう。
y = \sqrt x は x \gt 0 で単調増加なので距離のかわりに距離の2乗で比較します。

import std/[sequtils]

proc distance2(p, q: Coord[float]): float =
  let d = (p.x - q.x).xy (p.y - q.y)
  d.x * d.x + d.y * d.y

proc main(path: tuple[texts, points: string]): seq[tuple[x, y, z: float]] =
  let
    (txts, hs) = path.texts.readTextPoints
    ps = path.points.readPoint
  
  for p in ps:
    var temp: tuple[i: int, d: float] = (-1, Inf)
    for (i, text) in txts:
      let d = p.distance2(text)
      if d < temp:
        temp = (i, d)
    result &= (p.x, p.y, hs[i])

\mathcal{O}(n^2) です。
点の数が10個とかならいいんですけど、数千あるのでちょっと日が暮れてしまいます[4]。

K-D木(K-D tree)について

大小があるデータを高速に探索するために、ただソートするだけでなく木構造に変形して取り扱うと良いことが知られています。
2分木
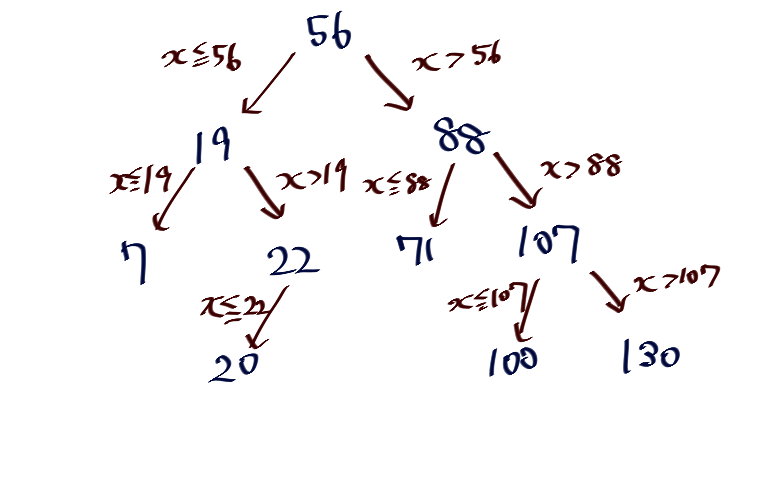
2分木(1次元K-D木)

詳しくはwikipedia

https://ja.wikipedia.org/wiki/二分木
https://en.wikipedia.org/wiki/Binary_tree

今回は2次元のデータを扱うので単純な大小比較ができません。

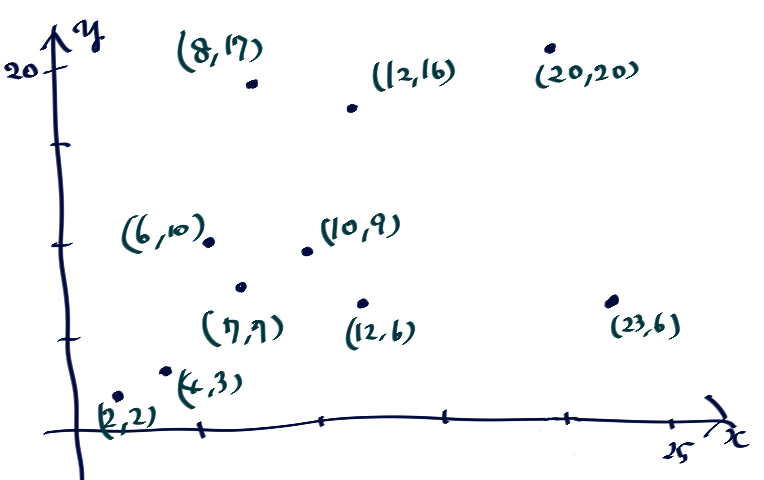
サンプルデータ
サンプルデータ

そこで、こうします。

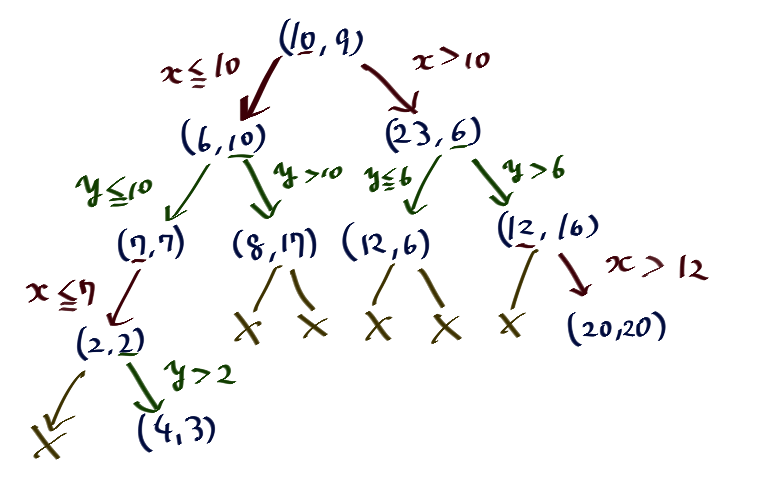
2次元K-D木
2次元K-D木

X座標とY座標を交互に分岐の指標とすることで、2分木にできます。
理論上任意次元に拡張できるのでk次元木、k-dimension tree略してkd木という名前がついています。

wikipedia kd木
https://ja.wikipedia.org/wiki/Kd木
https://en.wikipedia.org/wiki/K-d_tree

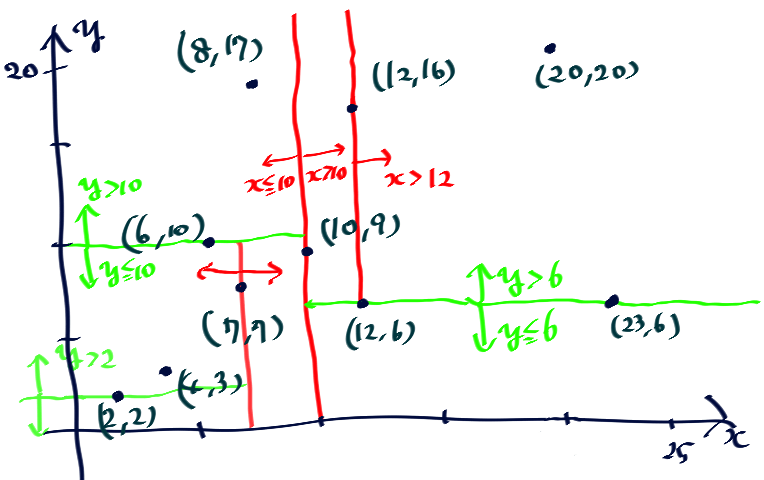
K-D木平面表現
K-D木平面表現

wikipedia バイナリ空間分割
https://ja.wikipedia.org/wiki/バイナリ空間分割
https://en.wikipedia.org/wiki/Binary_space_partitioning

おのおのの小部屋に2つ以上点が含まれなくなるまで空間を縦横に分割しているイメージです。
便宜上この小部屋をこの記事では以降areaと称します。

要素を増やしたり減らしたりするコストは普通の2分木に比べて劣りますが、今回その予定がないのでこれでいきます。

kd木での最近傍点探索

参考

https://tatsy.github.io/programming-for-beginners/cpp/kdtree/

図がめんどくさいので2次元で話をします[5]。
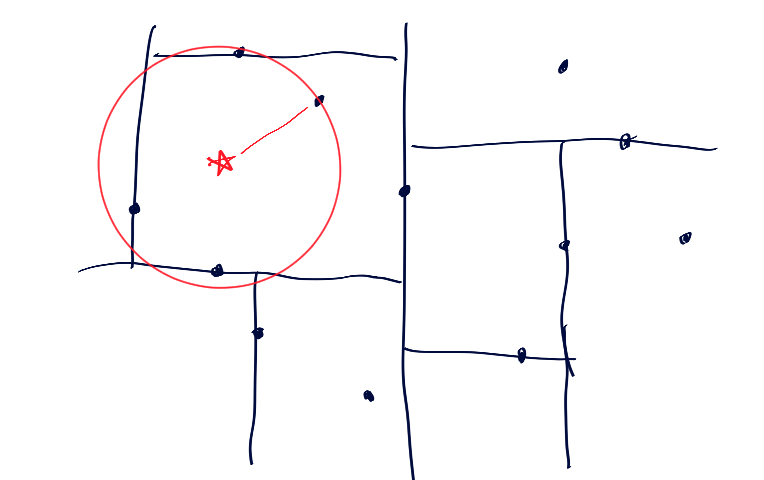
2次元kd木に変換された点群(濃藍)と、探査対象ターゲット点(赤星)、の代表点とターゲット点の距離を半径とする円(赤)
模式図-1

最近傍点を探したいターゲットの点がどのareaに入っているかどうかは、ノードの値とx/yを交互に比べながら下っていくと容易にわかります。
この記事では以降そのareaをbottomAreaと称しています。
問題は、bottomAreaの代表点が必ずしも最近傍点ではないことです。
しかし、bottomAreaの代表点とターゲットの距離を半径にもつ円が被るareaに含まれるものだけに、最近傍点候補を絞り込むことができます。

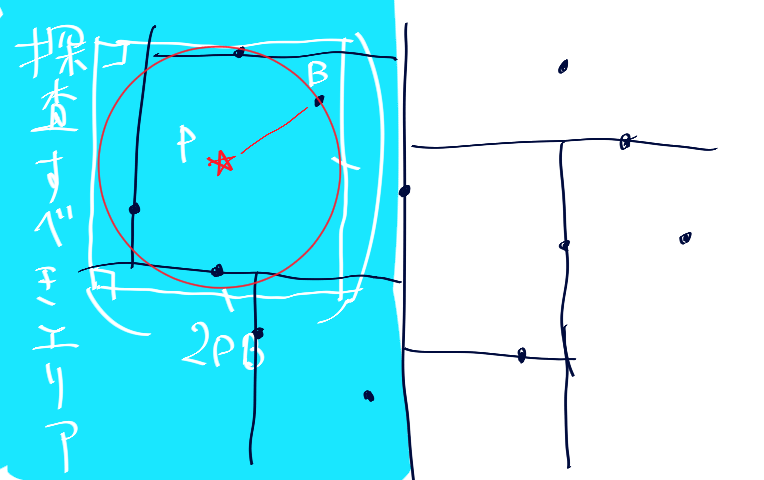
模式図-1上で、探査すべきを水色で着色
模式図-2

図中の右半分のareaに含まれる点との距離を計算する必要がないというわけですね。

円と長方形の交差判定はめんどくさいので円を正方形とみなして実装しています。四隅を比べることで判定できます。

この図だと計算が半分にしか減っていませんが、点の数が増えて密度が上がるとほとんどの点を無視できるようになります。

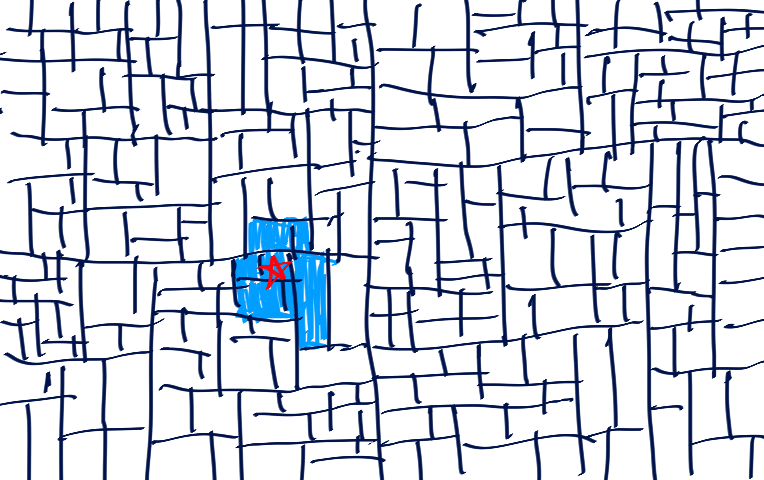
点が多い場合のイメージ
点が多い場合

とても素敵です。

kd木への変形の実装

型

標準ライブラリ

import std/[
  options,
  tables,
]

標準ライブラリから、Option型とTable型を使います。

方針

今回、

Table[NodeIndex, KDNode[T]]

kd木の本体をTableで作ることにしました。

木構造をそのままメモリ上に再現して

#[
  擬似コード
]#
type
  Node = ref object of NodeObj
    child: Node
    # ...

みたいにするべきだったのでしょうが、ポインタ周りでバグらない自信がなかったので、オブジェクトの子要素へのアクセスとまあ遜色ないだろうハッシュテーブルのキー引きで要素を取得する形にしています。

ノード間の親子関係、あるいは接続関係は後述のAsymmetric Numeral Systemで根からの経路を一意な整数へ可逆エンコードしてキーに使っているので、情報として含まれており高速に移動できます。大丈夫です。

NodeKind

type
  NodeKind* = enum
    X, Y

2分木と違って次元の数と等しい複数の指標で木を振り分けるため、
マーカーとして列挙型を用意しました。

type
  NodeIndex* = distinct int

テーブルのキーとして用いる、可逆エンコードされた経路情報です。
普通の整数型と混ざらないようにdistinctキーワードで異化しています。intと足し算しようとするとコンパイルエラーになります。

MoveKind

type
  MoveKind* = enum
    Lower, Higher

子要素が、ノードの値より大きいか小さいかを示す列挙型です。
こういうちまちましたものを定義していると抽象化にとても効きます。

Bound

type
  HasHighLow[T] = tuple[l, h: T]
  Bound*[T] = HasHighLow[Coord[T]]

下限と上限を表す総称型にCoordを差し込んで、長方形の形をした範囲を表す型を作りました。
各areaの範囲がわかっていると探索の際に便利なのでkd木の生成時点で一緒に計算します。

KDNode

type
  KDNode*[T] = tuple[kind: NodeKind, value: Coord[T], boundary: Bound[T]]

tableの値となる、ノードの情報です。

その他

type
  DirectedIndex* = tuple[x: NodeIndex, s: MoveKind]

  ConstructionProps*[T] = tuple[
    pivot: Coord[T],
    path: seq[MoveKind],
    bound: Bound[T],
    kind: NodeKind]
  SeivingProgress*[T] = tuple[
    path: seq[MoveKind],
    remains: seq[Coord[T]],
    bound: Bound[T],
    kind: NodeKind]

  PathNode*[T] = tuple[path: seq[MoveKind], node: KDNode[T]]
  MovesPathNodes*[T] = tuple[
    moves: seq[MoveKind],
    pathNodes: seq[PathNode[T]]]

  GetChild* = proc(arg: DirectedIndex): Option[NodeIndex] {.closure.}

あとは計算途中に使う混みごみした型です。エイリアスであるものはインラインで書いても良いのですが、煩雑になったので分離しました。
GetChildはMoveKindとNodeIndexのタプルを引数にとって、子ノードのNodeIndexを返す関数です。メモ化してあちこちにこの型の関数オブジェクトを引きずり回します。

type
  Arithable* = concept x, type T
    cmp(x, x) is int
    x + x is T
    x - x is T
    x * x is T

このあとTにfloatでもintでもないものをぶち込む予定なので、閉じた加減乗算と大小比較のできるトレイト境界というかジェネリクス制約としてArithableを定義しています[6]。

kd木の表現は

tuple[tree: Table[NodeIndex, KDNode[T]], getChild: GetChild]

を用います。

Asymmetric Numeral System について

wikipedia(英語)
https://en.wikipedia.org/wiki/Asymmetric_numeral_systems

参考
https://qiita.com/hon_no_mushi/items/ec3da2662fe83ab7207d

asymmetric numeral system(ANS)は、2014年にJarek Dudaによって発表された一連のエントロピー符号で、身近なところだとZstandardなどに使われています。
「非対称数系」という和訳があるみたいですが、見る限りそんなに浸透してなさそうです[7]。

ANSにも複数変種があって、今回はそのうちもっとも簡単なuniform binary variant(uABS)を使っています。

0と1でもAとBでもなんでもいいんですけど、その列を一つの整数に変換する仕組みで、原理の説明はしませんが、似たような符号化方式のハフマン符号やRange Encodingに比べて圧縮効率がよく高速だそうです。

今回ルートからの経路をseq[MoveKind]で表しており、その中身はLowerかHigherです。

kd木は2分木で、すなわち3つ以上に分岐するノードがないので、この2つの記号列で一意にノードの場所を決定できます。

実装

const ROOTINDEX* = 1.NodeIndex

const PRECISION = 24

func spread(i: SomeInteger): int =
  (i shl PRECISION).int

const NORMALIZER = 1.spread

func spreadCeilDiv(a, b: SomeInteger): int =
  a.uint64.spread.ceilDiv(b.int)

func spreadFloorDiv(a, b: SomeInteger): int =
  a.uint64.spread.floorDiv(b.int)

proc `==`*(x, y: NodeIndex): bool {.borrow.}
proc `$`*(x: NodeIndex): string = fmt":{x.int:X}:"

proc memoize[A, B](f: proc(a: A): B): proc(a: A): B =
  ## Returns a memoized version of the given procedure.
  ## from https://github.com/andreaferretti/memo/blob/master/memo.nim
  var cache = initTable[A, B]()

  result = proc(a: A): B =
    if cache.hasKey(a):
      result = cache[a]
    else:
      result = f(a)
      cache[a] = result

proc genNextIndex(p: int): proc(arg: DirectedIndex): NodeIndex =
  return memoize do (arg: DirectedIndex) -> NodeIndex:
    let (x, s) = arg
    case s:
    of Lower:
      ((x.int + 1).spreadCeilDiv(p) - 1).NodeIndex
    else:
      x.int.spreadFloorDiv(NORMALIZER - p).NodeIndex

proc genEncoding(
      nextIndex: proc(arg: DirectedIndex): NodeIndex
    ): proc(ss: seq[MoveKind]): NodeIndex =
  return proc(ss: seq[MoveKind]): NodeIndex =
    ss.foldl (a, b).nextIndex, ROOTINDEX

proc genParams(ss: seq[MoveKind]): int =
  ss.countIt(it == Lower).spreadFloorDiv(ss.len)

uABSにおいて2つの記号が同じ頻度で出現するとき、符号はハフマン符号のものと同じになります。ハフマン符号以上の圧縮になるには、出現頻度が偏っていることが必要です。

2分木という性質上、偏りが少ないほうが探索回数が減って好ましいのですが、挿入や回転にそこそこコストを要求するkd木において完全な平衡を取るのは重いので、偏ります。

genParamsは全てのノードの経路をflattenしたseq[MoveKind]を引数にとって出現確率を計算します。
エンコード過程で出てくるdivModをビット演算にするために、出現確率を分母が2の累乗になるように近似しています。
具体的には 2^{-24}\cdot n\quad(n\in \mathbb{N},0\leqq n\leqq2^{24}) です。

一文字ずつエンコードすることができるので、特定の与ノードの子を求めることが自然にできます。

デコードも同じように一文字ずつできるので子ノードから親ノードをたどることができますが、リファクタリングしていたらデコード部分が消えました。木の構築と探索をエンコードのみで行っています。

メモ化のコードは https://github.com/andreaferretti/memo/blob/master/memo.nim のものと同一です。

値の分別

proc getValue[T](c: Coord[T], kind: NodeKind): T =
  case kind
  of X:
    c.x
  of Y:
    c.y

proc medianOfMedians[T: Arithable](ss: seq[T]): T =
  proc select(s: seq[T]): T =
    if s.len == 1:
      s[0]
    elif s.len == 2:
      s[1]
    elif s.len mod 2 == 0:
      (s.sorted)[s.len div 2]
    else:
      (s.sorted)[s.len div 2 + 1]
  var temp = ss
  while temp.len > 5:
    temp = ss.distribute(5).mapIt(it.select)
  temp.select

proc sieve[T: Arithable](cs: seq[Coord[T]], kind: NodeKind): tuple[
    l, h: seq[Coord[T]],
    pivot: Coord[T]] =
  let
    pivotValue = cs.mapIt(it.getValue(kind)).medianOfMedians
    pivot = cs.filterIt(it.getValue(kind) == pivotValue)[0]
    pivotIndex = cs.find pivot

  result.pivot = pivot
  for i, c in cs:
    if likely(i != pivotIndex):
      if c.getValue(kind) > pivotValue:
        result.h &= c
      else:
        result.l &= c

proc tighten[T](bound: Bound[T], value: Coord[T], kind: NodeKind,
    move: MoveKind): Bound[T] =
  case kind
    of X:
      case move
      of Lower:
        (bound.l, (value.x, bound.h.y))
      else:
        ((value.x, bound.l.y), bound.h)
    of Y:
      case move
      of Lower:
        (bound.l, (bound.h.x, value.y))
      else:
        ((bound.l.x, value.y), bound.h)

sieveは与えられた座標csから、指標の軸(NodeKind)についての概ね中央値(pivot)を取り出して、それより低い/高い座標2つのseqに分類します。
tightenは現在の値の範囲をpivotとNodeKindとMoveKindで狭めてあたらしい範囲を取得します。
c.xとかc.yとか直接書いてると絶対どこかで間違うのでgetValueを定義しています。

中央値の中央値

中央値っぽい値を高速に取得するアルゴリズムとして、「中央値の中央値(median of medians)」を使っています。

wikipedia
https://ja.wikipedia.org/wiki/中央値の中央値
https://en.wikipedia.org/wiki/Median_of_medians

四分範囲のどこかの値を \mathcal{O}(n) で取ってくるので、単にソートして正確な中央値を求めるよりも若干速いです。

State

HaskellのStateにあたるものを書きました。

参考
https://qiita.com/7shi/items/2e9bff5d88302de1a9e9

「状態付き計算」という言葉でよく語られるように、S -> (S, T)という型の関数をラップしたものです。
その性質の良さを活かして後述のDFSの実装の際にいい感じに手続きをカプセル化・合成できるかなと思ったのですがあまり乗りこなせていません。

type
  StateInner*[S, T] = tuple[state: S, value: T]
  State*[S, T] = object
    runS*: proc(initS: S): StateInner[S, T]

proc initState*[S, T](f: S -> StateInner[S, T]): State[S, T] =
  result.runS = f

proc getState*[T](): State[T, T] =
  initState((t: T) => (t, t))

proc putState*[T](t: T): State[T, Unit] =
  initState((_: T) => (state: t, value: unit))

proc runState*[S, T](st: State[S, T], s: S): StateInner[S, T] =
  (st.runS)(s)

proc evalState*[S, T](st: State[S, T], s: S): T =
  st.runState(s).value

proc execState*[S, T](st: State[S, T], s: S): S =
  st.runState(s).state

Nimのタプルはフィールドに名前をつけられるので、順番を間違えるのを減らせます。
evalStateとexecStateは本家と違って正格評価になってしまったので遅いです。

DFSの実装(テンプレート)

個人的に深さ優先探索(DFS)を書くのがとても苦手で、whileループするにも再帰するにも停止条件やスタックからの取り出しをミスってすぐPCを落としてしまいます。なのでその部分だけテンプレートに切り出しました。

proc safeHead*[T](s: seq[T]): Option[T] =
  if s.len != 0:
    return s[0].some

proc getTail*[T](s: seq[T]): seq[T] =
  if s.len >= 2:
    return s[1..^1]

proc safeHeadTail*[T](s: seq[T]): tuple[head: Option[T], tail: seq[T]] =
  (s.safeHead, s.getTail)

template dfsLoopWith*[S, T](
    step: State[seq[S], T],
    initial: S,
    RetType: typedesc,
    body: untyped): untyped =
  block:
    var
      loopResult {.inject.}: RetType
      stack: seq[S]
      current: Option[S]

    current = initial.option
    while current.isSome:
      let
        sv: tuple[state: seq[S], value: T] = step.runState @[current.unsafeGet]
        descendants = sv.state
        stepResult {.inject.} = sv.value
      if descendants.len > 0:
        stack = descendants & stack
      body
      (current, stack) = stack.safeHeadTail
    loopResult

template dfsLoop*[S, T](
    step: State[seq[S], T],
    initial: S,
    body: untyped): untyped =
  step.dfsLoopWith(initial, seq[T]):
    body

proc prepareDfsState*[S, T](
    calcDfsStep: proc(h: S): StateInner[seq[S], T]): State[seq[S], T] =
  initState do (s: seq[S]) -> StateInner[seq[S], T]:
    calcDfsStep(s[0])

stepは先程説明したStateです。
stepの名前の通りループ中の1ステップを表す引数です。
runStateによってスタックから取り出された値を要素数1のseqで受け取ってスタックに追加する値(0個以上)と計算結果を返します。
runStateの引数がスタック全体ではないことに混乱しないように、S -> (seq[S], T)を受け取ってState[seq[S], T]を返すperpareDfsStateを書きました。

また、DFSによって常にseqを得たいわけではない(遅延評価ではないのでループと同時にflattenしたりfoldしたり副作用を起こしたりして最適化したい)ので、dfsLoopWith[S, T](step: State[seq[S], T], initial: S, RetType: typedesc, body: untyped)という形式を用意し、stepの返り値と違う型を明示的に返せるようにしています。
bodyのところに呼び出し側のコードが展開されますが、step.runStateのvalue側の実行結果であるstepResult: Tと、返り値を格納するloopResult: RetTypeしか露出させないことで、呼び出し側でスタックやループ機構を生で触れないようにしました。私は私を信用していません。

木の構築

proc other(kind: NodeKind): NodeKind =
  case kind
  of X: Y
  of Y: X

proc nextMove(ms: seq[MoveKind], m: MoveKind): seq[MoveKind] =
  result = ms
  result &= m

proc recentMove(ms: seq[MoveKind]): Option[MoveKind] =
  if ms.len > 0:
    ms[^1].some
  else:
    MoveKind.none

汎用関数です。NodeIndexにエンコードする前のseq[MoveKind]に対するMoveKindの追加(nextMove)と、上のノードからの関係の取得(recentMove)は直感的に行えます。

proc nextSeivingProgress[T](
    p: SeivingProgress[T], m: MoveKind, pivot: Coord[T]): SeivingProgress[T] =
  let (path, remains, bound, kind) = p
  (path.nextMove(m), remains, bound.tighten(pivot, kind, m), kind.other)

proc toPathNode[T](props: ConstructionProps[T]): PathNode[T] =
  let
    (pivot, path, bound, kind) = props
    lastMove = path.recentMove
    optionalBound = lastMove.map(it => bound.tighten(pivot, kind, it))
    newBound: Bound[T] = optionalBound.get(bound)
  (path, (kind, pivot, newBound))

proc createPathNodes[T: Arithable](cs: seq[Coord[T]], initialBound: Bound[
    T]): MovesPathNodes[T] =
  type
    TheState = State[seq[SeivingProgress[T]], ConstructionProps[T]]
    TheSI = StateInner[seq[SeivingProgress[T]], ConstructionProps[T]]
  let
    initialState: SeivingProgress[T] = (@[], cs, initialBound, X)
    step: TheState = prepareDfsState do (h: SeivingProgress[T]) -> TheSI:
      let
        (path, remains, bound, kind) = h
        (lowers, highers, pivot) = remains.sieve kind
      if highers.len > 0:
        result.state &= (path, highers, bound, kind).nextSeivingProgress(Higher, pivot)
      if lowers.len > 0:
        result.state &= (path, lowers, bound, kind).nextSeivingProgress(Lower, pivot)
      result.value = (pivot, path, bound, kind)

  step.dfsLoopWith(initialState, MovesPathNodes[T]):
    for m in stepResult.path:
      loopResult.moves &= m
    loopResult.pathNodes &= stepResult.toPathNode

createPathNodes は 全体の範囲を指定して座標一覧seq[Coord[T]]をMovesPathNodes[T]に変換します。
大雑把な流れとして、createPathNodes中のstepは(@[], cs, initialBound, X)を初期値として、スタック上の残りの座標remainをseiveでpivot,lowers, highersの3つに分割し、lowers, highersがそれぞれ存在する場合はスタックに次の篩いに用いる引数を載せます。
いくつか気持ちの図があります。
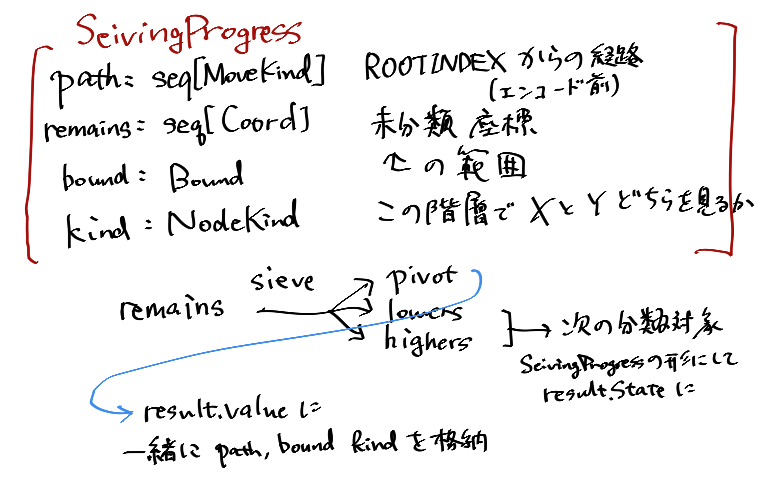
createPathNodes.step.runstateの気持ちの図(型について)
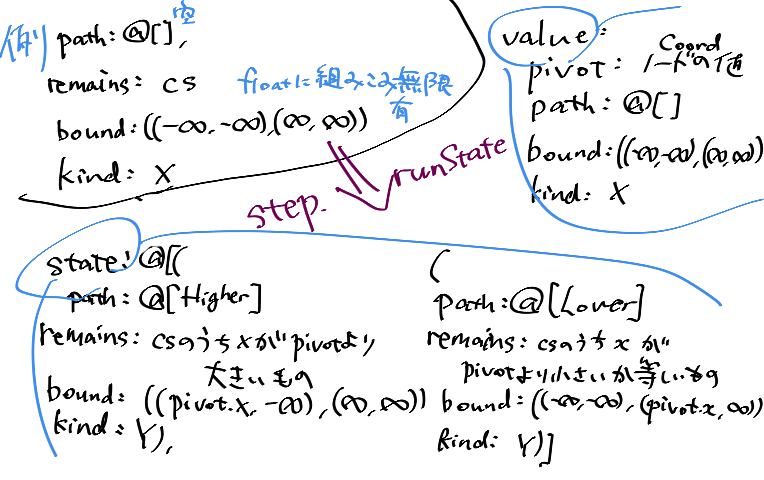
createPathNodes.step.runstateの気持ちの図(初期値に対して実行した例)

このstepをDFSに乗せて、適切に整形して返しています。
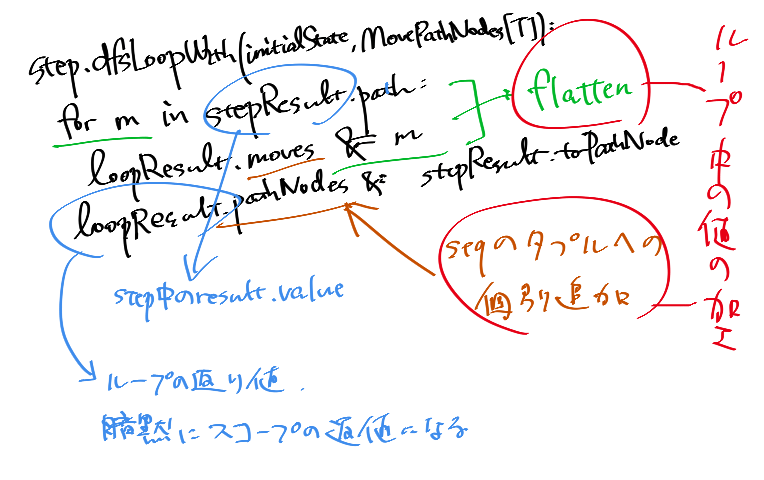
dfsLoopWith呼び出し側の気持ちの図

一度のループでできることをとりあえず全部やって計算回数を減らそうとしているのでかなり色々なことが起こってしまっていて可読性が犠牲になっていますが、見た目に関してせめて最悪を避けようという努力を汲み取っていただけると幸いです。

再掲ですが

type
  KDNode*[T] = tuple[kind: NodeKind, value: Coord[T], boundary: Bound[T]]
  PathNode*[T] = tuple[path: seq[MoveKind], node: KDNode[T]]
  MovesPathNodes*[T] = tuple[
    moves: seq[MoveKind],
    pathNodes: seq[PathNode[T]]]

という定義をしているため、path: seq[MoveKind]で表された経路情報をuANSを用いてNodeIndexに変換することでseq[(NodeIndex, KDNode[T])]が得られ、これはKD木の今回の表現形であるTable[NodeIndex, KDNode[T]]に容易に変換できます。
MovePathNodesにはついでにLowerとHigherの割合を割り出すためのseq[Movekind]が含まれています。
これをgenNextIndexに通すことでnextIndex: DirectedIndex -> NodeIndexを得ます。
nextIndexに子ノードがあるかどうかをOptionで表す機構を合成し、nilチェックとかをしなくていいgetChildが得られます。
子ノードがないときNodeIndex.none: Option[NodeIndex]が返ります。

proc toKD*[T: Arithable](
      cs: seq[Coord[T]], initialBound: Bound[T]
    ): tuple[tree: Table[NodeIndex, KDNode[T]], getChild: GetChild] =
  let
    (moves, pathNodes) = cs.createPathNodes initialBound
    param = moves.genParams
    nextIndex = genNextIndex(param)
    encoding = genEncoding(nextIndex)

  var ks: seq[NodeIndex]
  for (path, node) in pathNodes:
    let i = path.encoding
    result.tree[i] = node
    ks &= i

  result.getChild = memoize do (arg: DirectedIndex) -> Option[NodeIndex]:
    arg.nextIndex.option.filter code => code in ks

探索の実装

bottomAreaの算出

探したい点が含まれる最狭のarea、bottomAreaを求めます。

type
  GetChild* = proc(arg: DirectedIndex): Option[NodeIndex] {.closure.}
  Extract*[T] = proc(i: NodeIndex): tuple[
      v: Coord[T], k: NodeKind, value: T] {.closure.}
  BottomCacheArea*[T] = tuple[
    bottom: NodeIndex,
    cache: Table[NodeIndex, Option[T]],
    area: Bound[T]]
  SearchHelpers*[T] = tuple[
    getChild: GetChild,
    i2d: proc(i: NodeIndex): T,
    extract: Extract[T]]

ややこしめのproc型などです。
GetChildはインデックスと方向をとって子ノードがあればsome(NodeIndex), なければnone(NodeIndex)を返します。
ExtractはインデックスをとってKDNodeの中身を返します。
i2d: proc(i: NodeIndex): Tはindex to distanceの意味で、与点からtree[i]までの距離を求めます。
これらの関数はメモ化されているので、2回目以降は定数オーダーで走りますし、与点の情報を含んで生成されるので引数が少ないです。

proc neighborhoodArea[T: Arithable](d: T, c: Coord[T]): Bound[T] =
  ((c.x - d, c.y - d), (c.x + d, c.y + d))

proc catOptions[T](s: seq[Option[T]]): seq[T] =
  for o in s:
    if o.isSome:
      result &= o.unsafeGet

neighborhoodAreaは与点から上下左右dの範囲の正方形です。
この範囲と共通部分をもつareaが最近傍点をもつ候補なので、findBottomAreaの最後に返り値に添えています。

catOptionsはOptionの配列からsome要素だけを取り出してOptionを外します。
getChildで求めたOption[NodeIndex]を子ノードがあろうがなかろうがとりあえずseqに入れておいて一気に外すという処理ができます。
また@[child].catOptionsとすることで、childがsomeのとき@[child.unsafeGet], noneのとき@[]という分岐をすっきり記述できます。

proc findBottomArea[T: Arithable](
    fs: SearchHelpers[T], c: Coord[T]): BottomCacheArea[T] =
  type
    IndexedDistance = tuple[distance: T, i: NodeIndex]
    TheState = State[seq[NodeIndex], IndexedDistance]
    TheSI = StateInner[seq[NodeIndex], IndexedDistance]
  let
    (getChild, i2d, extract) = fs
    step: TheState = prepareDfsState do (i: NodeIndex) -> TheSI:
      let
        (_, kind, value) = i.extract
        d = i.i2d
        direction = block:
          if value < c.getValue(kind):
            Higher
          else:
            Lower
        child = getChild((i, direction))

      (@[child].catOptions, (d, i))

  var tempDistance = ROOTINDEX.i2d
  result = step.dfsLoopWith(ROOTINDEX, BottomCacheArea[T]):
    if stepResult.distance <= tempDistance:
      tempDistance = stepResult.distance
      loopResult.cache[stepResult.i] = tempDistance.option
      loopResult.bottom = stepResult.i
    else:
      loopResult.cache[stepResult.i] = T.none

  result.area = result.bottom.i2d.neighborhoodArea c

proc型のジェネリクスのタプルのアンパックというのnimsuggestくんが結構悲鳴を上げますがコンパイルは通ります。
メモ化してクロージャになっているので引数にして渡すしかありません。

MoveKindとNodeKind、そしてOptionの力によって、ふるい分け基準や子ノードへの移動方向や子ノードの有無にかかわらずgetChild((i, direction))で一括りに辿れます。ようやく気持ちよくなってきました。

result.cacheにはi2dで求めた距離がそのループ中で最短距離を更新したときsome、そうでない場合noneで格納されています。
i2dがメモ化されてあるのであまり必要ないかもしれません。

最近傍点を求める

proc findNearestHelper[T: Arithable](
    fs: SearchHelpers[T], bca: BottomCacheArea[T]): Coord[T] =
  type
    CoordDistance = tuple[value: Coord[T], distance: T]
    TheState = State[seq[NodeIndex], CoordDistance]
    TheSI = StateInner[seq[NodeIndex], CoordDistance]
  let
    (getChild, i2d, extract) = fs
    (bottom, cache, area) = bca
    bottomV = bottom.extract.v
    step: TheState = prepareDfsState do (i: NodeIndex) -> TheSI:
      let
        (coord, kind, value) = i.extract
        d = i.i2d
      var children: seq[Option[NodeIndex]]
      if area.h.getValue(kind) > value:
        children &= getChild((i, Higher))
      if area.l.getValue(kind) <= value:
        children &= getChild((i, Lower))

      result.state = children.catOptions
      result.value = (coord, cache.getOrDefault(i, d.option).get(d))

  var tempDistance = ROOTINDEX.i2d
  result = bottomV
  result = step.dfsLoopWith(ROOTINDEX, Coord[T]):
    if stepResult.distance < tempDistance:
      loopResult = stepResult.value
      tempDistance = stepResult.distance

findNearestHelperという名前ですが、探索の本体です。
今まで断りなく使ってきましたが、nimには「暗黙のresult」という機能があって、自分で定義しなくてもprocの中ではprocの返り値の型をしたミュータブル変数resultが使えます。またこのresultは関数の終わりに自動的にリターンされ[8]、デフォルト値で初期化されています[9]。
nimは後発の言語ということで守るべきものがまだ少ないので、変数宣言について、varが可変で、letはイミュータブルかつ再代入不可で、constはコンパイル時固定の定数ということにできています。
let中心にコードを書きつつ、varが欲しくなったタイミングで関数に切り出してresultを使う、なんというか目安というかリズムが生まれます。
それはそれとしてこの関数名はわかりにくいのでやがて直します。

与点からbottomAreaの代表点までの距離を半径にもつ円の近似正方形であるbca.areaの範囲の端を見ながら、その正方形が被っているareaのインデックスと与点までの距離を拾い上げていきます。

ループ呼び出し部ではより近い点が見つかるたびにtempDistanceとloopResultを更新しています。

proc square[T: Arithable](a: T): T =
  a * a

proc distance[T: Arithable](p, q: Coord[T]): T =
  let c = (p.x - q.x).square + (p.y - q.y).square

  when T is SomeNumber:
    c.float.sqrt
  else:
    c.sqrt

proc findNearest*[T: Arithable](
    n: tuple[tree: Table[NodeIndex, KDNode[T]], getChild: GetChild],
    c: Coord[T]): Coord[T] =
  let
    (tree, getChild) = n
    i2d = memoize do (i: NodeIndex) -> T:
      tree[i].value.distance(c)
    extract = memoize do (i: NodeIndex) -> tuple[
        v: Coord[T], k: NodeKind, value: T]:
      let
        node = tree[i]
        (v, k) = (node.value, node.kind)
        value = v.getValue k
      (v, k, value)

  let fs = (getChild, i2d, extract)

  fs.findNearestHelper fs.findBottomArea c

toKDで得られたテーブルとgetChildを取り出し、treeに対するextractと、treeと与点に対するi2dを定義してメモ化してfs: SearchHelpers[T]を作ります。

nim言語は統一関数呼び出し構文(UFCS)を採用していることで有名ですが、カッコでなくスペースで関数名と引数名を区切るとHaskellの$が入っているように右結合を起こすので、fs.findNearestHelper(fs.findBottomArea(c))と書くべきものからカッコをぶっ飛ばせます[10]。

実際の探索

実際の探索部分は人様にお見せできる状態まで掃除するためにそれぞれあと半年ずつかかるような私用ライブラリがいくつか根深くこびりついていたので[11]、一部抜粋にとどめます。

proc compoundNearest(
      t: tuple[
        tree: Table[NodeIndex, KDNode[IndexedFloat]],
        getChild: GetChild],
      c: Coord[IndexedFloat],
      heights: seq[float]
    ): tuple[x, y, z: float] =
  c.get.addHeight(heights[t.findNearest(c).getIndex])

proc execKdSearch*(path: tuple[base, targetHeight, output: string]) =
  var
    pts, txts: seq[Coord[IndexedFloat]]
    hs: seq[float]

  path.targetHeight.indexedCachedReadLoop:
    txts &= i.th x.row.rowToCoord
    hs &= x.row[2].parseFloat

  path.base.indexedCachedReadLoop:
    pts &= i.th x.row.rowToCoord

  let t = txts.toKD ZEROBOUND

  pts.mapIt(t.compoundNearest(it, hs)).seqToCsv(path.output)

おわりに

記事にしようと思ってから書いたコードではなかったため、掃除や解読に時間がかかりました。
増築とリファクタを繰り返してもはや書き捨てのスクリプトの文量ではなくなってしまっているので、自覚をもって再リファクタしようと思います。
テック系の記事を書くのが初めてで、またnimが比較的マイナー言語ということもあって、想定読者が書いている途中でブレまくるなどお見苦しい点もモリモリあると思いますが、あまりに目に余る箇所等ございましたらコメントでご指摘等頂けると幸いです。

脚注

  1. 今見直してたらstd/strutilsのparseFloatが例外を投げますね。
    std/optionsにせっかくOption型があるので次からは使います。 ↩︎

  2. template内の、type, var, let, constで宣言されたシンボルはデフォルトでマングリングされ、proc, iterator, converter, template, macroで宣言されたシンボルはデフォルトでマングリングされません。 ↩︎

  3. 反対に、{.gensym.}プラグマで明示的にマングリングできます。 ↩︎

  4. ゴリ押しでここで完成とするのが正解だった説はあります。10000はなかったので1億回距離を求めたら終わります。パワー。 ↩︎

  5. 2次元の場合円と長方形ですが、3次元の場合球と直方体、k次元の場合超球と超矩形になります。 ↩︎

  6. 多分もっといい名前がありますが、加法の可換性や分配律が壊れるような型を使うため、少なくとも順序可換環ではありません。 ↩︎

  7. 入力に対して非対称に繰り上がる数字列という「記数法」のニュアンスが失われるのでnumeralを"数"と訳すことに対して思うところがあるなどあります。 ↩︎

  8. さらに関数の最後のstatementが文でなく式であるときresult = が自動挿入されます。 ↩︎

  9. その型にデフォルト値が定義されている場合のみ ↩︎

  10. 好き嫌いがわかれる書き方なので、スタイルガイドによっては非推奨となっています。 ↩︎

  11. そしてアドベントカレンダーの担当日付をこれ以上延期させてもらうわけにも行かないので ↩︎

Discussion