🫣

【記事紹介】ベイジアンA/Bテストはpeekingの影響を受けないのか?

に公開
Python
ベイズ統計
A/B テスト
tech

はじめに

ベイジアンABテストについて調べ物をしている時に、興味深い記事を見つけました。

http://varianceexplained.org/r/bayesian-ab-testing/

ベイジアンABテストについてインターネットで調べると、「頻度論的な仮説検定（NHST）よりも便利で優れている！」というポジティブな記事が多く散見されます。そして、ベイズ統計を用いるメリットとして「途中で結果を確認して意思決定を行ってもよい（peekingしてもよい）」という内容が挙げられていることがあります。

これに対し、上の記事では「ベイジアンABであれば途中結果の覗き見(peeking)による影響を受けない」というメリットは少し誇張されているぞ、ということを複数のシミュレーションを通じて検証しています。

本稿では、記事内のシミュレーションをPythonで実装しながら記事の内容を自分なりに噛み砕いてみました。

サマリ

  • NHSTでは結果のpeekingによって偽陽性(第一種の過誤、TypeIエラー)が増加する。
  • 期待損失を指標としたベイズ法を用いた場合でも、peekingにより偽陽性が増加する。
    • ただし、peekingの有無に依らず、設定した閾値以上の損失が発生することはない。

peekingによる影響 - NHST

偽陽性への影響

まず初めに、NHSTでpeekingを行うと偽陽性が上がる様子をシミュレーションを通じて説明しています。

導入として、シミュレーションで利用するデータセットの説明です。
1日あたり10,000のインプレッションを獲得するWebサービスで、CTRの向上を目的とした20日間のABテストを実施することを想定します。2群のCTRは0.1%で同一の値であり、帰無仮説が成立している状況を想定しています。

peekingなしの場合は20日間全てのデータを使って有意差検定を行いますが、peekingありの場合は毎日有意差検定を行い、p値が有意水準を下回った時点でテストを終了します。

これを100回行い、有意になった回数（割合）を計算します。今回は帰無仮説が成立している状況を想定しているため、算出される割合は有意水準と等しくなるはずです。

以下にシミュレーションの結果を掲載します。これはABテスト期間（20日間）のp値の時系列推移を可視化したものです。赤線は有意と判定されたもの、黒線は有意と判断されなかったものとなります。

100回のシミュレーションのうち、peekingなしの場合は6回有意差がついており想定通りの挙動を示していますが、peekingありの場合は22回有意差がついてしまっています。peekingにより偽陽性が約4倍になってしまっています。

このようにpeekingによって偽陽性が上昇してしまうため、NHSTを用いる場合には、有意水準・検出力・効果量・サンプルサイズを事前に決定し、決められた期間データを収集してテスト終了後に1度だけ検定する必要があります。

peekingによる影響 - ベイズ

期待損失

ここからはベイズ法を用いたシミュレーションを行います。
NHSTでは意思決定の指標としてp値を用いられることがほとんどですが、ベイズではいくつかの指標を用いることが出来ます。
この記事では、期待損失を採用しています。まず初めにこちらについて簡単に説明します。

期待損失とは、もし新しいバージョンBに切り替えたとして、実際にはBがAより悪かった場合に平均してどれくらいの損をする可能性があるかを示す数値です。得られたデータからパラメータの事後分布を推定し、この事後分布から算出される期待損失が、あらかじめ設定した閾値を下回ったらBに切り替える、というルールになります。この閾値は、誤った選択をした場合に許容できる損失の上限を表します。

A, B群の真のCTRをそれぞれ \alpha, \beta とすると、新たなB群を採用する損失 L と期待損失 E[L] は以下のように書けます。

L(\alpha, \beta) = max(\alpha - \beta, 0) \\ E[L] = \int_{A} \int_{B} L(\alpha, \beta) f(\alpha, \beta) d\alpha d\beta

CTRのようなベータ分布の場合、解析的に期待損失を求めることが出来ますが、今回は簡単のためパラメータの事後分布から乱数生成をして算出を行います。（元記事の筆者は、以下の記事を参考に解析的に算出しているようでした）

https://www.chrisstucchio.com/blog/2014/bayesian_ab_decision_rule.html

https://www.evanmiller.org/bayesian-ab-testing.html

偽陽性への影響

以上を踏まえ、期待損失を指標としたベイズ法を用いる際にpeekingによる偽陽性への影響をシミュレーションで調べます。

1日あたり10,000のインプレッションを獲得するWebサービスで、CTRの向上を目的とした20日間のABテストを実施することを想定します。A群のCTRは0.10%、新しく導入したいB群のCTRは0.09%という状況を想定します。またCTRの事前分布はそれぞれ Beta(10, 990) と仮定しています。（あえて誤った事前分布の設定を想定しているようです）

peekingなしの場合は20日間全てのデータを使って期待損失を計算しますが、peekingありの場合は毎日期待損失を計算し、期待損失が閾値を下回った時点でテストを終了します。閾値は 10^{-5}(Bを選択すると10%の確率でCTRが悪化し、悪化した際には平均的に0.01%下がる = 0.1 * 0.0001)としています。

これを100回行い、閾値を下回った回数（割合）を計算します。

以下にシミュレーションの結果を掲載します。これはABテスト期間（20日間）でBを選択した場合の期待損失の時系列推移を可視化したものです。赤線は閾値を下回ったもの、黒線は閾値を下回らなかったものとなります。

100回のシミュレーションのうち、peekingなしのケースでは3回有意と判定されていますが、peekingを行った場合は13回有意と判定されています。こちらもNHSTと同様にpeekingにより偽陽性が約4倍になってしまいます。

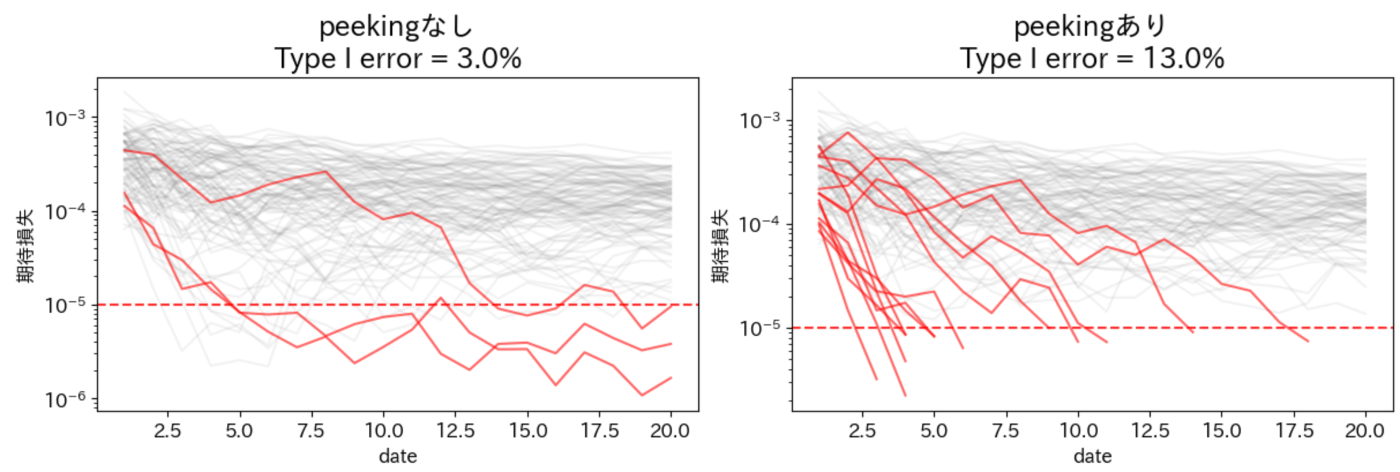
また、これは閾値に依らない傾向であることも分かります。

なぜこのような結果になるのか。答えはシンプルで、そもそも期待損失を用いた手法では偽陽性を守るという約束をしていないからと述べられています。では期待損失を用いるメリットは何なのでしょうか?

期待損失への影響

次に、2群の真のCTRが分かっているような理想的な状況を想定して、早期停止による期待損失への影響をシミュレーションしています。

  1. CTRの事前分布をそれぞれ Beta(10, 99900) とし、CTRをこの分布から生成する。
  2. 1で生成したCTRをパラメータとして、ABテストを模した20日間のデータを生成する。
  3. 2のデータを用いてCTRのパラメータの事後分布を推定する。
  4. 1 ~ 3の試行を40,000回繰り返す。
  5. 設定された閾値を下回る試行を抽出し、真の損失（L(\alpha, \beta): 1.で生成した値から算出される）を計算する。閾値と損失を記録する。
  6. 閾値を変更して5を繰り返す。

少し分かりにくいですが、ここで調べたいことは 手元のデータから得られる期待損失で意思決定をした時に、(本来は観測が出来ない)真の損失がどのような値を取るのか? ということになります。

以下にシミュレーションの結果を掲載します。
X軸が設定した閾値、Y軸が損失となります。peekingありの場合はなしの場合に比べて損失が高くなってしまいますが、閾値によらず、損失が設定した閾値(黒い点線)を超えることはありません。ここで、閾値は「誤った選択をした場合に許容できる損失の上限」を表すことを踏まえると、「期待損失を用いたベイズ法で意思決定を行えば、peekingの有無に依らず、設定した閾値以上の損失は起こらない」と解釈することが出来ます。 これが期待損失を用いたメリットと言えるでしょう。

ただし、繰り返しになってしまいますが、今回のシミュレーションのように適切に事前分布を設定出来た理想的な状況でも、peekingによって偽陽性は上がってしまうことには注意が必要です。

感想

  • この記事は、あくまで「期待損失に基づいて意思決定をする」ベイジアンABテストの話なので、他の指標を用いた場合どうなるのかが気になった。

    • ベイジアンファクター、ROPE、pdなど

  • 確かにベイズでもpeekingによって偽陽性は上がっているものの、閾値によってはpeekingの有無に依らず偽陽性を小さくすることは可能であるように感じた。検出力と併せて、以下の記事のようにシミュレーションを通じて適切な閾値を見つけるのが重要なのだと思った。

  • 効果がない施策に対して、「誤ってローンチしてしまう確率」を制御するのがNHST(p値)であり、「誤ってローンチした際の損失」を制御するのが期待損失を用いたベイズ法ということで、そもそも思想が異なるので、どちらを採用するのかは好みの問題なのかな?と感じた。

    • 偽陽性のコントロールは本質的でない！として今回のベイズ法を採用するのも悪くないが、記事でも触れられている通り、偽陽性が増大するということは無意味な施策をローンチし続けてしまう可能性がある。損失が発生することはないものの、開発の工数を差し引けば手放しに喜べるものではないだろう。
      • 期待損失に開発工数を組み込めば対応出来るかもしれない...?

  • 記事でも触れられているが、これをチームに普及していくのはハードルが高いように感じた。もちろんNHSTやp値のことをチーム全員が深く理解をするのも難しいが、とはいえ事前分布の設定やベイズ更新の実装、閾値の設定など、NHSTよりも難しいように感じた。

実装

Discussion