📊
Python における統計量・統計図のまとめ
この記事は Python Advent Calendar 2021 (カレンダー2)の23日目の記事です。
Python では幾つかのライブラリを用いてさまざまな統計量の計算や統計図の可視化を容易に行うことができる。本記事では、どのユースケースでどのライブラリを用いれば良いのかをまとめる。
※随時更新していく予定
記述統計量
位置
import numpy as np
import pandas as pd
from scipy import stats
import wquantiles
df = pd.DataFrame(np.random.randn(7, 2), index=pd.date_range("20211223", periods=7), columns=["value", "weight"])
# value weight
# 2021-12-23 1.476252 -0.340906
# 2021-12-24 0.642289 -0.409486
# 2021-12-25 0.640309 0.506255
# 2021-12-26 0.348381 -0.535211
# 2021-12-27 0.453124 0.136234
# 2021-12-28 0.088165 -0.633809
# 2021-12-29 0.115445 -0.096877
# 平均値 (mean)
df['value'].mean()
# 加重平均値 (weighted mean)
np.average(df['value'], weights=df['weight'])
# トリム平均値 (trimmed mean)
stats.trim_mean(df['value'], 0.2)
# 中央値 (median)
df['value'].median()
# 加重中央値 (weighted median)
wquantiles.median(df['value'], weights=df['weight'])
分散
import pandas as pd
import statsmodels.api as st
df = pd.DataFrame(np.random.randn(7, 2), index=pd.date_range("20211223", periods=7), columns=["value", "value_2"])
# value value_2
# 2021-12-23 -1.140660 -1.604924
# 2021-12-24 -0.135054 0.534193
# 2021-12-25 0.123041 0.527111
# 2021-12-26 -0.352537 -0.743234
# 2021-12-27 0.732284 -0.806847
# 2021-12-28 2.554425 -1.388672
# 2021-12-29 -1.214038 -0.978366
# 分散 (variance)
df['value'].var()
# 標準偏差 (standard deviation: SD)
df['value'].std()
# 平均絶対偏差 (mean absolute deviation)
df['value'].mad()
# 中央絶対偏差 (median absolute deviation: MAD)
st.robust.scale.mad(df['value'])
# パーセンタイル (percentile)
df['value'].quantile([0.05, 0.25, 0.5, 0.75, 0.95])
# 四分位範囲 (interquartile range: IRQ)
df['value'].quantile(0.75) - df['value'].quantile(0.25)
# 相関係数 (correlation coefficient)
df.corr()
# value value_2
# value 1.000000 -0.076202
# value_2 -0.076202 1.000000
統計図表
数値データ
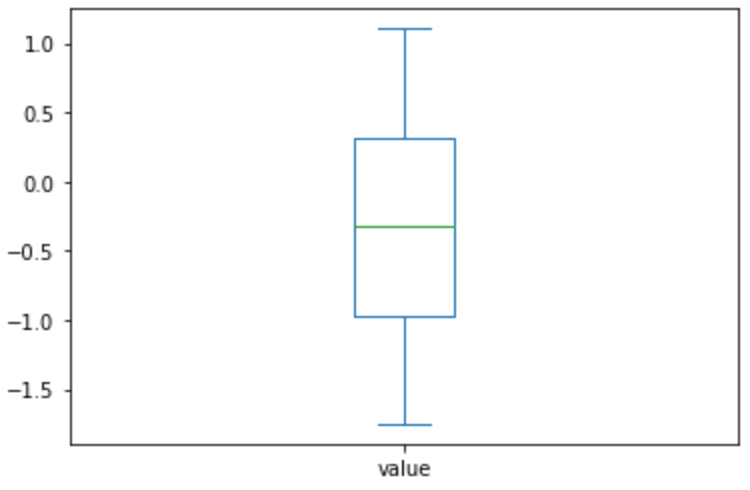
箱ひげ図
import numpy as np
import pandas as pd
df = pd.DataFrame(np.random.randn(7, 1), index=pd.date_range("20211223", periods=7), columns=["value"])
ax = df['value'].plot.box()
度数分布表
import numpy as np
import pandas as pd
df = pd.DataFrame(np.random.randn(7, 1), index=pd.date_range("20211223", periods=7), columns=["value"])
bins = pd.cut(df['value'], 10)
bins.value_counts()
# (-0.442, -0.269] 2
# (0.767, 0.94] 2
# (-0.789, -0.615] 1
# (-0.615, -0.442] 1
# (0.0762, 0.249] 1
# (-0.269, -0.0965] 0
# (-0.0965, 0.0762] 0
# (0.249, 0.422] 0
# (0.422, 0.594] 0
# (0.594, 0.767] 0
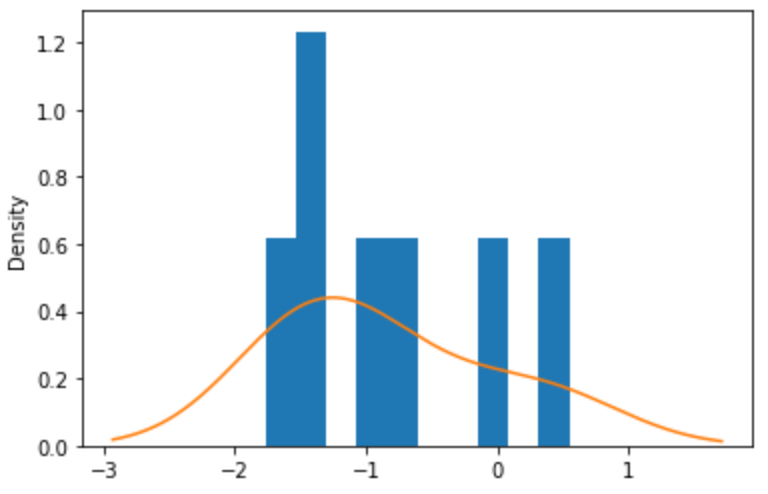
ヒストグラムと密度曲線
import numpy as np
import pandas as pd
df = pd.DataFrame(np.random.randn(7, 1), index=pd.date_range("20211223", periods=7), columns=["value"])
bins = pd.cut(df['value'], 10)
bins.value_counts()
カテゴリデータ
棒グラフ
import numpy as np
import pandas as pd
df = pd.DataFrame(np.random.randint(2, size=(7, 4)), index=pd.date_range("20211223", periods=7), columns=list("abcd"))
ax = df.sum().plot.bar()

標本分布
正規分布
from scipy import stats
import matplotlib.pyplot as plt
# 正規分布 N(0.2, 0.5^2) の確率密度関数の x = 0.1 の値
stats.norm.pdf(0.1, loc=0.2, scale=0.5)
# 正規分布 N(0.2, 0.5^2) の累積分布関数の x = 0.1 の値
stats.norm.cdf(0.1, loc=0.2, scale=0.5)
# 正規分布 N(0.2, 0.5^2) で乱数生成
stats.norm.rvs(loc=0.2, scale=0.5, size=100)
# QQ プロット
fig, ax = plt.subplots(figsize=(4, 4))
norm_sample = stats.norm.rvs(size=100)
stats.probplot(norm_sample, plot=ax)

二項分布
from scipy import stats
# 二項分布 B(5, 0.1) の確率質量関数の k = 2 の値
stats.binom.pmf(2, n=5, p=0.1)
# 二項分布 B(5, 0.1) の累積分布関数の k = 2 の値
stats.binom.cdf(2, n=5, p=0.1)
# 二項分布 B(5, 0.1) で乱数生成
stats.binom.rvs(n=5, p=0.1, size=100)
ポアソン分布
from scipy import stats
# ポアソン分布 Po(0.1) の確率質量関数の k = 2 の値
stats.poisson.pmf(2, mu=0.1)
# ポアソン分布 Po(0.1) の累積分布関数の k = 2 の値
stats.poisson.cdf(2, mu=0.1)
# ポアソン分布 Po(0.1) で乱数生成
stats.poisson.rvs(mu=0.1, size=100)
指数分布
from scipy import stats
# 指数分布 Ex(0.1) の確率密度関数の x = 2 の値
stats.expon.pdf(2, scale=10)
# 指数分布 Ex(0.1) の累積分布関数の x = 2 の値
stats.expon.cdf(2, scale=10)
# 指数分布 Ex(0.1) で乱数生成
stats.expon.rvs(scale=10, size=100)
Discussion