🔄

米田の補題を1枚の図式で描こう

2024/07/11に公開

圏論

概要

独学で米田の補題をやると，信じられないほど難しいと分かる．
何が信じられないかって，重要な補題らしいのに，簡単に説明出来ないことが信じられないので，もっと簡単に書けるやろという点に挑戦してみる．
米田の補題を1枚の図式にまとめてやろう．

今回はalg-d様の米田の補題のpdfを一枚の図式にしてみようと思う．

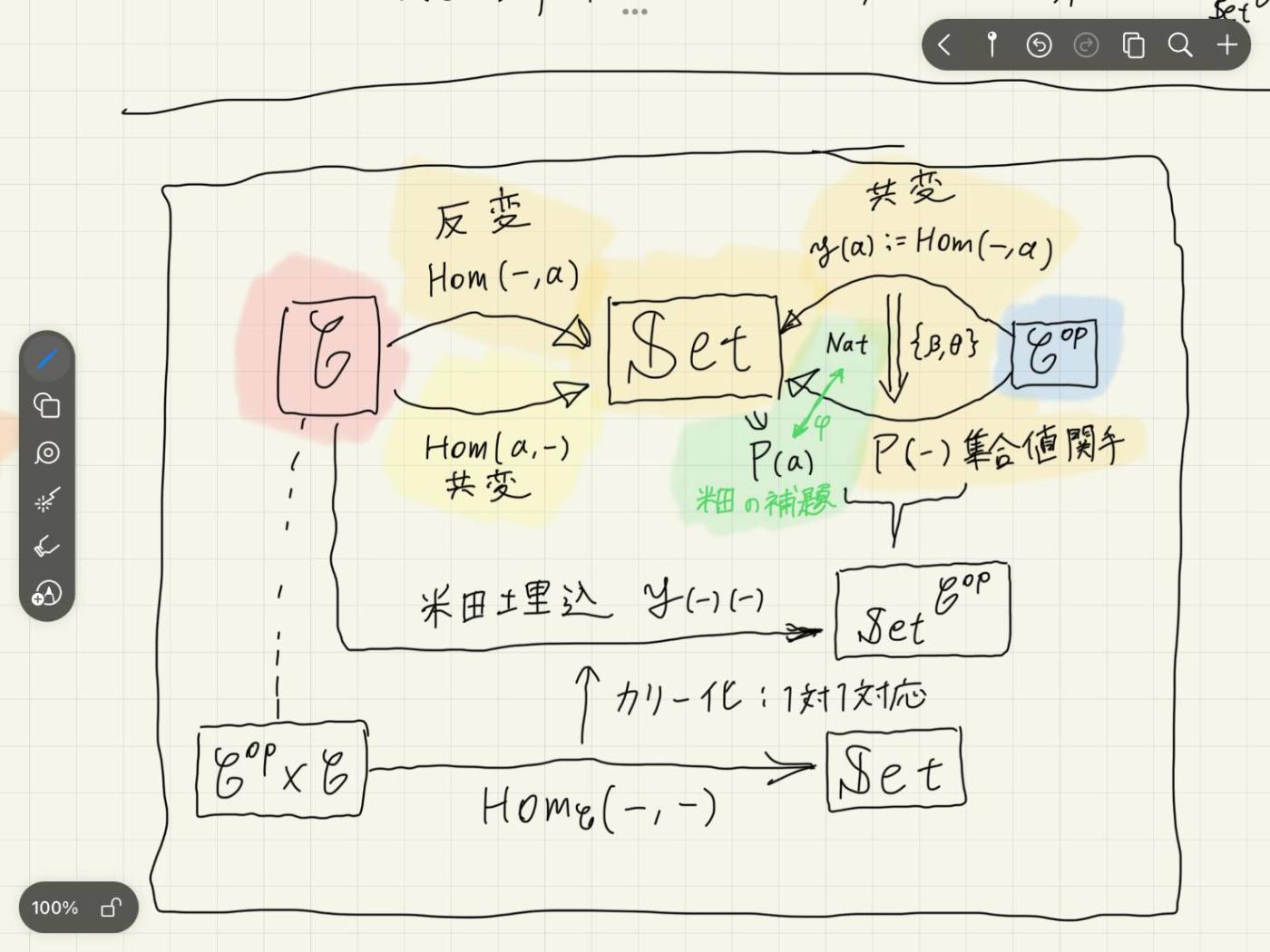
以下がその図式である．

結論：無理だった．調子にのってすみませんでした．

ファイルはこちらに置いておきます．（Kan拡張のメモとかも入っちゃってるけど）

もっと簡単に

この図式を見て落胆した方々，もう少し待っていただきたい．
この図式の大半はHom関手と逆射の定義を説明することに費やしてしまっている．
そこで，より簡単に書いてみよう．対象を全て取っ払うと以下のようになる．

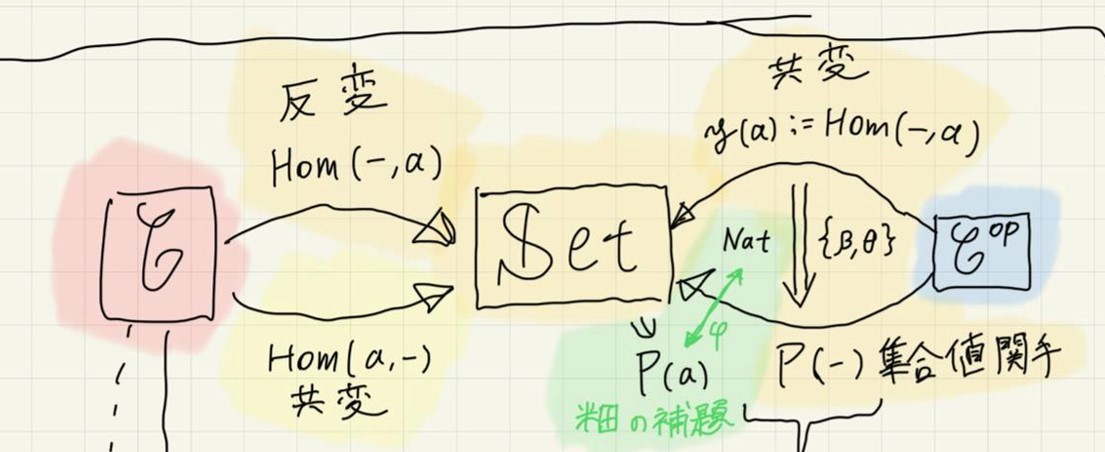
さらに言えば，米田の補題が言っていることは，図の緑の部分だけである．
そう思えば，まだギリ耐えられそうではないだろうか．いやそうでもないか．すみません．

証明の流れ

正直証明だけなら4まで飛ばしていいと思っています．こちとらアマチュアなので．

使う圏 $\mathscr{C}$ とHom関手を定義する
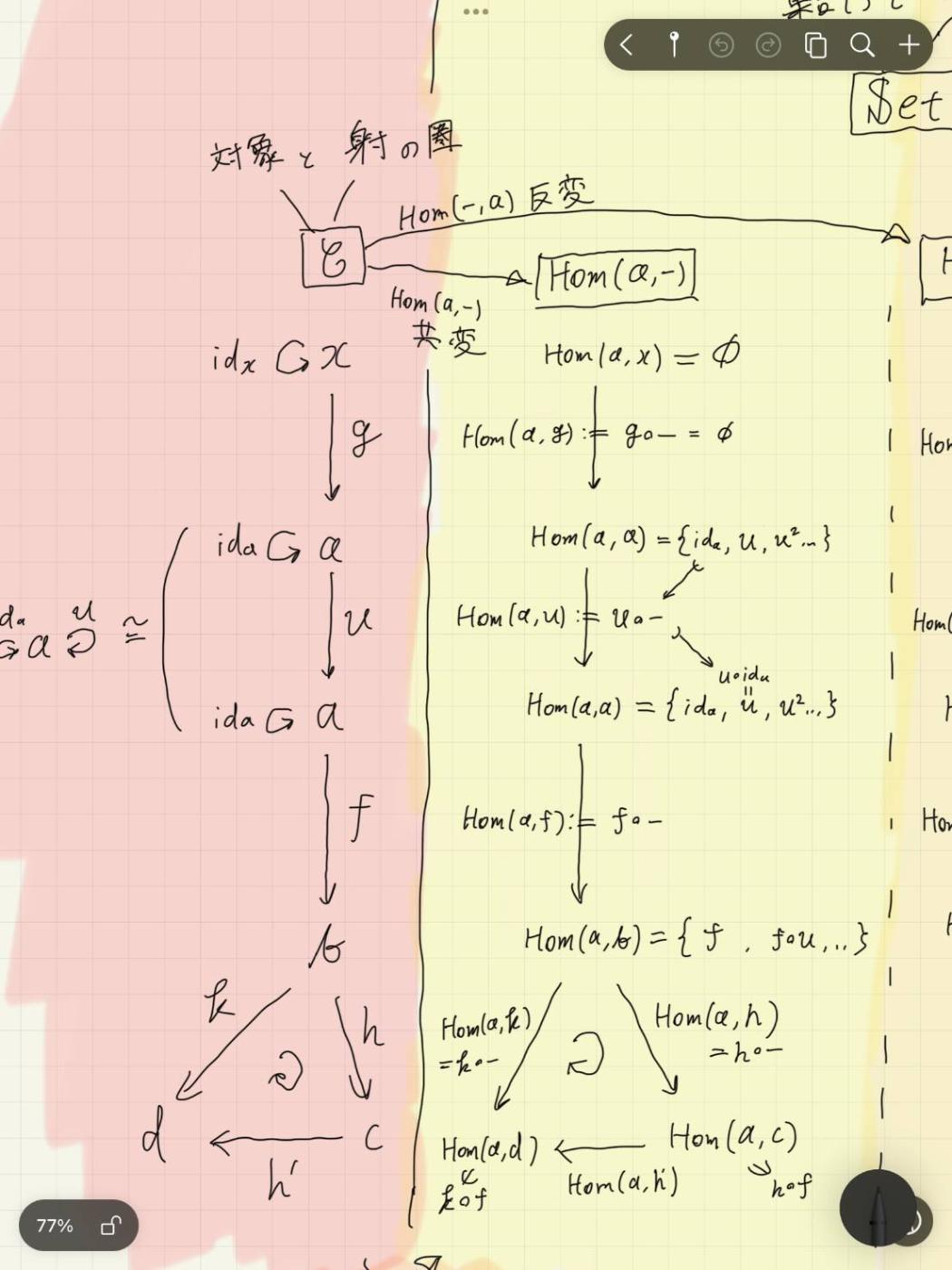
共変Hom関手はちゃんと関手になっているか？を確認する
反変関手 $y(a)$ , $P(a)$ （反対圏 $\mathscr{C}^{op}$ からの共変関手）に舞台を移す．（黄色・青部分）
米田の補題で使う自然変換を定義する（見つける）．
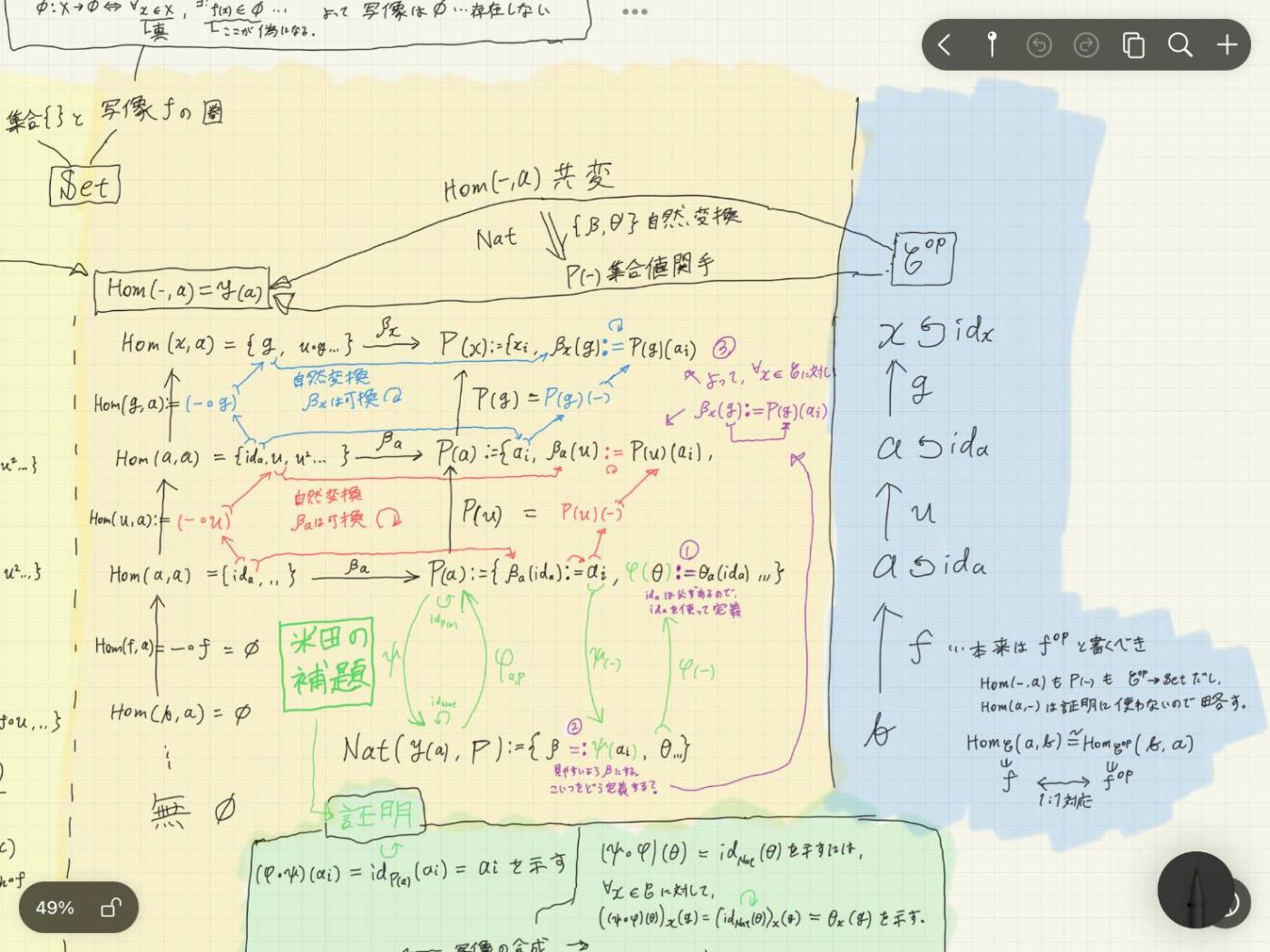
米田の補題を証明する．

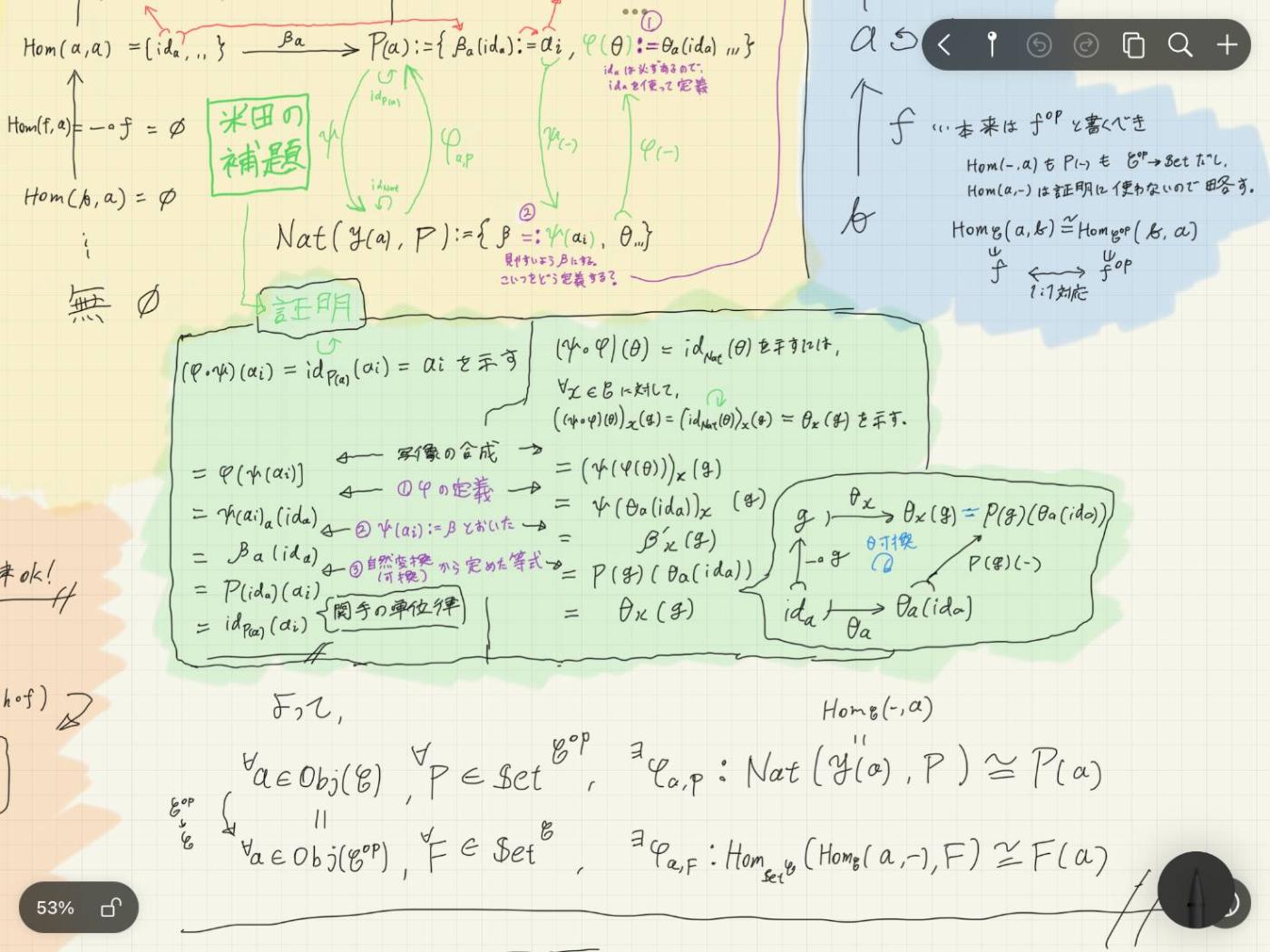
そうは言っても文章で読みたいという方は，元文献をご覧ください．

写像の細かい話

確認が取れてないので不安ですが，書いてみるとHom関手を考えるときに無から無への射とかがよく出てきました．以下を参照して，全て無 $\empty$ として考えています．

というのをメモしたのがこの辺

記法の話

それぞれの記号を使い分けて，識別しやすいwikipedia記法
$\forall{A}\in C, \forall{F}\in Set^{C} ; y:Nat(H^A,F)\cong F(A)$

Homだけで書けて，覚える記号が少ないalg-d記法
$\forall{a}\in C, \forall{P}\in Set^{C^{op}} ; \phi_{a,P}:Hom_{Set^{C^{op}}}(Hom(-,a),P(-))\cong Pa$

今回はいちいち書くのが面倒だったところを $Hom_{Set^{C^{op}}}=Nat$ と書くようにした．また， $f$ とか何回も出ていたので，その都度 $u$ とか $g$ とかに置き換えている．

昔の自分の疑問へ

Q. なんで $\mathscr{C}^{op}$ なんて使うの？普通の $\mathscr{C}$ でよくない？
A. 共変関手と反変関手を混ぜると，図のように射の向きがおかしくなるから．

Q. 結局この補題で何が出来るようになるの？実用の具体例を教えて
A. 圏論では対称ではなく射（つまり周りとの関係）を見れば特性（同型）が判別できることが証明できます
A. リバースエンジニアリングとかに使えます．
と思っていたけどリバースエンジニアリングの結果が当たり前すぎて萎えた．具体的には，「ある関数Fに，関数x^2を入力したら，[1,4,9,16]が返ってきた．これFに関数idを入れたら[1,2,3,4]が返ってくるから,
F内部のパラメータは[1,2,3,4]だ！」

そりゃそうでは？と思ってしまいました．すみません．内容はとても勉強になり感謝しています．

Q. 随伴・極限・モナド・Kan拡張・その他いろいろとのつながりは？
A. つながるけど証明は無くてもできます．すべての概念はKan拡張ですが，私のイメージだと「Kan拡張の側面もあってこんな見方もできます」くらいでいます．

このカリー化対応とか出てくると繋がってきます．

Q. 用語が多すぎる
A. 圏論は用語を作る学問っぽいので，自分の気になった圏だけメモするといいと思います．
圏論からは，「既存の表現で十分なのに，より一般化された言葉を開発していく」感じがします（誰かの文献にも書いてた）．
確かに圏とかどんどん新しいのが出てきて困る．

Q. NotionやZenn，Qiitaでノートまとめしたい
A. 諦めや．
逆に図式に慣れると，複雑な新言語を獲得したみたいな気分になってうれしくなれますヨ．

式の方が分かりやすいというのは気のせいなので，早く目を覚ましたほうがいいです．
https://www.youtube.com/watch?v=IAvrpd6s0D8&list=PLeBc8K3RvbSyoSx4NURPQPBsoPMJAr7Tm&index=15

Q. 表記が人によって異なるのっておかしくない？
A.

(https://www.youtube.com/watch?v=OVuYIMa5XBw)
でもそこでオリジナリティが出せます，気に入った人の記法を真似てリスペクトを示せます．そんな圏論が私は好きです．

終わりに

字が汚くてすみませんでした．
こんな記事でも目を通してくださり誠にありがとうございました．

今勉強している方へ，一人でも大丈夫です！私自身話せる人がいなくて1年を溶かしていますので！圏論勉強頑張ってください！

修正や素人質問，心を折るボディーブローのような質問もぜひお待ちしております．