ゼロから圏論をHaskellで実装するサンプルの一例

概要

圏論を勉強していると，人それぞれの記法があることが分かる．
恐ろしいことに，一人につき一つ，何なら1冊につき一つレベルである（半ギレ）．
さらに，Haskellでの実装しようにも，Haskell自体が型と関数の圏と呼ばれており，圏の中で圏を作るってどうなの？（全ギレ）

そこで，無茶苦茶抽象的な実装ではなく，もっと具体的な例を作ってみる．

Haskellを試すときはコンパイルではなく，ghciを起動し続けながらチェックすべし！

実行例

f x = x + 1 -- を書いたファイルtest.hsを作ったら
>ghci
-- で起動して，

-- 関数fを試したり
ghci> f 1
2

-- :tで関数fの型を確認したり，
ghci> :t f
f :: Num a => a -> a

-- :iで詳しい情報を見たり，
ghci> :i f
f :: Num a => a -> a    -- Defined at test.hs:1:1

-- 変更を加えたら:rでリロードしたりする．
ghci> :r 
Ok, one module loaded.

Haskellの読み方の基本

• haskellのすべては，型と式である．（変数も式扱い．ややこし）

なぜ型と式だけなのか？

それはラムダ計算がチューリング完全だからである
あらゆる計算・アルゴリズムを行うのが個別のチューリングマシンで，
それら個別のチューリングマシンを全て1基で再現できるのが万能チューリングマシンで，
ラムダ計算は万能チューリングマシンと等価であるチャーチ＝チューリングのテーゼがあって，
証明するには万能チューリングマシンを再現できることが証明された2タグシステムと同じだと証明されたウルフラムの2記号3状態チューリングマシンを再現できることを証明すればよい．マインクラフトやマリオメーカーなども，そうやって別の万能チューリングマシンを再現して証明してるらしい．
(wikiより，多少改変)

• 型は右結合A->B->C = A->(B->C)で大文字始まり
• 式は左結合f x y z = ((f x) y) zで小文字始まり
• 型を決めて，定義を決めるまでが，関数自作の1セット．

数式で書くと

$Int$を整数集合$\mathbb{Z}$としたとき
$x \in Int, f(x) \in Int$について

$$\begin{align*} f: & Int &\to & Int \\ & x &\mapsto & f(x) & := x + 1 \\ \end{align*}\\$$

と定義する．

$$f(2) = 2 + 1 = 3$$

である．
このように関数に2を入れて計算することを，Haskellでは関数適用という．fを2に適用して3になる．

コードで書くと

MyCategory

f :: Int -> Int -- 型の定義と
f x = x + 1     -- 式の定義

result = f 2 -- 関数適用

resultは3になる．

各部分の用語を書くと

Haskell用語

-- はコメントアウトです．

-- 関数 :: 型シグネチャ
関数 :: 型 -> 型
関数 値引数 = 式

となる．

ホントは $f:A\to B$， $a \mapsto f(a):=b$，のようにしたかったのだが，Haskellは型Cを対象として型シグネチャを書くのに対し，数学ではA,Bを集合として扱うため$f:C->C$としか書けなくなってしまう．

用語いろいろ（量がグロいので序盤は見ないほうがいいかも）

用語

-- data, classなどは構文なのでそのままにする

-- 対象：集合：型
data C = A | X | Y deriving (Show, Eq)
data 型名 = 値コンストラクタA | 値コンストラクタX | ...
data 圏C  = 対象A | 対象X | ... -- として扱う
-- deriving (Show, Eq)は，型Cを表示Showと比較Eqが出来る型にするという意味．ShowやEqは型クラス

-- 関手の定義
class Functor f where
    fmap :: (a -> b) -> (f a -> f b)
    -- 関手fなら射(a -> b)も射(f a -> f b)に写せるよな？の意味
class 型クラス 型 where
    型クラスにした型に付与する機能の定義

instance Functor F_cls where
    fmap f (F x) = F (f x) -- F(f)(F(x))
instance 型クラス 型クラスを付与する型 where
    fmap 射の写し方のルール設定

以上，用語をまとめると，以下のようになる．ここで一度，用語の多さにキレておくとよい．

用語	実装例	一言
型	C, F_cls C	圏として扱う．必ず大文字
値コンストラクタ	A, X, F A, G X	対象として扱う．必ず大文字
式・関数	f, g, h	射として扱う
型シグネチャ	C, F_cls C	射のどっからどこへの詳細情報
引数	a, b, x, y	必ず小文字
型クラス	Show, Eq, Functor, Applicative	型に機能を追加する
型コンストラクタ	F_cls a, G_cls a	型引数aを取っている"型"
インスタンス	F_cls, G_cls	型に型クラスの機能を付与したもの

他にも，具体型：F_cls Intのように型コンストラクタに型を具体的に入れたやつとか，
ファンクター値，アプリカティブ値：それぞれのインスタンスの具体的な値F Yとか，
めちゃくちゃあるが，今は無視していい．

圏

• 圏論の全ては射で説明できるらしいが，そうは言われても分らんので，圏論＝対象と射の学問ととらえる．
• 圏は，射の合成条件：結合律と恒等射により，うまい具合に関係性を保って議論できる．（コヒーレンス則？）

記法(tex)と定義wiki

圏$\mathscr{C}$は

• 対象の類 $A,X,Y \in Obj(\mathscr{C}) = \{A,X,Y\}$
• 射の類 $f,g,h,h' \in Mor(\mathscr{C}) = \{f,g,h,h',id_A, id_X, id_Y, id_Z\}$(結合したもの（生成した射と呼ぶ）を含めるともっとあるが，多いので省く)
• 結合律を満たす射の合成 $h \circ f$
• 単位律を満たす恒等射 $id_A, id_X, id_Y$
  からなる．
• 結合律は順番どれでもOK条件で，$h' \circ h \circ f = (h' \circ h) \circ f = h' \circ (h \circ f)$
• 単位律はどっちから来ても射はそのままです条件で，$id_A \circ f = f = f \circ id_X, id_X \circ h = h$

以上が圏の定義である．

また，可換とは，ルートの異なる（始域と終域が同じだが射が異なる）射の交換が可能なことを指す．$h \circ f = g$であるため今回は可換である．

（類は集合のあやふやバージョン．集合の集合（族）とかも含んでいる）

手書き

真ん中のぐるぐるが可換を表す．ぐるぐるするというより置き換え可能というイメージのほうが良い．

Haskell

ken

-- 対象：集合：型
data C = A | X | Y | Z deriving (Show, Eq)

-- 射：関数
f :: C -> C
f A = X
g :: C -> C
g A = Y
h :: C -> C
h X = Y
h' :: C -> C
h' Y = Z

-- 恒等射
idA :: C -> C
idA a = a
idX :: C -> C
idX x = x
idY :: C -> C
idY y = y
idZ :: C -> C
idZ z = z
-- 以下，恒等射にはデフォルトで搭載されているidを用いる．


-- 射の合成
--- 以下，===で同じという意味を表すことにする
-- テスト(h.f) A === 結果Y

-- 結合律
-- (h'.h.f) A === ((h'.h).f) A === (h'.(h.f)) A === Z

-- 可換かどうか
result1 = (h.f) A
result2 = g A
kakan = (result1 == result2) -- Trueなので可換 h.f=g

関手

ここからHaskellの難所．

記法ルール(tex)と定義

関手$F$とは，対象と射を同時に写す射である．
関手$F$のシグネチャは

$$F:\mathscr{C}\to \mathscr{D}$$

と書き，以下の条件を満たす．

• $X,Y\in Obj{\mathscr{C}}$に対して，$F(X),F(Y)\in Obj{\mathscr{D}}$ を対応させる．
• $f:X\to Y$に対して，$F(f):F(X)\to F(Y)$を対応させる
• 結合律は，$h\circ f$に対して，$F(h\circ f) = F(h)\circ F(f)$
• 単位律は，$id_A$に対して，$F(id_A)=id_{F(A)}$

手書き

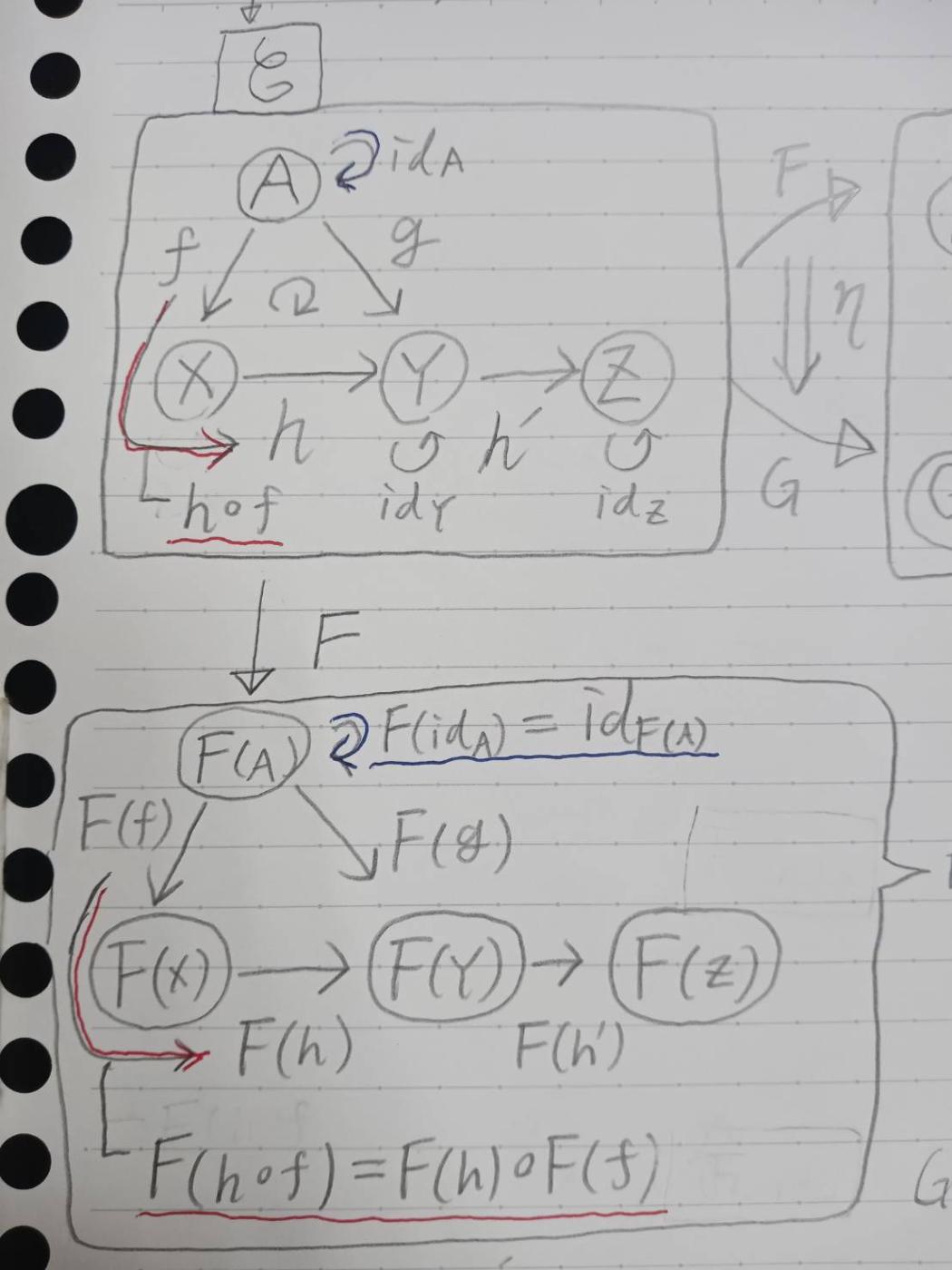
Haskell

kansyu

-- FunctorとApplicativeは中身の確認のため自作するので隠しておく
import Prelude hiding (Functor(..), Applicative(..))

{-
この辺に圏で書いたコード
-}


-- 関手の定義 --
class Functor f where
    fmap :: (a -> b) -> (f a -> f b)
    -- 関手fなら射(a -> b)も射(f a -> f b)に写せるよな？
class (Functor f) => Applicative f where
    -- aを受け取って，アプリカティブ値(f a)を返す．つまり対象写す
    pure :: a -> f a
    -- fmap強化版つまり射写す
    (<*>) :: f (a -> b) -> (f a -> f b)

-- 対象（型）を作る
data F_cls a = F a deriving (Show)
-- 中身を関手化
instance Functor F_cls where
    fmap f (F x) = F (f x) -- F(f)(F(x))
instance Applicative F_cls where
    pure x = F x
    F f <*> F x = fmap f (F(x)) -- = F (f x) = F(f)(F(x))




-- 関手の条件 --
-- 射を正しく写しているか？：F(f) <*> F(A) === F(X)

(<.>) :: F_cls (b -> c) -> F_cls (a -> b) -> F_cls (a -> c)
F h <.> F f = F(h.f)
-- 結合律：F(h.f) <*> F(A) === F(h) <.> F(f) <*> F(A) === (F Y)

idFA :: F_cls C -> F_cls C
idFA a = a
-- 恒等射：F(idA) <*> F(A) === idFA(F(A)) === F(A)

自然変換

こいつが厄介．
「自然な～」という初心者からすると超不自然な単語の元凶
私は圏論から学び始めたので，関手の上位互換だと勝手に誤解していたが，射は写さない．繰り返す．関手と異なり射は写さない

記法ルール(tex)と定義

自然変換$\eta$は射の類$\{\eta_A,\eta_X,\eta_Y,\eta_Z\}$で，以下のような可換な射の束である，圏$\mathscr{D}$内の射である．

$$G(h)\circ \eta_X = \eta_Y \circ F(h)$$

左下ルート＝右上ルートで可換である．
また，複数の射の束であり，２次元的に広がることから，以下のようにも書かれる

$$\eta:F\Rightarrow G$$

手書き

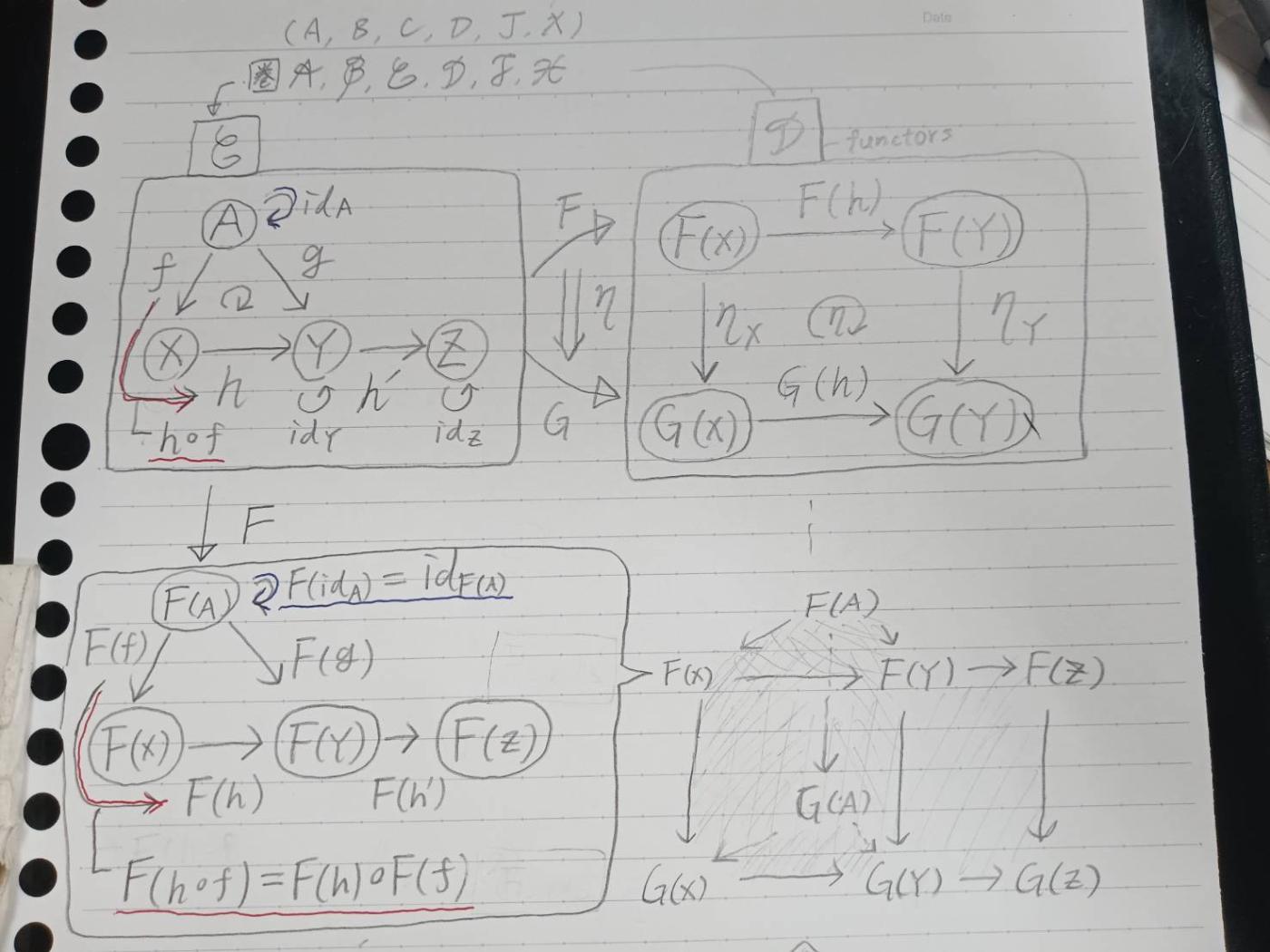
全て書き出すと立方体のようになる．
対象が点で射が辺，自然変換が下に延び3次元になる．

Haskell

sizen_henkan

-- ここから上は圏と関手のコード

-- 関手をもう一個用意:G
data G_cls a = G a deriving (Show)
instance Functor G_cls where
    fmap f (G x) = G (f x) -- F(f)(F(x))

instance Applicative G_cls where
    pure x = G x
    G f <*> G x = fmap f (G x) -- = F (f x) = F(f)(F(x))

-- 自然変換nを定義
n_A :: F_cls C -> G_cls C
n_A(F(A)) = G A
n_X :: F_cls C -> G_cls C
n_X(F(X)) = G X
n_Y :: F_cls C -> G_cls C
n_Y(F(Y)) = G Y
n_Z :: F_cls C -> G_cls C
n_Z(F(Z)) = G Z
n = [n_A, n_X, n_Y, n_Z] -- 自然変換は上記のセット

-- 可換条件
-- G(h) <*> (n_X(F X)) === n_Y(F(h)<*>F(X)) === G Y

自然変換を適用するやり方が，数式に寄せれず少し悔しく思っている．

米田の補題

調整中．分らなすぎる．
リバースエンジニアリングできるっぽい

よ談

https://m-hiyama.hatenablog.com/entry/2023/06/06/152024
米田埋め込みを表す数学記号として，日本語平仮名の"よ"が使われてたことがあったらしい．
余米田の補題が存在$\exist$したり，米田写像$よ$が存在する$\exist$．
なんだかとってもうれしいね．

全コードまとめ

MyCategory

-- 20240516_0:42_完全に理解した

-- 20240624_圏論なんもわからん

-- 型と関数の圏Hask

-- FunctorとApplicativeは中身の確認のため自作するので隠しておく
import Prelude hiding (Functor(..), Applicative(..))

-- 対象：集合：型
data C = A | X | Y | Z deriving (Show, Eq)

-- 射：関数
f :: C -> C
f A = X
g :: C -> C
g A = Y
h :: C -> C
h X = Y
h' :: C -> C
h' Y = Z

-- 恒等射
idA :: C -> C
idA a = a
idX :: C -> C
idX x = x
idY :: C -> C
idY y = y
idZ :: C -> C
idZ z = z
-- 以下，恒等射にはデフォルトで搭載されているidを用いる．


-- 射の合成
--- 以下，===で同じという意味を表すことにする
-- テスト(h.f) A === 結果Y

-- 結合律
-- (h'.h.f) A === ((h'.h).f) A === (h'.(h.f)) A === Z

-- 可換かどうか
result1 = (h.f) A
result2 = g A
kakan = (result1 == result2) -- Trueなので可換 h.f=g




-- 関手の定義 --
class Functor f where
    fmap :: (a -> b) -> (f a -> f b)
    -- 関手fなら射(a -> b)も射(f a -> f b)に写せるよな？
class (Functor f) => Applicative f where
    -- aを受け取って，アプリカティブ値(f a)を返す．つまり対象写す
    pure :: a -> f a
    -- fmap強化版つまり射写す
    (<*>) :: f (a -> b) -> (f a -> f b)

-- 対象（型）を作る
data F_cls a = F a deriving (Show)
-- 中身を関手化
instance Functor F_cls where
    fmap f (F x) = F (f x) -- F(f)(F(x))
instance Applicative F_cls where
    pure x = F x
    F f <*> F x = fmap f (F(x)) -- = F (f x) = F(f)(F(x))




-- 関手の条件 --
-- 射を正しく写しているか？：F(f) <*> F(A) === F(X)

(<.>) :: F_cls (b -> c) -> F_cls (a -> b) -> F_cls (a -> c)
F h <.> F f = F(h.f)
-- 結合律：F(h.f) <*> F(A) === F(h) <.> F(f) <*> F(A) === (F Y)

idFA :: F_cls C -> F_cls C
idFA a = a
-- 恒等射：F(idA) <*> F(A) === idFA(F(A)) === F(A)



-- 関手をもう一個用意:G
data G_cls a = G a deriving (Show)
instance Functor G_cls where
    fmap f (G x) = G (f x) -- F(f)(F(x))

instance Applicative G_cls where
    pure x = G x
    G f <*> G x = fmap f (G x) -- = F (f x) = F(f)(F(x))

-- 自然変換n
n_A :: F_cls C -> G_cls C
n_A(F(A)) = G A
n_X :: F_cls C -> G_cls C
n_X(F(X)) = G X
n_Y :: F_cls C -> G_cls C
n_Y(F(Y)) = G Y
n_Z :: F_cls C -> G_cls C
n_Z(F(Z)) = G Z
n = [n_A, n_X, n_Y, n_Z] -- 自然変換は上記のセット

-- 可換条件確認
-- G(h) <*> (n_X(F X)) === n_Y(F(h)<*>F(X)) === G Y