材料力学の梁問題のシミュレータを作った（完全版）

はじめに

前回、sympyを用いて固定端の片持ち梁を解析しました。
（https://zenn.dev/halmet7000/articles/000fe097378382）

今回はそれを一般化できたので共有します。
時間がなかったため記事内容はカスです。すみません。
過去問の答え合わせやsympyの練習にどうぞ。
colab:https://colab.research.google.com/drive/1LiBu57fFNymdoTkepuPB8pNtS_BBISqx?usp=sharing

入力と出力の例

![]
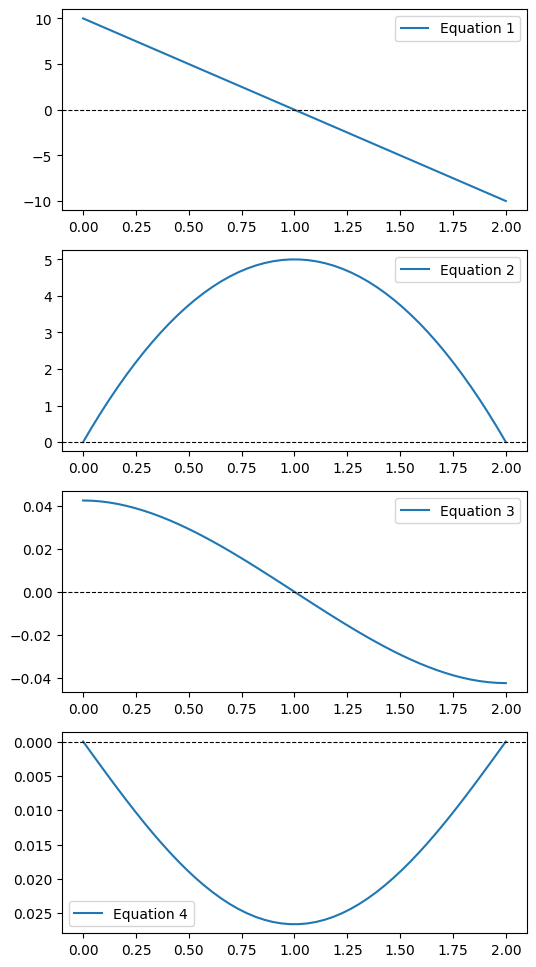
これのSFD,BMD,たわみ角,たわみのグラフが正しく出力されるか見てみます。上から順に1,2,3,4,5,6とします。

1.両端支持梁-点荷重

・両端支持梁は▲で、点荷重は↓で出ます。

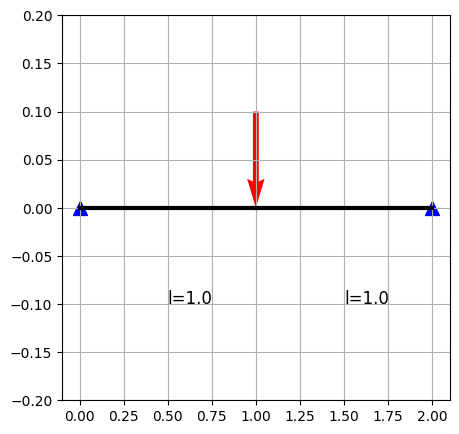
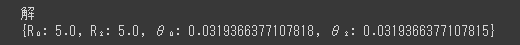
2.両端支持梁-等分布荷重

・等分布荷重は横帯で出ます

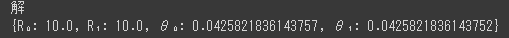
3.両端支持梁-モーメント

・モーメントは赤丸○で出ます。

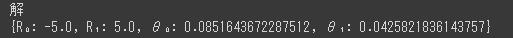
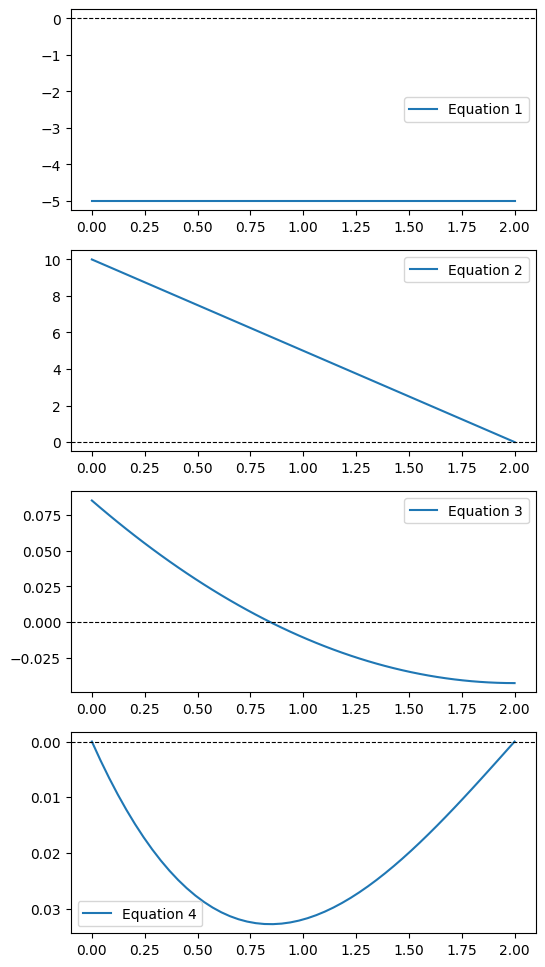
4.片持ち梁-点荷重

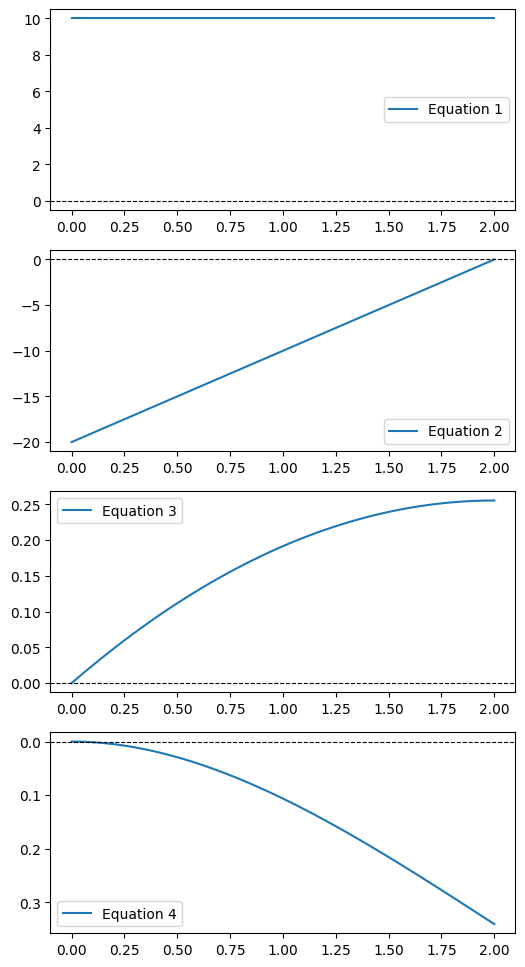
5.片持ち梁-等分布荷重

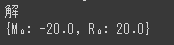
6.片持ち梁-モーメント

プログラムの概要

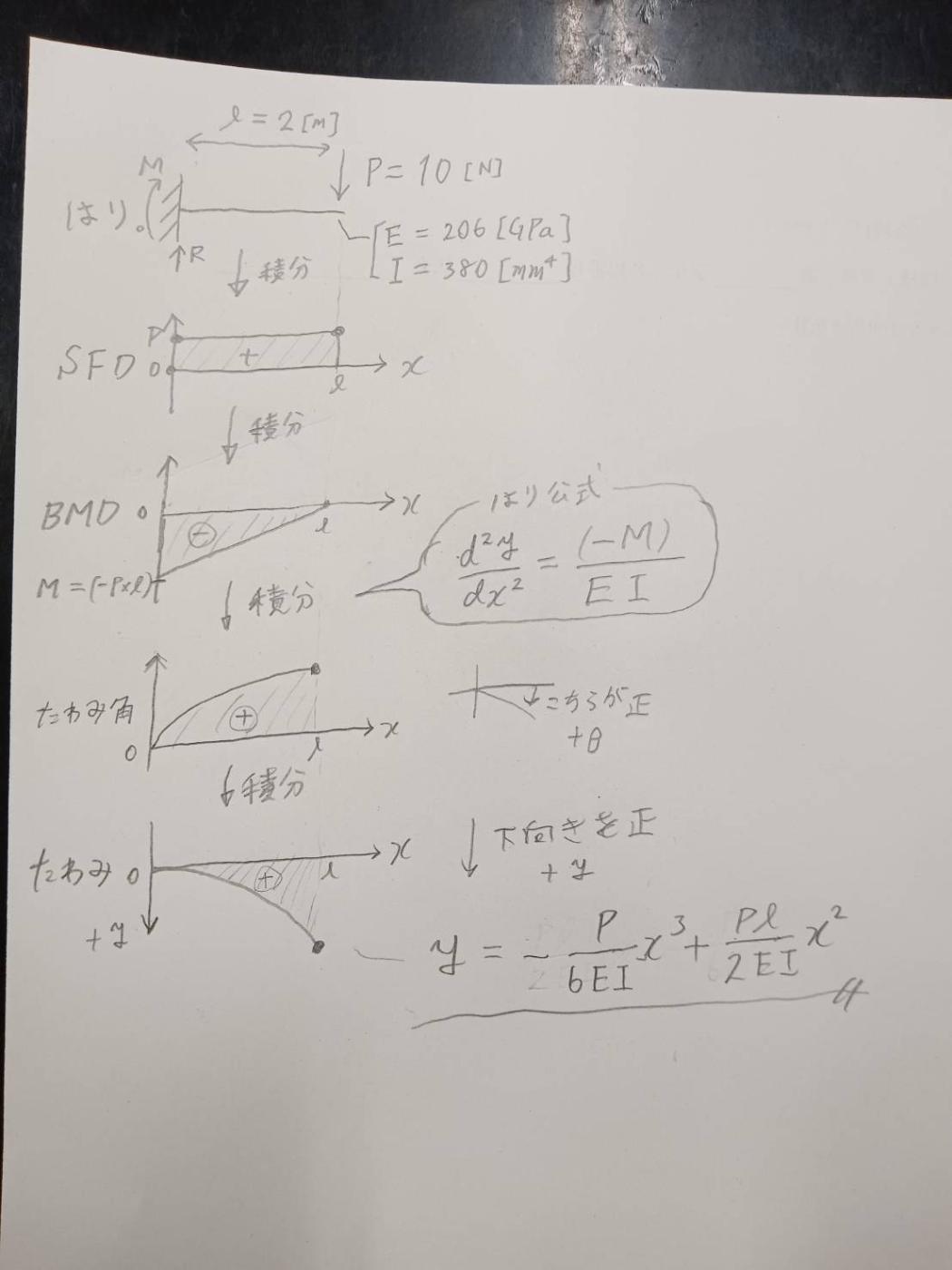
上記図のように、初歩的な梁問題は大体積分していくだけの問題です。
なので、まず
・支持部分（プログラム上ではノード）がどうなっているか決めて
・その右側に梁（プログラム上ではエッジ）を伸ばし
・荷重がどうなってるか指定する
を繰り返して梁データを作っていきます。
次に
・sympyでデータから式を解く
・ノード部分で式が変わるので、境界条件をそろえて次の式を解く
を繰り返し、最後に梁の右端の境界条件を使った連立方程式を解いて未知数を求めます。
あとは表示したり小手先のことをして終了です。

後ろのほうに入力を省いた両端支持梁だけの仮プログラムを乗せたので理解の助けになれば幸いです。

プログラム本体

beam_simu.py

from sympy import sympify, pprint, diff, Function, solve, dsolve, Eq, Derivative, symbols, lambdify
import matplotlib.pyplot as plt
import numpy as np
import japanize_matplotlib

values = {
    "E":206*10**9,
    "I":380*10**-12,
}
print("以下の断面係数が正しいか確認してください：")
print(values)


print("プログラムを開始します。")
# 入力用関数
def add_node_data(node_data_list, node_type, x, P=0., M=0.):
    index = len(node_data_list)
    if node_type == "Fixed":
        node_data_list.append(
            {
                "x":x,
                "F":symbols(f"R{index}"),
                "M":symbols(f"M{index}"),
                "θ":0,
                "δ":0,
            }
        )
    elif node_type == "Supported":
        node_data_list.append(
            {
                "x":x,
                "F":symbols(f"R{index}"),
                "M":M,
                "θ":symbols(f"θ{index}"),
                "δ":0,
            }
        )
    elif node_type == "Free":
        node_data_list.append(
            {
                "x":x,
                "F":P,
                "M":M,
                "θ":0,
                "δ":0,
            }
        )
    return node_data_list

def add_edge_data(edge_data_list, l, q):
    if not l == 0:
        edge_data_list.append(
            {
                "l":l,
                "q":q,
            }
        )
    return edge_data_list


""" 描画・入力フェーズ """
# 軸範囲の設定
lim = 0.2
plt.ylim(-lim, lim)
y_size = lim/2 # ベクトルなどのサイズ
# グリッド表示
plt.grid()
# ラベル表示
plt.legend()

# ノードを描画
def draw_node(x:float, mode:str, P:float, M:float):
    if mode == "Supported":
        # 支持端を描画
        plt.scatter(x, 0, marker='^', color='blue', s=100, label="支持端")
    if mode == "Fixed":
        # 固定端を描画
        plt.scatter(x, 0, marker='s', color='blue', s=700, label="固定端")

    # 文字式でないのなら、荷重
    if not P == 0:
        # 荷重を描画
        plt.quiver(x, y_size, 0, -y_size, angles='xy', scale_units='xy', scale=1, color='red', width=0.015, label="荷重")
    if not M == 0:
        # モーメントを描画
        plt.scatter(0.5, 0, linewidths=3, color="white",ec='red', s=100, label="モーメント")

# 梁を描画
def draw_edge(x:float, l:float, q:float):
    # 梁を描画
    plt.plot([x, x+l], [0,0], color='black', linewidth=3)
    # 梁の長さテキストを追加
    plt.text(x+l/2, -y_size, f"l={l}", fontsize=12, color='black')
    # 分布荷重を描画
    if not q == 0:
        rectangle = plt.Rectangle((x, 0), l, y_size, color='red', alpha=0.5)
        plt.gca().add_patch(rectangle)

# 描画・入力
node_type_list = ["Free", "Fixed", "Supported"]
now_x = 0
node_data_list = []
edge_data_list = []
while True:
    print("ノード入力")
    node_type = node_type_list[int(input("node(Free:0, Fixed:1, Supported:2)>>>"))]
    add_P = float(input("add force (  ↑+  ): P="))
    add_M = float(input("add moment(clock+): M="))
    # 描画
    draw_node(
        x=now_x,
        mode=node_type,
        P=add_P,
        M=add_M,
    )
    # リスト格納
    node_data_list = add_node_data(
        node_data_list=node_data_list,
        node_type=node_type,
        x=now_x,
        P=add_P,
        M=add_M,
    )

    print("エッジ入力")
    l = float(input("ノード間長さ(l=0で終了)：l="))
    if l == 0:
        print("入力完了")
        break
    q = float(input("等分布荷重：q="))
    # 描画
    draw_edge(
        x=now_x,
        l=l,
        q=q,
    )
    # リスト格納
    edge_data_list = add_edge_data(
        edge_data_list=edge_data_list,
        l=l,
        q=q,
    )
    # x更新
    now_x += l
    
    # グラフを表示
    plt.pause(0.1)

print(node_data_list)
print(edge_data_list)
print("梁グラフを表示")
plt.pause(0.1)


""" 解析フェーズ """
print("解析開始")
# 積分していって公式を生成する関数
def generate_formulae(q, bc_x, bc_F, bc_M, bc_theta, bc_delta):
    x = symbols('x')
    E, I = symbols('E I')
    F = Function('F')(x)
    M = Function('M')(x)
    theta = Function('θ')(x)
    delta = Function('δ')(x)

    # SFDを求める微分方程式 dF(x)/dx = q = 等分布荷重
    SFD = dsolve(
        Eq(Derivative(F, x), q),
        func=F,
    )
    # 境界条件から積分定数を計算、代入 bc_F = F(bc_x)
    F0 = solve(bc_F - SFD.subs("x", bc_x).rhs)[0]
    if not type(F0) == dict:
        M0 = {"C1":F0}
    SFD = SFD.subs(F0)


    # BMDを求める微分方程式 dM(x)/dx = F(x)
    BMD = dsolve(
        Eq(Derivative(M, x), SFD.rhs),
        func=M,
    )
    # 境界条件から積分定数を計算、代入 bc_M = M(bc_x)
    M0 = solve(bc_M - BMD.subs("x", bc_x).rhs)[0]
    if not type(M0) == dict:
        M0 = {"C1":M0}
    BMD = BMD.subs(M0)


    # たわみ角を求める d^2y/dx^2 = dθ/dx = -M(x)/EI
    defl_angle = dsolve(
        Eq(Derivative(theta, x), -BMD.rhs/(E*I)),
        func=theta,
    )
    # 境界条件から積分定数を計算、代入 bc_θ = θ(bc_x)
    theta0 = solve(bc_theta - defl_angle.subs("x", bc_x).rhs)[0]
    if not type(theta0) == dict:
        theta0 = {"C1":theta0}
    defl_angle = defl_angle.subs(theta0)


    # たわみを求める dy/dx= θ(x)
    deflection = dsolve(
        Eq(Derivative(delta, x), defl_angle.rhs),
        func=delta,
    )
    # 境界条件から積分定数を計算、代入 bc_δ = δ(bc_x)
    delta0 = solve(bc_delta - deflection.subs("x", bc_x).rhs)[0]
    if not type(delta0) == dict:
        delta0 = {"C1":delta0}
    deflection = deflection.subs(delta0)

    return SFD, BMD, defl_angle, deflection





# 最初の式
SFD, BMD, defl_angle, deflection = generate_formulae(
    q=edge_data_list[0]["q"],
    bc_x=node_data_list[0]["x"],
    bc_F=node_data_list[0]["F"],
    bc_M=node_data_list[0]["M"],
    bc_theta=node_data_list[0]["θ"],
    bc_delta=node_data_list[0]["δ"],
)
print(f"formulae_{0}{1}")
pprint(SFD)
pprint(BMD)
pprint(defl_angle)
pprint(deflection)

SFD_list = [SFD]
BMD_list = [BMD]
defl_angle_list = [defl_angle]
deflection_list = [deflection]

for i in range(1, len(edge_data_list)):
    bc_x = node_data_list[i]["x"]
    SFD, BMD, defl_angle, deflection = generate_formulae(
        q=edge_data_list[i]["q"],
        bc_x=bc_x,
        bc_F=SFD_list[i-1].subs("x", bc_x).rhs + node_data_list[i]["F"],
        bc_M=BMD_list[i-1].subs("x", bc_x).rhs + node_data_list[i]["M"],
        bc_theta=defl_angle_list[i-1].subs("x", bc_x).rhs + node_data_list[i]["θ"],
        bc_delta=deflection_list[i-1].subs("x", bc_x).rhs + node_data_list[i]["δ"],
    )
    print(f"formulae_{i}{i+1}")
    pprint(SFD)
    pprint(BMD)
    pprint(defl_angle)
    pprint(deflection)
    # データ追加
    SFD_list.append(SFD)
    BMD_list.append(BMD)
    defl_angle_list.append(defl_angle)
    deflection_list.append(deflection)


print("最後の点")
bc_x = node_data_list[-1]["x"]
# 力のつり合いとモーメントのつりあいの連立方程式
sigmaF = SFD_list[-1].subs("x", bc_x).rhs + node_data_list[-1]["F"]
sigmaM = BMD_list[-1].subs("x", bc_x).rhs + node_data_list[-1]["M"]
sigmatheta = defl_angle_list[-1].subs("x", bc_x).rhs + node_data_list[-1]["θ"]
sigmadelta = deflection_list[-1].subs("x", bc_x).rhs + node_data_list[-1]["δ"]
# 具体値を入れて計算
simultaneous_equations = [
    sigmaF.subs(values),
    sigmaM.subs(values),
    sigmatheta.subs(values),
    sigmadelta.subs(values),
]
# 解く
reaction_force = solve(simultaneous_equations)
print("解")
pprint(reaction_force)




"""描画フェーズ"""
solutions = [
    [expr.subs(values).subs(reaction_force) for expr in SFD_list],
    [expr.subs(values).subs(reaction_force) for expr in BMD_list],
    [expr.subs(values).subs(reaction_force) for expr in defl_angle_list],
    [expr.subs(values).subs(reaction_force) for expr in deflection_list],
]

# グラフの描画
fig, axs = plt.subplots(4, 1, figsize=(6, 12))

# プロット用x軸
iter_num = len(edge_data_list)
x_values = [np.linspace(float(node_data_list[i]["x"]), float(node_data_list[i+1]["x"]), 50) for i in range(iter_num)]
# 各式をプロット
for i, solution in enumerate(solutions): # 4式分繰り返し
    # 梁の分断数分の処理
    for j in range(iter_num):
        # 解をNumPy関数に変換
        expr = solution[j].rhs
        expr_numpy = lambdify(symbols("x"), expr, "numpy")

        # 描画
        if type(expr_numpy(x_values[j])) == float: # 定数式のとき
            axs[i].plot(x_values[j], expr*np.ones_like(x_values[j]), label=f'Equation {i+1}')
        else:
            axs[i].plot(x_values[j], expr_numpy(x_values[j]), label=f'Equation {i+1}')
        axs[i].axhline(0, color='black', linewidth=0.8, linestyle='--')
        axs[i].legend()
# 梁たわみ反転
axs[3].invert_yaxis()

# グラフの表示
plt.show()

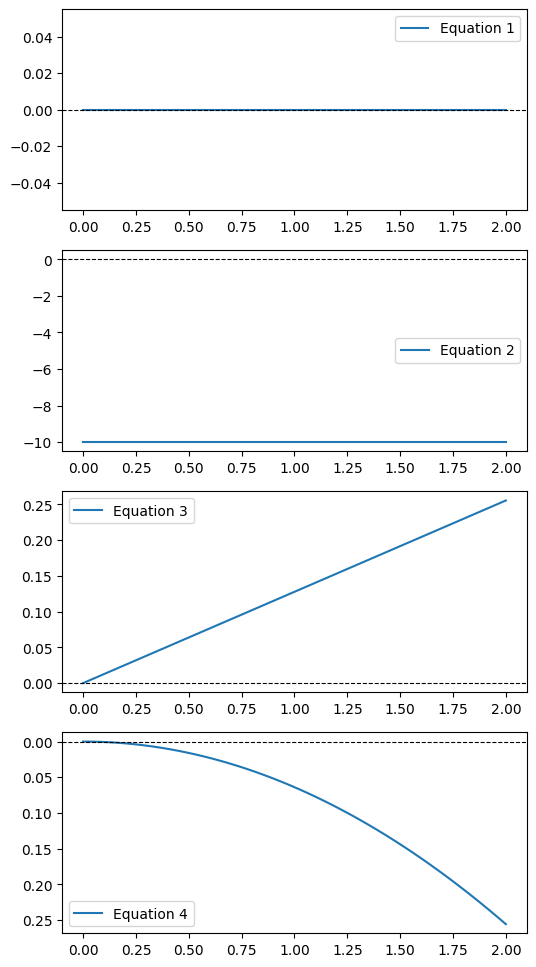
理解の補助：両端支持梁のみの試作

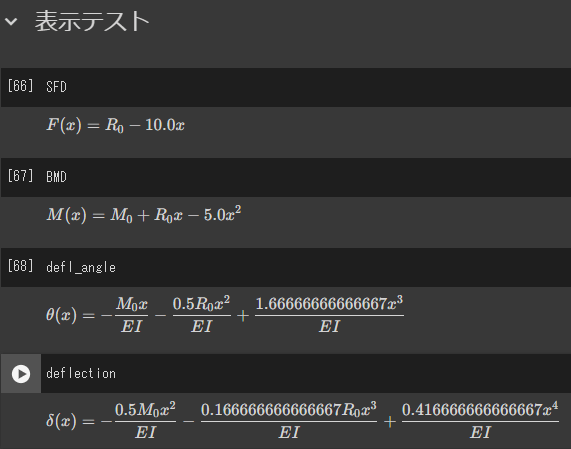
出力

スクリプト

ryo_ta_shiji_hari.py

from sympy import pprint, Function, dsolve, solve, Eq, Derivative, symbols, lambdify
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np


# 積分していって公式を生成する関数
def generate_formulae(q, bc_x, bc_F, bc_M, bc_theta, bc_delta):
    x = symbols('x')
    E, I = symbols('E I')
    F = Function('F')(x)
    M = Function('M')(x)
    theta = Function('θ')(x)
    delta = Function('δ')(x)

    # SFDを求める微分方程式 dF(x)/dx = q = 等分布荷重
    SFD = dsolve(
        Eq(Derivative(F, x), q),
        func=F,
    )
    # 境界条件から積分定数を計算、代入 bc_F = F(bc_x)
    F0 = solve(bc_F - SFD.subs("x", bc_x).rhs)[0]
    if not type(F0) == dict:
        M0 = {"C1":F0}
    SFD = SFD.subs(F0)


    # BMDを求める微分方程式 dM(x)/dx = F(x)
    BMD = dsolve(
        Eq(Derivative(M, x), SFD.rhs),
        func=M,
    )
    # 境界条件から積分定数を計算、代入 bc_M = M(bc_x)
    M0 = solve(bc_M - BMD.subs("x", bc_x).rhs)[0]
    if not type(M0) == dict:
        M0 = {"C1":M0}
    BMD = BMD.subs(M0)


    # たわみ角を求める d^2y/dx^2 = dθ/dx = -M(x)/EI
    defl_angle = dsolve(
        Eq(Derivative(theta, x), -BMD.rhs/(E*I)),
        func=theta,
    )
    # 境界条件から積分定数を計算、代入 bc_θ = θ(bc_x)
    theta0 = solve(bc_theta - defl_angle.subs("x", bc_x).rhs)[0]
    if not type(theta0) == dict:
        theta0 = {"C1":theta0}
    defl_angle = defl_angle.subs(theta0)


    # たわみを求める dy/dx= θ(x)
    deflection = dsolve(
        Eq(Derivative(delta, x), defl_angle.rhs),
        func=delta,
    )
    # 境界条件から積分定数を計算、代入 bc_δ = δ(bc_x)
    delta0 = solve(bc_delta - deflection.subs("x", bc_x).rhs)[0]
    if not type(delta0) == dict:
        delta0 = {"C1":delta0}
    deflection = deflection.subs(delta0)

    return SFD, BMD, defl_angle, deflection



print("一つ目")
node_0 = {
    "x":0,
    "F":symbols("R0"),
    "M":0,
    "θ":symbols("θ0"),
    "δ":0,
}
edge_01 = {
    "l":symbols("l1"),
    "q":0,
}
SFD01, BMD01, defl_angle01, deflection01 = generate_formulae(
    q=edge_01["q"],
    bc_x=node_0["x"],
    bc_F=node_0["F"],
    bc_M=node_0["M"],
    bc_theta=node_0["θ"],
    bc_delta=node_0["δ"],
)
pprint(SFD01)
pprint(BMD01)
pprint(defl_angle01)
pprint(deflection01)


print("二つ目")
node_1 = {
    "x":node_0["x"] + edge_01["l"],
    "F":-1*symbols("P"),
    "M":0,
    "θ":0,
    "δ":0,
}
edge_12 = {
    "l":symbols("l2"),
    "q":0,
}

bc_x = node_1["x"]
SFD12, BMD12, defl_angle12, deflection12 = generate_formulae(
    q=edge_12["q"],
    bc_x=bc_x,
    bc_F=SFD01.subs("x", bc_x).rhs + node_1["F"],
    bc_M=BMD01.subs("x", bc_x).rhs + node_1["M"],
    bc_theta=defl_angle01.subs("x", bc_x).rhs + node_1["θ"],
    bc_delta=deflection01.subs("x", bc_x).rhs + node_1["δ"],
)
pprint(SFD12)
pprint(BMD12)
pprint(defl_angle12)
pprint(deflection12)

print("最後の点")
node_2 = {
    "x":node_1["x"] + edge_12["l"],
    "F":symbols("R2"),
    "M":0,
    "θ":symbols("02"),
    "δ":0,
}

bc_x = node_2["x"]
# 力のつり合いとモーメントのつりあいの連立方程式
sigmaF = SFD12.subs("x", bc_x).rhs + node_2["F"]
sigmaM = BMD12.subs("x", bc_x).rhs + node_2["M"]
sigmatheta = defl_angle12.subs("x", bc_x).rhs + node_2["θ"]
sigmadelta = deflection12.subs("x", bc_x).rhs + node_2["δ"]
# 具体値を入れて計算
values = {
    "P":100,
    "l1":1,
    "l2":1,
    "E":206*10**9,
    "I":380*10**-12,
}
simultaneous_equations = [
    sigmaF.subs(values),
    sigmaM.subs(values),
    sigmatheta.subs(values),
    sigmadelta.subs(values),
]
# 解く
reaction_force = solve(simultaneous_equations)
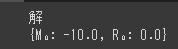
print("解")
pprint(reaction_force)


"""描画フェーズ"""
solutions = [
    [SFD01.subs(values).subs(reaction_force),  SFD12.subs(values).subs(reaction_force)],
    [BMD01.subs(values).subs(reaction_force),  BMD12.subs(values).subs(reaction_force)],
    [defl_angle01.subs(values).subs(reaction_force),  defl_angle12.subs(values).subs(reaction_force)],
    [deflection01.subs(values).subs(reaction_force),  deflection12.subs(values).subs(reaction_force)],
]

# グラフの描画
fig, axs = plt.subplots(4, 1, figsize=(6, 12))

# 各式をプロット
for i, solution in enumerate(solutions):
    x_values = [
        np.linspace(                       0, float(node_1["x"].subs(values)), 50),
        np.linspace(float(node_1["x"].subs(values)), float(node_2["x"].subs(values)), 50)
    ]
    # 梁の左右の分２回処理
    for j in range(len(x_values)):
        # 解をNumPy関数に変換
        expr = solution[j].rhs
        expr_numpy = lambdify(symbols("x"), expr, "numpy")

        # 描画
        if type(expr_numpy(x_values[j])) == float: # 定数式のとき
            axs[i].plot(x_values[j], expr*np.ones_like(x_values[j]), label=f'Equation {i+1}')
        else:
            axs[i].plot(x_values[j], expr_numpy(x_values[j]), label=f'Equation {i+1}')
        axs[i].axhline(0, color='black', linewidth=0.8, linestyle='--')
        axs[i].legend()
# 梁たわみ反転
axs[3].invert_yaxis()

# グラフの表示
plt.show()