材力の梁シミュレータを作る

概要

材料力学の梁を学ぶ際、SFDやらBMDやら出てきて計算がミスりやすかったり、本当に合ってるか分からず進んだりした経験がありました。
　全部積分してしまえば求まるはずなのに、面倒だと思っていたので、試しに片持ち梁の解析プログラムを作ってみました。
　参考になれば幸いです。

シミュレーション概要

BMDやSFD,たわみ角、たわみは以下のように、積分や微分方程式で対応付けできます。(初期条件や境界条件の扱いが大変ですが…)

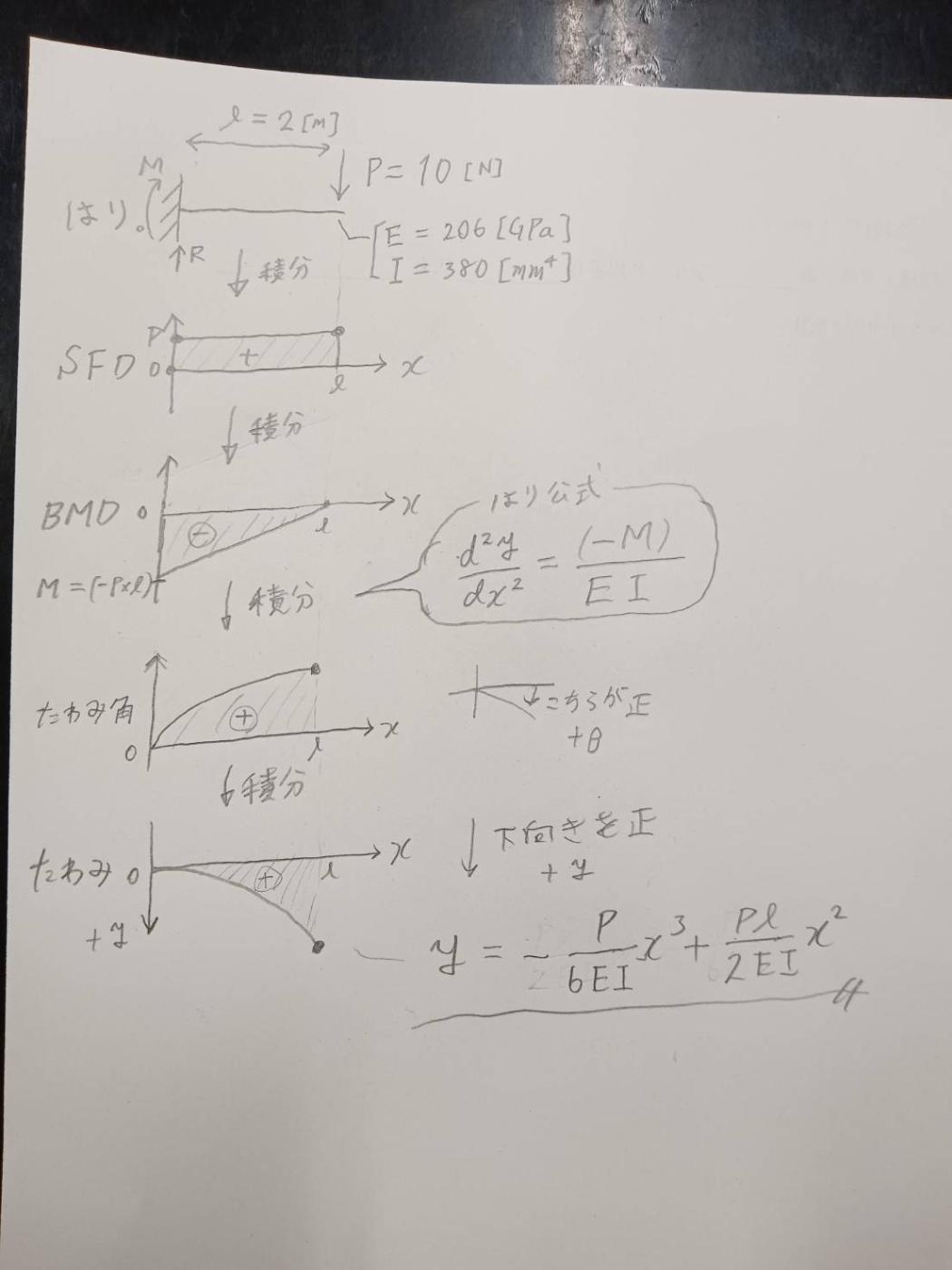
結果

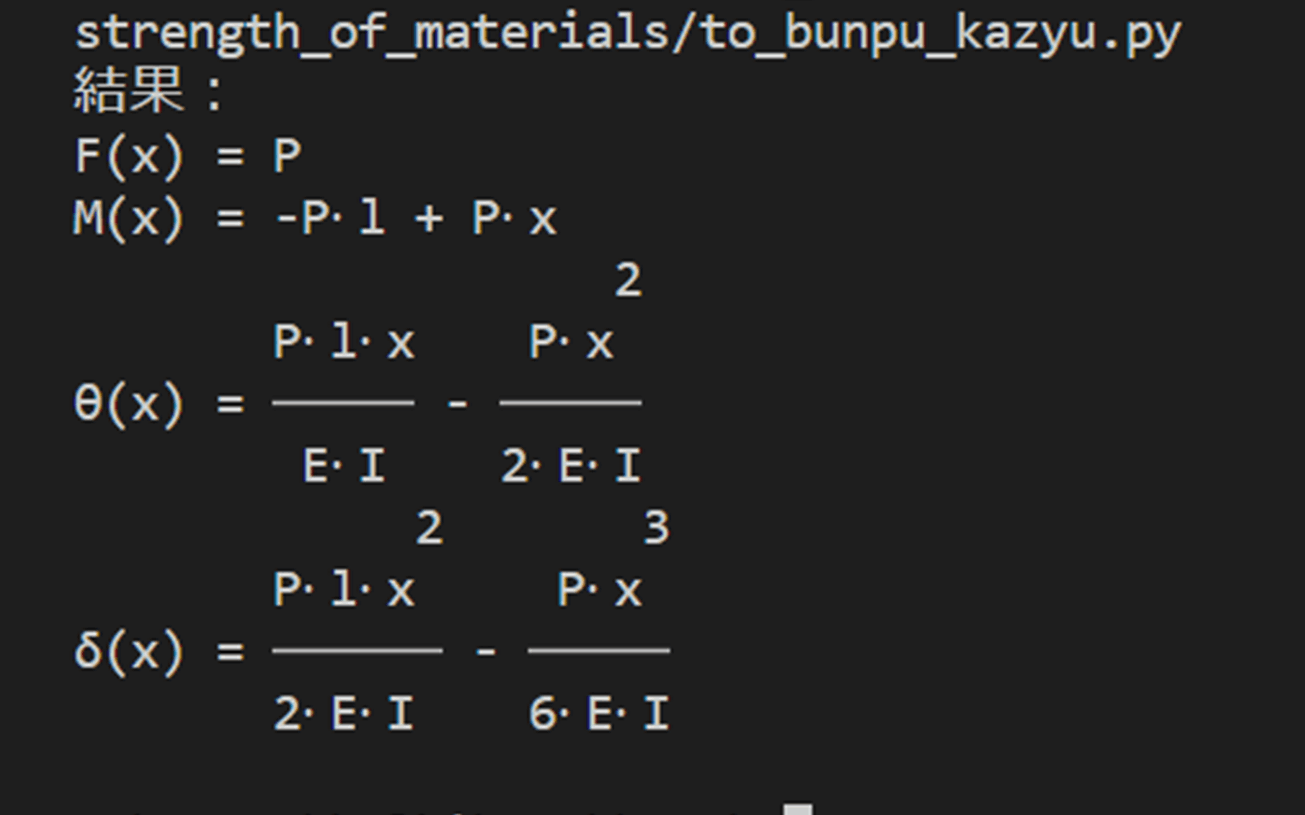
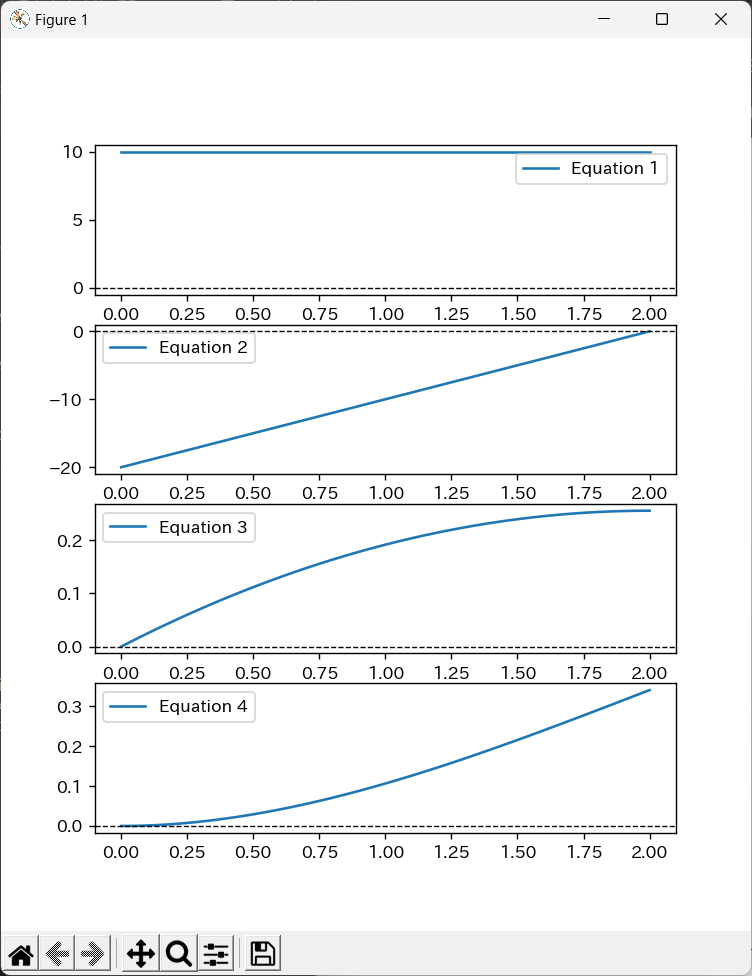
プログラム

pythonのsympy, matplotlibで作ってます

to_bunpu_kazyu.py

from sympy import pprint, Function, dsolve, Eq, Derivative, symbols, lambdify
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np


x = symbols('x')
E, I, q = symbols('E I q')
F = Function('F')(x)
M = Function('M')(x)
theta = Function('θ')(x)
D = Function('δ')(x)

# SFDを求める微分方程式 dF(x)/dx = 0 = 等分布荷重なし
SFD = dsolve(
    Eq(Derivative(F, x), 0),
    func=F,
    # ics={F.subs(x, )}
)
SFD = SFD.subs("C1", "P") # 初期条件の荷重代入

# BMDを求める微分方程式 dM(x)/dx = F(x)
BMD = dsolve(
    Eq(Derivative(M, x), SFD.rhs),
    func=M,
    # ics={M.subs(x, )}
)
BMD = BMD.subs("C1", "-P*l") # モーメント：M=P*l

# たわみ角を求める d^2y/dx^2 = dθ/dx = -M(x)/EI
deflection_angle = dsolve(
    Eq(Derivative(theta, x), -BMD.rhs/(E*I)),
    func=theta,
    # ics={M.subs(x, )}
)
deflection_angle = deflection_angle.subs("C1", 0) # 固定端のたわみ角はゼロ

# たわみを求める dy/dx= θ(x)
deflection = dsolve(
    Eq(Derivative(D, x), deflection_angle.rhs),
    func=D,
    # ics={M.subs(x, )}
)
deflection = deflection.subs("C1", 0) # 固定端のたわみはゼロ

print("結果：")
pprint(SFD)
pprint(BMD)
pprint(deflection_angle)
pprint(deflection)


"""描画フェーズ"""
length = 2
P = 10
E = 206*10**9
I = 380*10**-12

# 代入しつつまとめる
solutions = [
    SFD.subs("P", P),
    BMD.subs("P", P).subs("l", length),
    deflection_angle.subs("P", P).subs("l", length).subs("E", E).subs("I", I),
    deflection.subs("P", P).subs("l", length).subs("E", E).subs("I", I)
]

# グラフの描画
fig, axs = plt.subplots(4, 1, figsize=(6, 12))

# 各式をプロット
for i, solution in enumerate(solutions):
    # 解をNumPy関数に変換
    expr = solution.rhs
    expr_numpy = lambdify(x, expr, "numpy")
    # グラフの描画
    x_vals = np.linspace(0, length, 100)

    if type(expr_numpy(x_vals)) == int: # 定数式のとき
        axs[i].plot(x_vals, expr*np.ones_like(x_vals), label=f'Equation {i+1}')
    else:
        axs[i].plot(x_vals, expr_numpy(x_vals), label=f'Equation {i+1}')
    axs[i].axhline(0, color='black', linewidth=0.8, linestyle='--')
    axs[i].legend()

# グラフの表示
plt.show()

理解の補助(二階微分方程式をsympyで段階的に解く)

StepwiseSecondOrderDifferentialEquation.py

from sympy import pprint, Function, dsolve, Eq, Derivative, symbols

# 変数と未知関数の定義
x = symbols('x')
y = Function("y")(x)
# 一階微分：dy/dx
dy_dx = Function('dy/dx')(x)

# 二階微分方程式をdy/dxで一階微分方程式として作る
# d2y/dx2=x
eq1 = Eq(Derivative(dy_dx, x), x)
# 解く
dy_dx_sol = dsolve(
    eq1,
    func=dy_dx,
    # ics={dy_dx.subs(x, 0): 0} # 初期条件
)

# 得られた解を使って二階微分方程式を再構築
eq2 = Eq(Derivative(y, x), dy_dx_sol.rhs)
# 解く
y_sol = dsolve(
    eq2,
    func=y,
    # ics={y.subs(x, 0): 0}
)

pprint(y_sol)

今後について

sympyの扱いやすさにびっくりしました。
もっと一般化してみたいのですが、場合分けがなかなかしんどいので現在作成中です。

中身が理解できる方は他の問題でもやってみてください。
ありがとうございました。