🐥

ロジスティック方程式 (人口増加モデル)を解く

2023/06/09に公開

Julia

tech

謝辞: 石田洋音、坂上滉太朗

問題設定

微分方程式

$\dfrac{dN(t)}{dt} = rN(t)\left(1- \dfrac{N(t)}{K}\right)$

$K$ は環境の収容能力、 $r$ は人口の成長率を表す。

初期条件

$N\left(t_0\right)=N_0=1.0\quad\dots\quad\left(2\right)$

解析解

$N\left(t\right)=\dfrac{K}{1 + \left(\dfrac{K}{N_0}-1\right)e^{-rt}}$

プロジェクト環境の作成

グローバル環境で作業しても良いのですが、折角これまでの記事でプロジェクト環境を学んだので、活用してみましょう。

$ cd ~workspace

julia> using Pkg
julia> Pkg.generate("logistic")
  Generating  project logistic:
    logistic/Project.toml
    logistic/src/logistic.jl
Dict{String, Base.UUID} with 1 entry:
  "logistic" => UUID("c3e47827-092d-47ff-a424-38e9f9494d2c")
(@v1.9) pkg> activate logistic # logisticプロジェクトを有効化
  Activating project at `~/workspace/logistic`
(logistic) pkg> add Plots # Plotsを依存性に追加

オイラー法による解法

それでは一番単純 (ただし精度は良くない)オイラー方程式での解法を試してみましょう。
オイラー法では、時刻の刻み幅 $h$ に対して、
$N(t + h) \simeq N(t) + \dfrac{dN(t)}{dt}\Big|_t \times h + O(h^2)$
と近似します。この操作を繰り返すことで、 $N(t)$ の時間発展を離散的なグリッドの上で計算できます。

では、~workspace/logistic以下に移動し、notebook/logistic.ipynbファイルを作成します。

$ mkdir notebook
$ touch notebook/logistic.ipynb

VS CodeのJupyter extensionを使ってこのファイルを開き、環境としてlogisticプロジェクト環境を選びましょう。

まず最初に、 $N(t)$ の導関数を計算するderiv_Nt、それを使って次の時刻の $N(t)$ を計算するnext_Nt関数を定義します。

# Compute the derivative of N(t)
deriv_Nt(nt, K, r) = r*nt*(1-nt/K)

# Compute N(t + h)
next_Nt(nt, K, r, h) = nt + h*deriv_Nt(nt, K, r)

(必要に応じて、コメントを付けましょう!)
これらの関数は、必要なパラメータ $K$ , $r$ 等を引数経由で受け取ります。グローバル変数を使わないのは、型安定性を保障するためです。

次のセルで、グローバル変数としてパラメータを設定します。

# 各種パラメータを定義
tmax = 10.0 # 終了時刻
r = 1.0 # パラメータ1
K = 10.0 #パラメータ2
N0 = 1.0 # 人口の初期値
numtimes  = 100 # 0 ≦ t < tmaxの分割数

h = tmax/numtimes

気になる場合、以下の様に@code_warntypeマクロを使って、グローバル変数が混入していないか、確認できます。(混入している場合、Any型の変数が現れます)

# 型安定性のチェック
@code_warntype deriv_Nt(N0, K, r)

@code_warntype next_Nt(N0, K, r, h)

これらの関数を使って、時間発展を計算してみましょう。

results = Vector{Float64}(undef, numtimes+1)

# 初期値
results[1] = N0

# 時間発展
for t in 1:numtimes
    results[t+1] = next_Nt(results[t], K, r, h)
end

0から $t_\mathrm{max}$ まで、numtimes+1個のグリッド上で計算された $N(t)$ の値が、resultsに1次元配列として格納されているはずです。

Plots.jlを使ってプロットしてみましょう。

using Plots

times = LinRange(0, tmax, numtimes+1)

plot(times, results, label="Numerical", xlabel="time")

精度を確認するため、解析的な解を数値的に評価した値と比べてみます。
そのために、ある時刻timeでの厳密解を評価する関数exact_Ntを先ず定義します。
ここで、 $K$ , $r$ をグローバル変数経由で渡していますが、計算は一瞬なので気にしないことにします。
この関数をJuliaのブロードキャストを使って、times配列の全ての要素に適用します。

exact_Nt(time) = K/(1+(K-N0) / N0 * exp(-r*time))

p = plot(yaxis=:log, ylims=(1e-10, 1000),  xlabel="time")
plot!(p, times, results, label="Numerical")
plot!(p, times, abs.(results .- exact_Nt.(times)), marker=:x, label="Error")

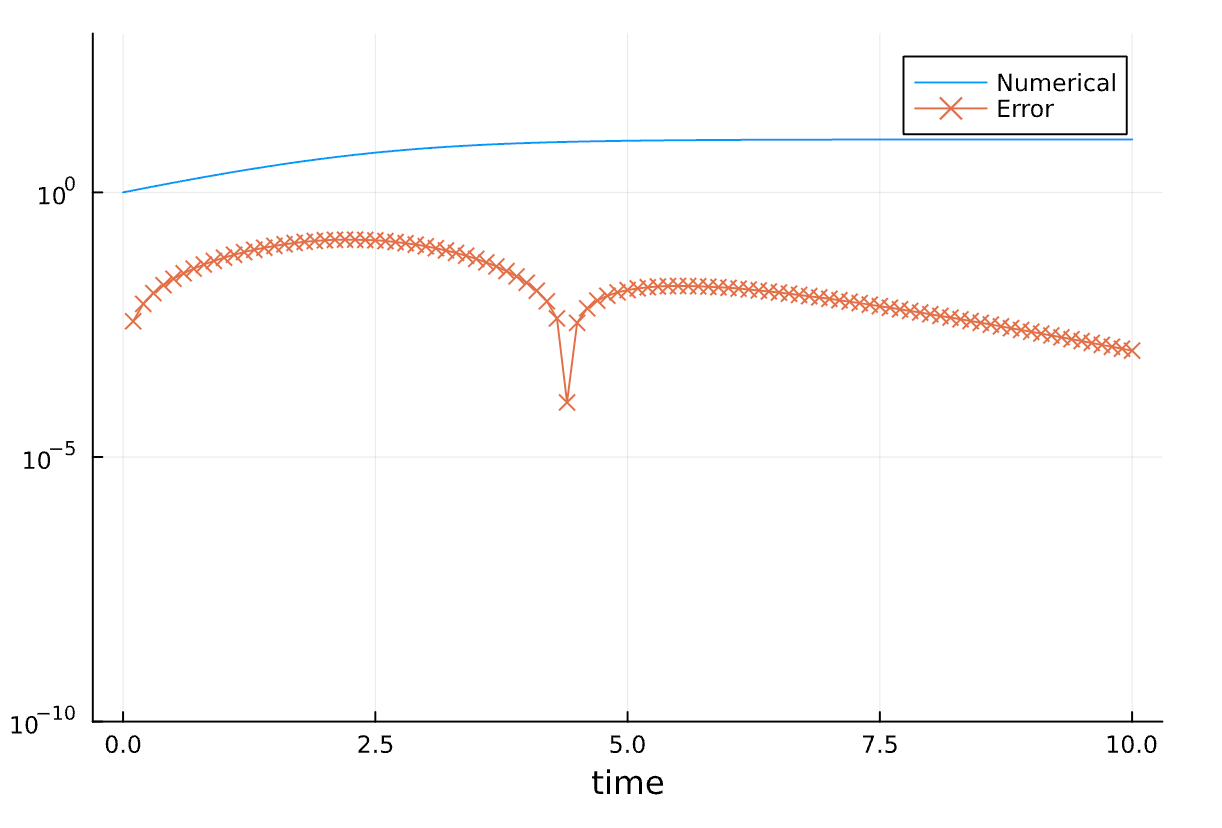
2桁ぐらいの精度はでていますね。では、以下ではもっと精度の良い手法を使って解いてみましょう。

DifferentialEquations.jlを利用

ここでは、微分方程式の数値解法を集めた有名なライブラリDifferentialEquations.jlを使ってみます。まずは、プロジェクト環境に導入しましょう。

(logistic) pkg> add DifferentialEquations
   Resolving package versions...
   Installed SciMLNLSolve ────────────── v0.1.7
   Installed DiffEqBase ──────────────── v6.125.1
   Installed NonlinearSolve ──────────── v1.8.0

次に、ノートブックの続きに以下の様に入力すると、5次のルンゲクッタ法を使って解くことが出来ます。

using DifferentialEquations

# ロジスティック方程式の定義
function logistic!(du, u, params, t)
    r, K = params
    du[1] = r * u[1] * (1 - u[1]/K)
end

# パラメータの設定
params = (r, K)

# 初期条件の設定
u0 = [1.0]  # 開始時点の人口サイズ

# 時間範囲の設定
tspan = (0.0, tmax)

# 問題の設定
prob = ODEProblem(logistic!, u0, tspan, params)

# 微分方程式の解 (5次のルンゲクッタ法)
sol = solve(prob, Tsit5(), abstol=1e-8, reltol=1e-8)
;

# 解のプロット

results_de = [u_[1] for u_ in sol.u]

p = plot(yaxis=:log, ylims=(1e-10, 1000),  xlabel="time")
plot!(p, sol.t, results_de, marker=:o)
plot!(p, sol.t, abs.(results_de .- exact_Nt.(sol.t)), label="error")

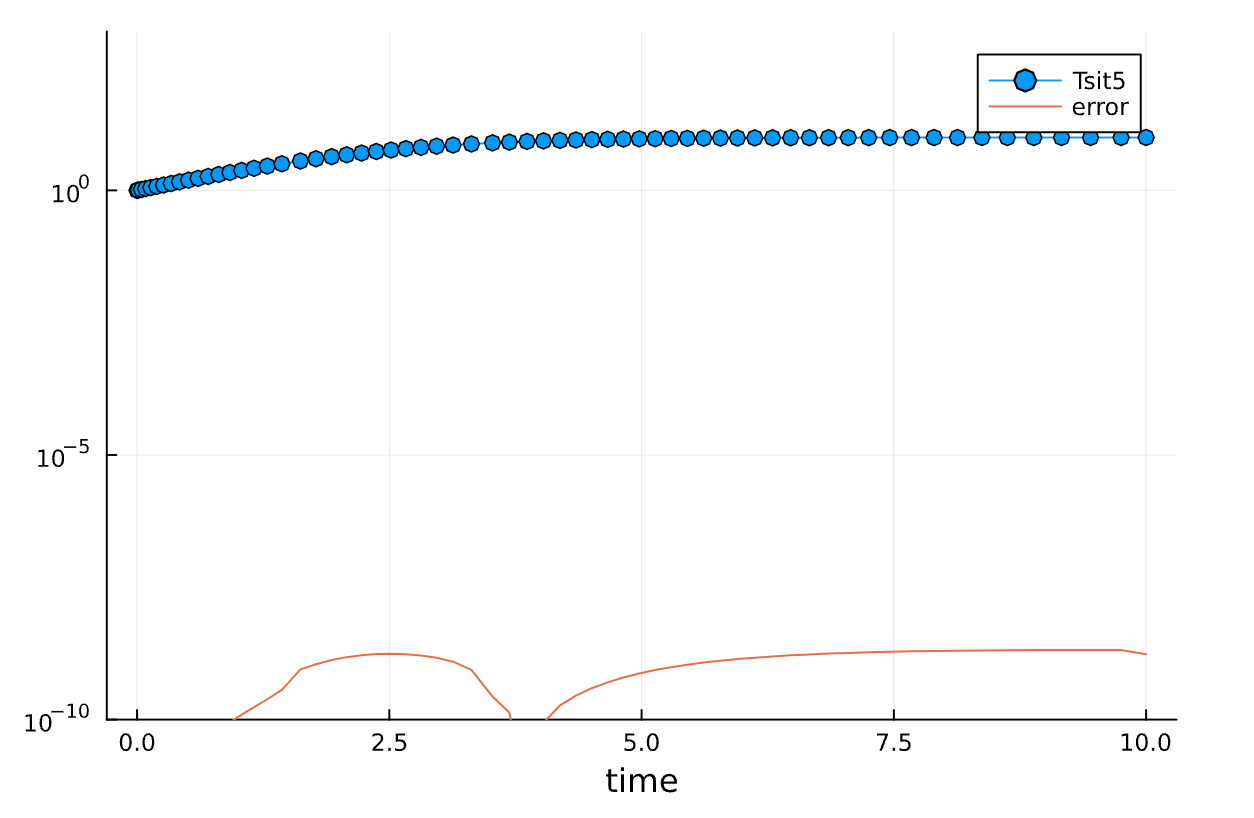
どうでしょうか？劇的に精度が改善されました。

演習問題

以上で作成したプロジェクトをGitHub上のpublic repositoryにアップロードしてみましょう。
ただし、ノートブックを保存する際、出力・計算結果を消去しておくと、Gitによるバージョン管理が楽になります。