オブジェクトのScale値を取得する関数はありますが(「ObjectScale」ノード)、オブジェクトのRotation値を取得する関数はなかったので、自作してみました。

結果動画
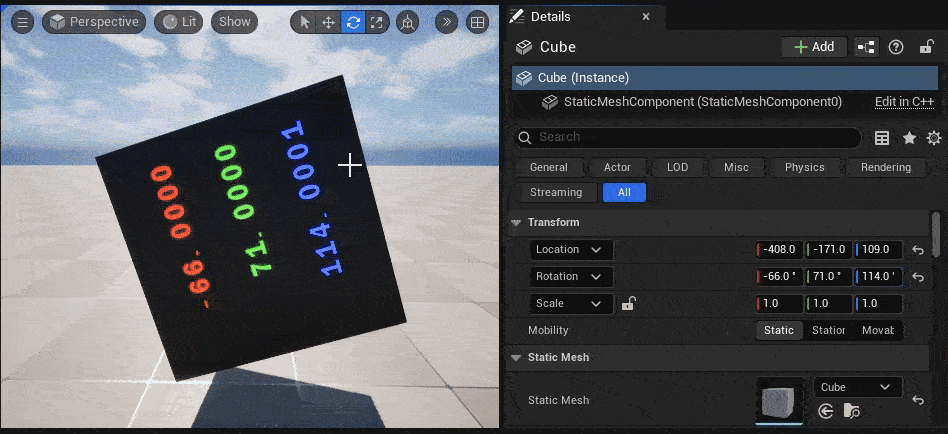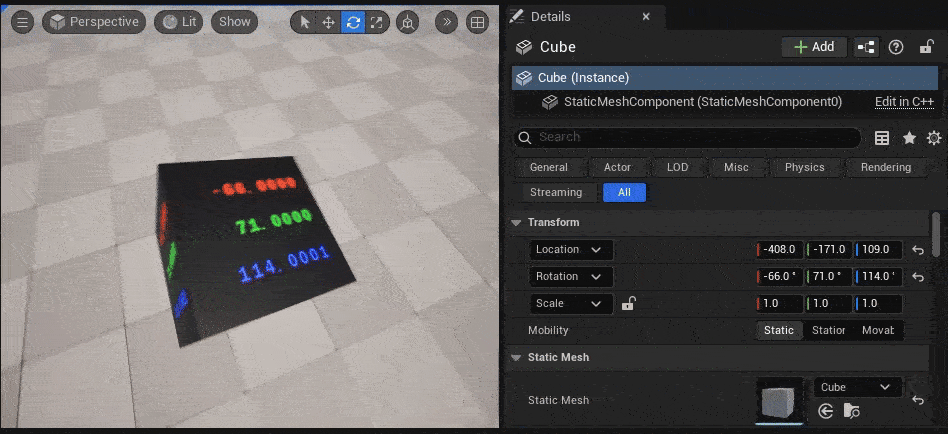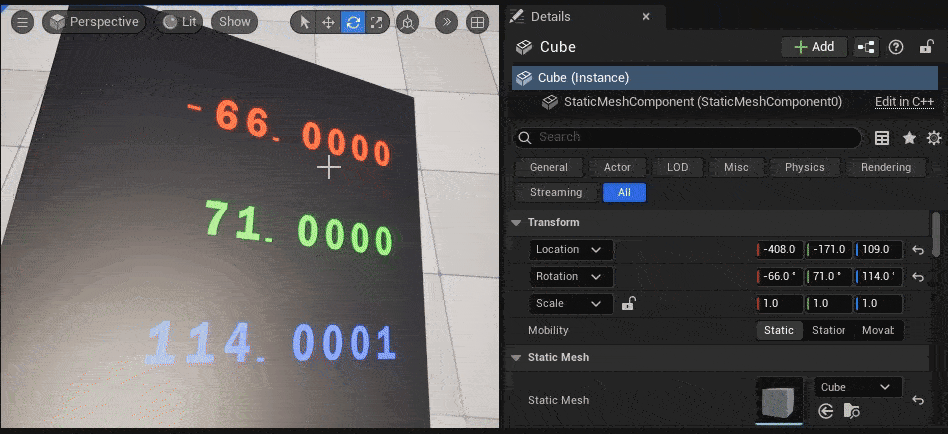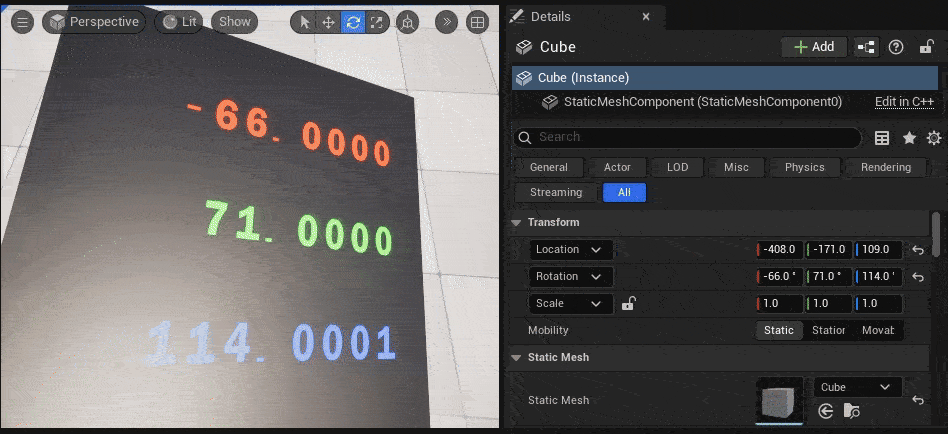
今回自作したMF_ObjectRotationのノードの返り値である float3(x=Roll, y=Pitch, z=Yaw) を、「DebugFloat3Values」ノードで可視化してみます。

↓のGIF動画のように、TransformのRotationに入力した値(= Cubeにかけた回転値)と同じ値が、オブジェクト表面に表示されています。
| No |
GIF |
| 1 |
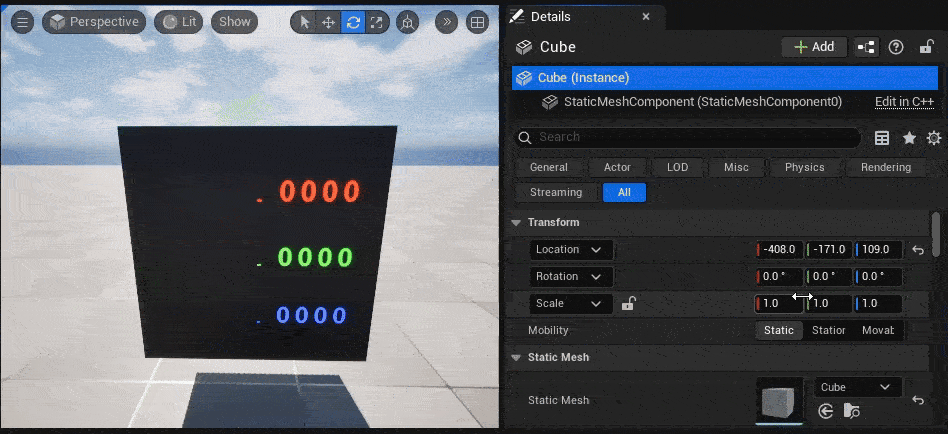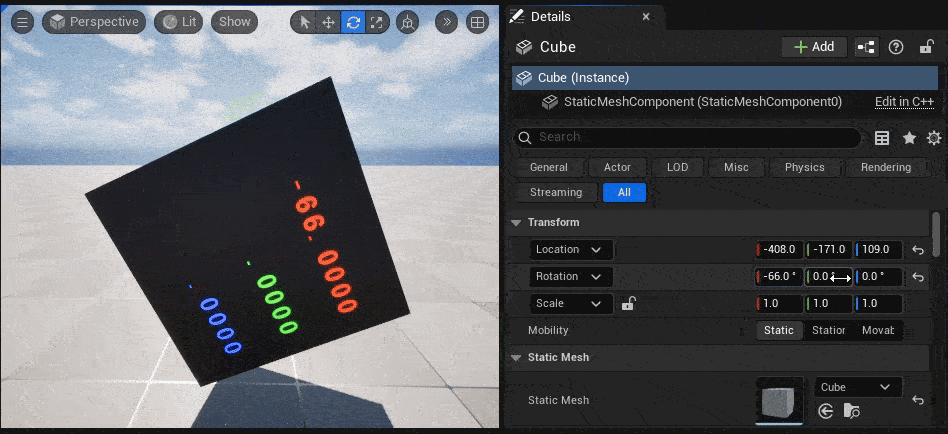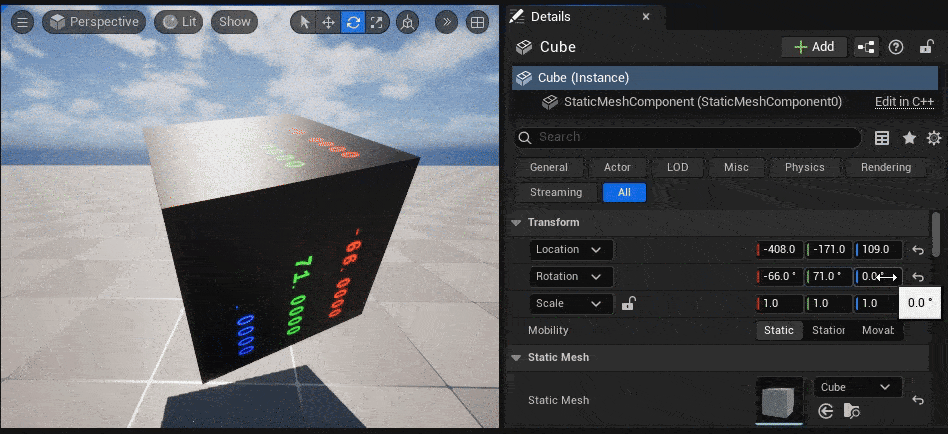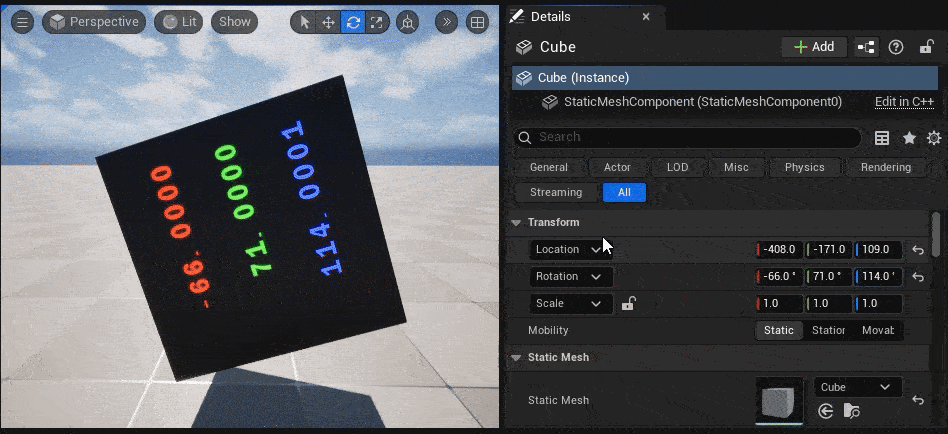 |
| 2 |
 |
全体図
こちらが今回自作したMF_ObjectRotationノードの全体図です。

コアの部分はCustomノードで、HLSLで書いています。
float pitchRad = asin(ForwardVec.z);
float pitch = degrees(pitchRad);
float roll = 0.0f;
float yaw = 0.0f;
if (cos(pitchRad) != 0.0f)
{
float rollRad = atan2(-RightVec.z, UpVec.z);
roll = degrees(rollRad);
float yawRad = atan2(ForwardVec.y, ForwardVec.x);
yaw = degrees(yawRad);
}
else
{
roll = 0.0f;
float yawRad = atan2(-RightVec.x, RightVec.y);
yaw = degrees(yawRad);
}
return float3(roll, pitch, yaw);
解説
最初に、オブジェクトにかかっているTransformから、カスタム座標系を算出します。

カスタム座標系からオイラー角を算出する式を構築
次に、カスタム座標系からオイラー角(Roll, Pitch, Yaw)を算出する式を構築します。
ここが今回の本丸部分になります。
まず、回転行列Rの各要素を次のように表すとします。
R =
\begin{bmatrix}
m_{00} & m_{01} & m_{02} \\
m_{10} & m_{11} & m_{12} \\
m_{20} & m_{21} & m_{22}
\end{bmatrix}
また、各軸が[Forward, Right, Up]のカスタム座標系は、行列の形では次のように表せます。
R =
\begin{bmatrix}
Forward.x & Right.x & Up.x \\
Forward.y & Right.y & Up.y \\
Forward.z & Right.z & Up.z
\end{bmatrix}
Roll, Pitch, Yawそれぞれの回転行列は次のようになります。
R_{Roll} =
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\theta_{Roll} & -\sin\theta_{Roll} \\
0 & \sin\theta_{Roll} & \cos\theta_{Roll}
\end{bmatrix}
R_{Pitch} =
\begin{bmatrix}
\cos\theta_{Pitch} & 0 & \sin\theta_{Pitch} \\
0 & 1 & 0 \\
-\sin\theta_{Pitch} & 0 & \cos\theta_{Pitch}
\end{bmatrix}
R_{Yaw} =
\begin{bmatrix}
\cos\theta_{Yaw} & -\sin\theta_{Yaw} & 0 \\
\sin\theta_{Yaw} & \cos\theta_{Yaw} & 0 \\
0 & 0 & 1
\end{bmatrix}
オイラー角では回転順が最終結果に影響します。
UnrealEngineではRoll, Pitch, Yawの順で回転がかけられますが、これは
Yaw → Pitch → Roll
のように左からかけるので、合成後の回転行列は
R_{Yaw}R_{Pitch}R_{Roll}
で求まります。
R_{Yaw,Pitch,Roll} =
\begin{bmatrix}
\cos\theta_{Pitch}\cos\theta_{Yaw} & \sin\theta_{Roll}\sin\theta_{Pitch}\cos\theta_{Yaw} - \cos\theta_{Roll}\sin\theta_{Yaw} & \cos\theta_{Roll}\sin\theta_{Pitch}\cos\theta_{Yaw} + \sin\theta_{Roll}\sin\theta_{Yaw} \\
\cos\theta_{Pitch}\sin\theta_{Yaw} & \sin\theta_{Roll}\sin\theta_{Pitch}\sin\theta_{Yaw} + \cos\theta_{Roll}\cos\theta_{Yaw} & \cos\theta_{Roll}\sin\theta_{Pitch}\sin\theta_{Yaw} -\sin\theta_{Roll}\cos\theta_{Yaw} \\
-\sin\theta_{Pitch} & \sin\theta_{Roll}\cos\theta_{Pitch} & \cos\theta_{Roll}\cos\theta_{Pitch}
\end{bmatrix}
上記より、
m_{20} = Forward.z = -\sin\theta_{Pitch}
★ \enspace \theta_{Pitch} = \arcsin(-Forward.z)
となり、まずPitchが求まります。
続いて、RollとUpを求めますが、\cos\theta_{Pitch} \neq 0 のときと、\cos\theta_{Pitch} = 0 のときで場合分けします。
まず、\cos\theta_{Pitch} \neq 0 のとき
m_{21} = Right.z = \sin\theta_{Roll}\cos\theta_{Pitch} \\
\sin\theta_{Roll} = \frac{Right.z}{\cos\theta_{Pitch}}
m_{22} = Up.z = \cos\theta_{Roll}\cos\theta_{Pitch} \\
\cos\theta_{Roll} = \frac{Up.z}{\cos\theta_{Pitch}}
より、
\frac{\sin\theta_{Roll}}{\cos\theta_{Roll}} = \tan\theta_{Roll} = \frac{Right.z}{Up.z}
★ \enspace \theta_{Roll} = \arctan(\frac{Right.z}{Up.z})
で、Rollが求まります。
また、
m_{10} = Forward.y = \cos\theta_{Pitch}\sin\theta_{Yaw} \\
\sin\theta_{Yaw} = \frac{Forward.y}{\cos\theta_{Pitch}}
m_{00} = Forward.x = \cos\theta_{Pitch}\cos\theta_{Yaw} \\
\cos\theta_{Yaw} = \frac{Forward.x}{\cos\theta_{Pitch}}
より、
\frac{\sin\theta_{Yaw}}{\cos\theta_{Yaw}} = \tan\theta_{Yaw} = \frac{Forward.y}{Forward.x}
★ \enspace \theta_{Yaw} = \arctan(\frac{Forward.y}{Forward.x})
で、Yawが求まります。
次に、\cos\theta_{Pitch} = 0 のとき
このときはジンバルロックが発生してForward軸とUp軸の回転が同軸での回転となります。
ここで、\theta_{Roll} = 0 と仮定(すなわち、\sin\theta_{Roll} = 0、\cos\theta_{Roll} = 1)すると、回転行列は、
R_{Yaw,Pitch,Roll} =
\begin{bmatrix}
0 & -\sin\theta_{Yaw} & \sin\theta_{Pitch}\cos\theta_{Yaw} \\
0 & \cos\theta_{Yaw} & \sin\theta_{Pitch}\sin\theta_{Yaw} \\
-\sin\theta_{Pitch} & 0 & 0
\end{bmatrix}
となります。
ここから、
\tan\theta_{Yaw} = \frac{\sin\theta_{Yaw}}{\cos\theta_{Yaw}} = -\frac{m_{01}}{m_{11}} = -\frac{Right.x}{Right.y}
★ \enspace \theta_{Yaw} = \arctan(-\frac{Right.x}{Right.y})
で、Yawが求まります。
以上より、
\begin{aligned}
&\theta_{Roll} =
\begin{cases}
\arctan(\frac{Right.z}{Up.z}) &\text{} (\cos\theta_{Pitch} \neq 0) \\
0 &\text{} (\cos\theta_{Pitch} = 0)
\end{cases} \\
&\theta_{Pitch} = \arcsin(-Forward.z) \\
&\theta_{Yaw} =
\begin{cases}
\arctan(\frac{Forward.y}{Forward.x}) &\text{} (\cos\theta_{Pitch} \neq 0) \\
\arctan(-\frac{Right.x}{Right.y}) &\text{} (\cos\theta_{Pitch} = 0)
\end{cases} \\
\end{aligned}
CustomノードでHLSLの記述
上記までで求めたカスタム座標系とオイラー角算出の式を使って、オイラー角を返すCustomノードとしてHLSLコードを起こします。

Customノードの引数は、カスタム座標系のForwardベクトル、Rightベクトル、Upベクトルの3つです。
それら引数のベクトルをもとに、まずPitchから求めます。
RollとYawを求めるときには、ジンバルロックを考慮して、if (cos(pitchRad) != 0.0f)で場合分けします。
最終的には、float3(x=roll, y=pitch, z=yaw) として値を返しています。
参考ページ
回転行列⇔オイラー角の相互変換について、こちらのページを大いに参考にさせていただきました。
https://qiita.com/aa_debdeb/items/3d02e28fb9ebfa357eaf







Discussion