[UE5][Houdini][習作] Houdiniで頂点に仕込んだ情報を元に、UEのマテリアルでポリゴンの部分回転アニメ（ファイル配布）
前回の習作に続き、Houdini側でモデルの頂点に情報を仕込んで、その情報を元に、UEのマテリアルでWorldPositionOffsetによってポリゴンの部分回転アニメをしてみました。
【前回の習作】
デモムービー
こちらが作成したもののデモムービーになります。
【ポリゴン（Box）の部分回転の様子】
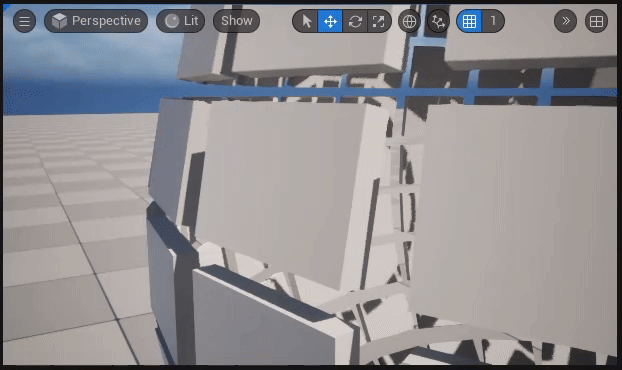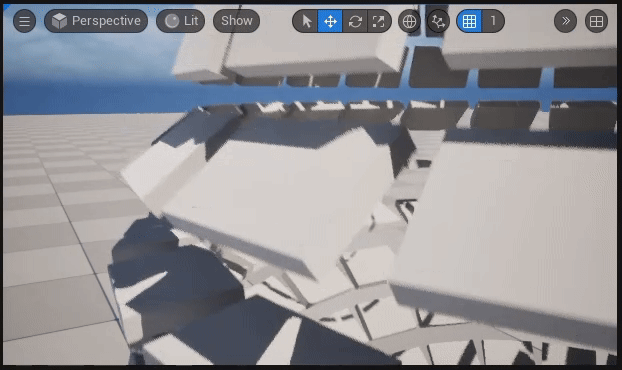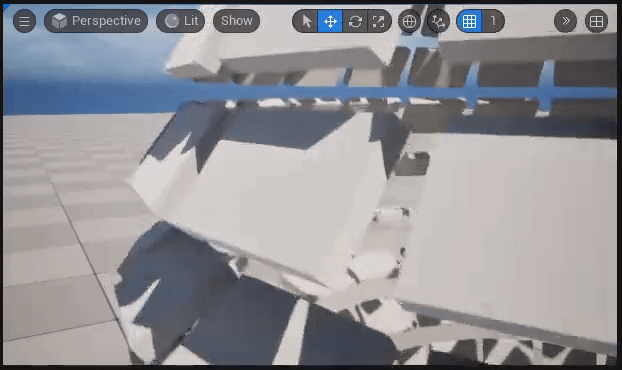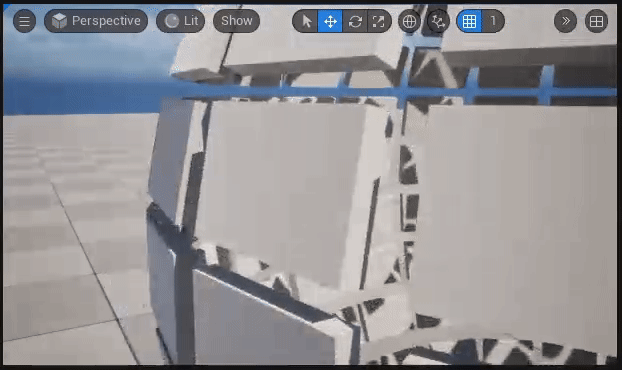
解説
[Houdini側] 基本形の作成
↓のような厚みを薄くしたBoxを、
↓のような極地（最上下点）を削除したShpereの面上に貼り付けるようにコピーします。
これには「Copy to Point」ノードを使います。
その際、コピー前にpscaleを上下端に向かうに連れ、小さくなるように設定しておきます。（そうしないとBoxが重なってしまうので。）
また、Boxが経緯線に沿って配置されるように、「up」ベクトルAttributeを作成しておきます。
青ベクトルがNormal、黄ベクトルがup
upベクトルの算出には、外積を使います。
vector worldUpVec = {0, 1, 0};
vector tangent = cross(@N, worldUpVec);
v@up= cross(tangent , @N);
想定通りコピーされると↓のようになります。
これを基本形として、頂点に必要な情報を仕込んでいきます。
[Houdini側] 仕込み情報：各Boxの重心点
各Boxは各々の重心点をピボットとして回転させますので、Boxの各頂点にその重心点の情報を仕込みます。
Boxの重心点は後から算出するより、コピー前に作っておくほうが楽です。Pivotを原点のままにしておけば重心点は当然(0,0,0)になります。ここでは「center」という名のAttributeで作成しています。
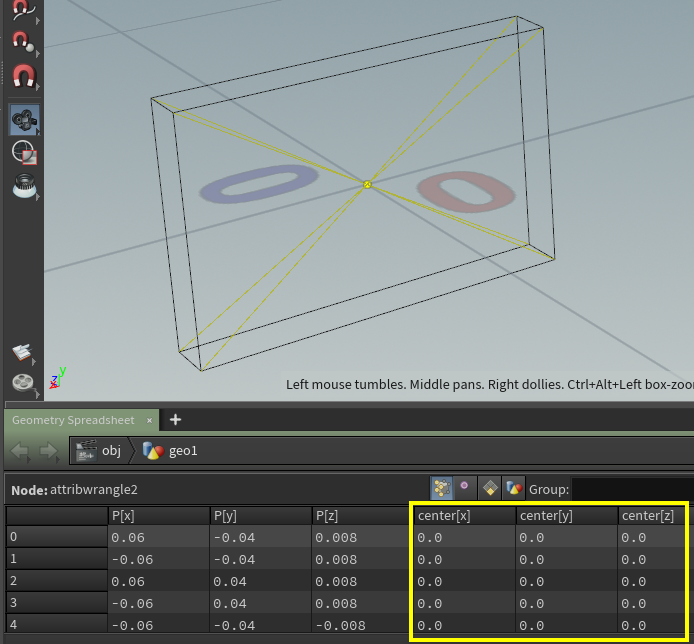黄色い点がBoxの重心点
「Copy to Point」ノードでコピーすれば、「center」Attributeにも自動的にTransformがかかり、欲しい情報が簡単に得られます。
黄色い点がBoxの重心点
注意点として、「center」AttributeにTransform(移動、回転、スケール)がかかるようにするには、metadataを"point"にしておく必要があります。
setattribtypeinfo(0, "point", "center", "point");
これについてはこちらのページで解説しておりますので、ぜひご覧ください。
最後に、「Attribute Promote」ノードで、「center」AttributeをPointクラスからVertexクラスに移します。
[Houdini側] 仕込み情報をUVに割り当てる
仕込み情報（重心点）はUEのマテリアル側で参照したい情報になりますので、これをUVに割り当てます。重心点は[3-Float]ですので、今回はuv3, uv4の2つを使います。
-
仕込み情報：重心点
- uv3.x、uv3.y、uv4.x、 の3つを使用。
ここでも注意点があります。
Houdini側でUVに割り当てた値は、UE側ではそのUVのV値がOneMinus（1-x）された値になってしまうので、uv3.yのみあらかじめOneMinus（1-x）した上でに格納しておきます。
@uv3.x = @center.x;
@uv3.y = 1.0 - @center.y;
@uv4.x = @center.z;
このことについては↓のページで解説しておりますので、ぜひご覧ください。
Houdini側の作業はここまでで、以上のモデルをFBXで書き出します。
[UE側] FBXをインポートする
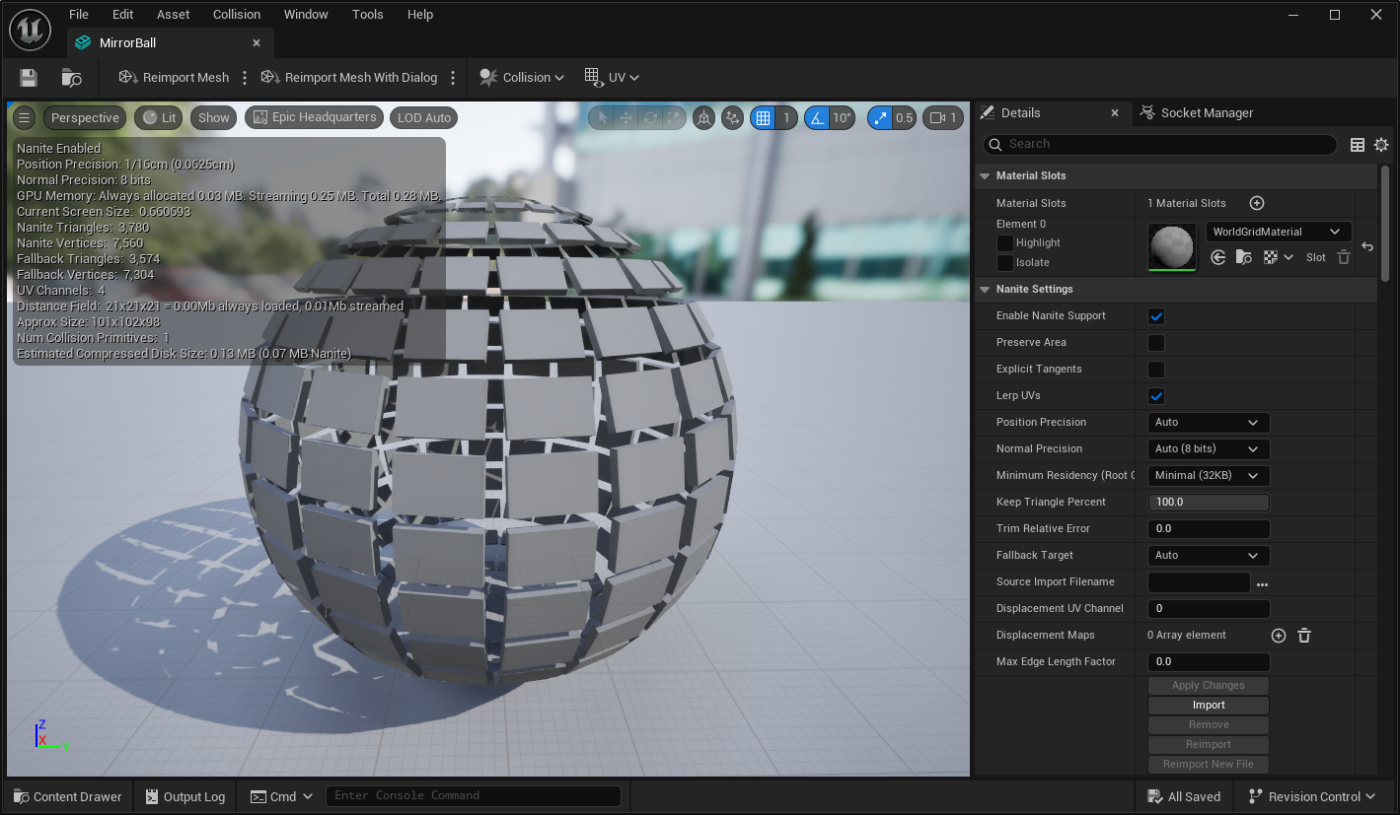
書き出したFBXをUEにインポートします。
その際、UniformScaleは100にしておきます。
[UE側] マテリアルを作成する
重要なポイントは、Houdini側でUVに仕込んだ情報を取り出すところになります。
「重心点」の情報
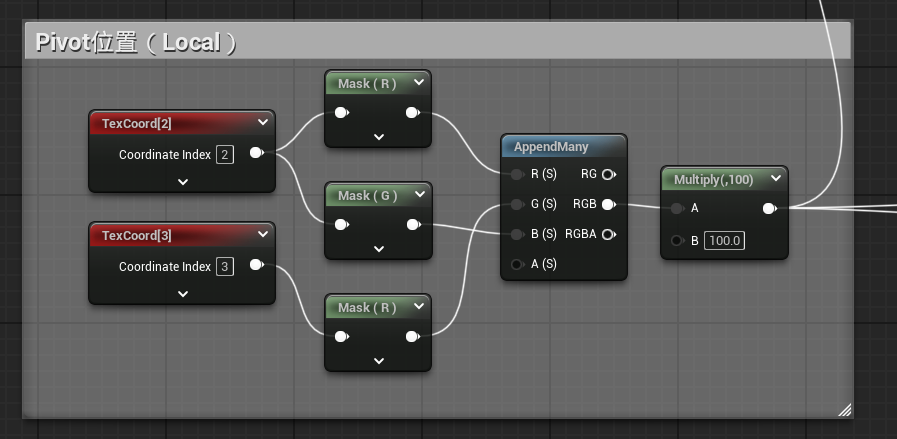
こちらはuv3.x、uv3.y、uv4.xに割り当てたので、UEマテリアルではそれぞれ [2].R、[2].G、[3].R に該当します。（ややこしいですが、インデックス番号のズレに注意します。）
[2].R、[2].G、[3].Rの3つをAppendして、「重心点」を復元してあげます。
注意点として、HoudiniとUEの座標系の違いから、YとZを入れ替えてあげる必要があります。なのでここでは [2].GをZに、[3].RをYに しています。
また、インポート時にUniformScaleを100にしたので、重心点にも100をかけてあげます。
BoxのLocal座標系の算出
「重心点」はLocal空間の値であり、オブジェクトの中心はSphereの中心と一致していますので、「重心点」の値がそのままBoxのLocal空間でのNormalベクトルとなります。それとUpベクトル(0,0,1)を補助ベクトルとして、BoxのLocal座標系たるカスタム直交座標を算出してあげます。この直交座標のY軸(Rightベクトル)がBoxの回転軸となります。
なお、↑で登場した「MF_MakeCoordSystemFromXZ」ノードは、「基準となるX軸と、補助となるZ軸を引数にして、両者が直交する座標軸を作成する」ノードです。
「MF_MakeCoordSystemFromXZ」ノードの中身
【返り値の説明】
- 「X」：入力の「BaseX」のまま正規ベクトルとして返ってきます。
- 「Y」：入力の「BaseX」と「OptionalZ」に直交する正規ベクトルとして返ってきます。
- 「Z」：「X」と「Y」に直交する正規ベクトルとして返ってきます。
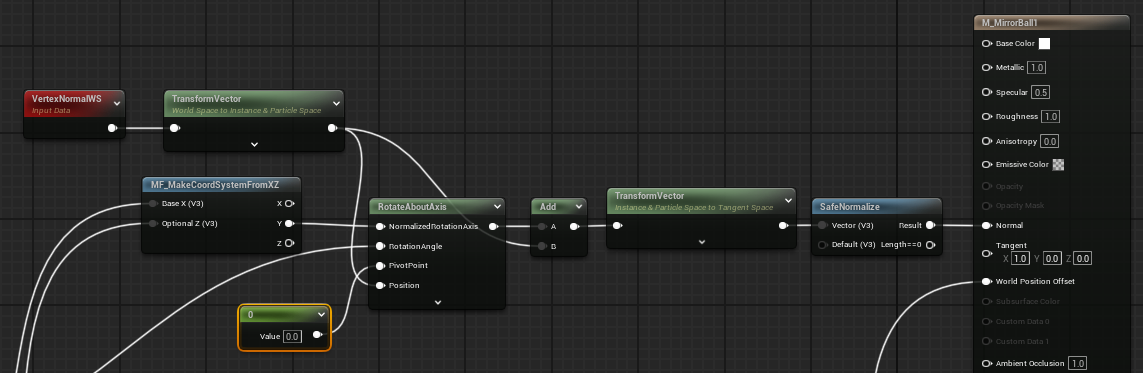
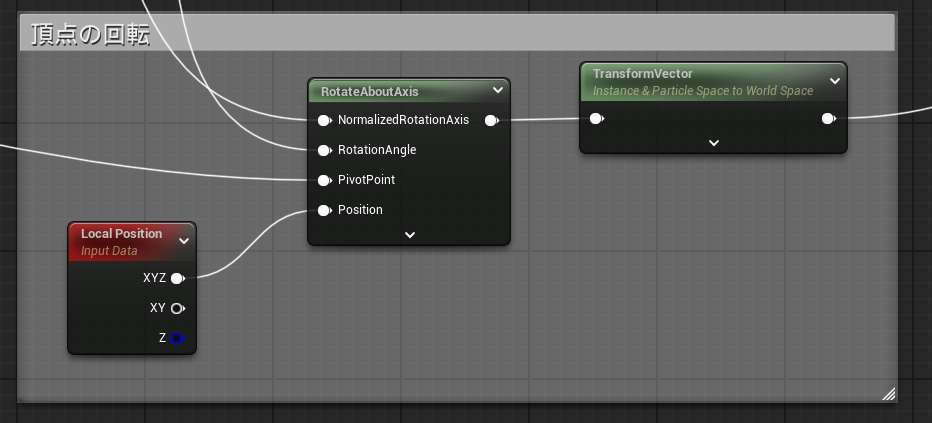
頂点と頂点Normalの回転
前述の回転軸で頂点を回転させます。留意点として、ここでやっていることはLocal空間での計算です。なので、「RotateAboutAxis」ノードの「Position」ピンにつなぐのは「LocalPosition」になります。算出した回転の差分はLocal空間のものですので、これを「TransformVector」ノードによってWorld空間に変換してメインマテリアルノードにつなぎます。
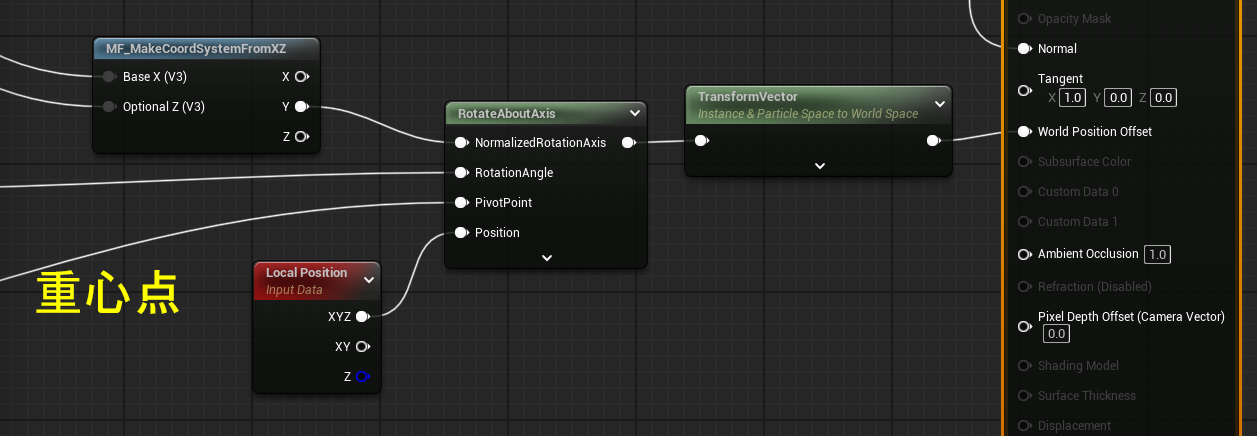
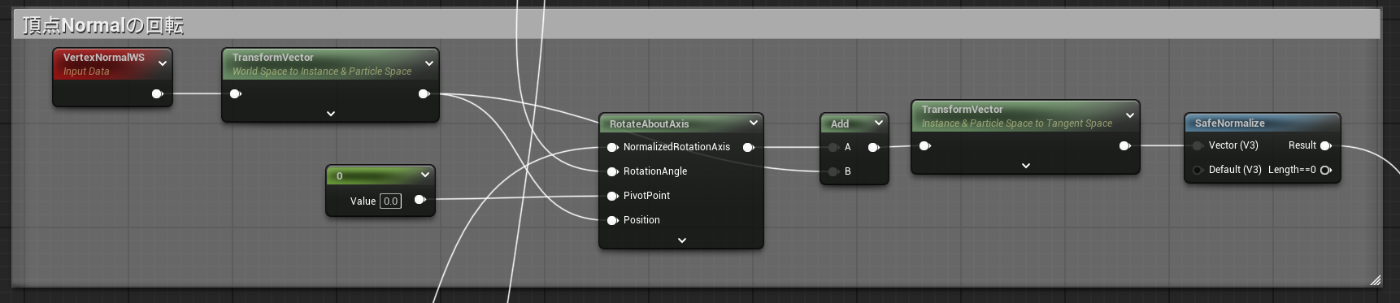
同様に、頂点Normalも回転させます。
回転軸がLocal空間のものですので、VertexNormalWSも一旦Local空間に変換したうえで、Local空間上で回転計算します。算出した新しいNormalは、頂点同様、World空間に変換してメインマテリアルノードにつなぎます。
なお、「RotateAboutAxis」ノードを使った頂点と頂点Normalの回転については↓のページで解説しておりますので、詳しく知りたい方はぜひご覧ください。
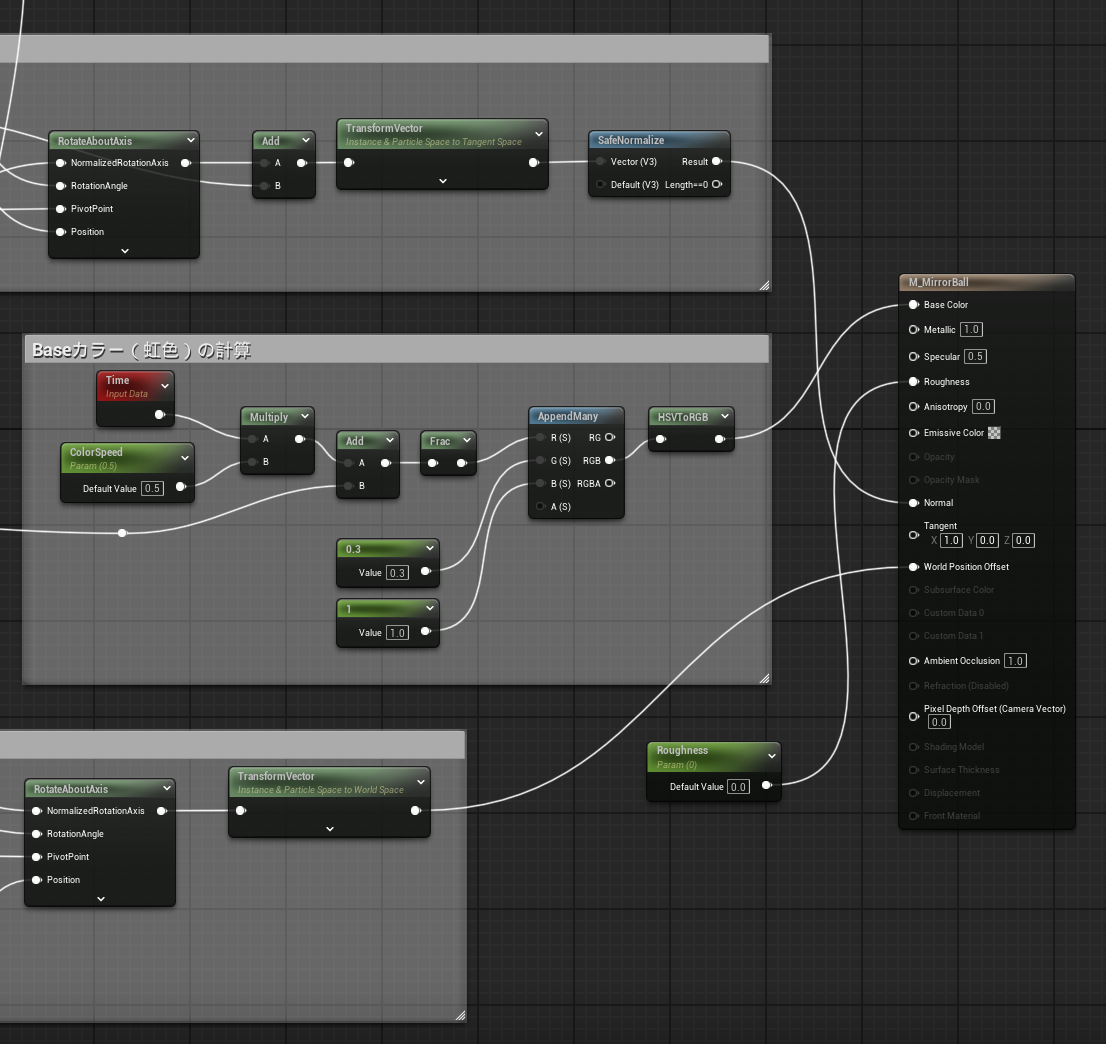
マテリアル全体図と部分拡大図
上記の仕込み情報と操作したいパラメータを絡めて表現したいロジックを組んでいきます。こちらは全体図と部分拡大図を載せておきます。
習作の本質部分ではないけど、ここが一番苦労した…
ファイル配布：Files Distribution
↓のリンクから「MirrorBallAssets_UE5_5_Houdini20_5.zip」をダウンロードしてください。
Download “MirrorBallAssets_UE5_5_Houdini20_5.zip” from the link below.
「UE Content」フォルダにはUEのアセットが入っています。その中にある「MirrorBall」フォルダを、導入したいプロジェクトのContentフォルダ下にコピーしてください。
The “UE Content” folder contains UE assets. Copy the “MirrorBall” folder in it under the Content folder of the project you wish to install.
Discussion