三角関数が流行っているのでPrologで三角述語を書いてみた
一味違う“三角関数”
最近Twitter民が三角関数の実用性について語る風潮がある。その中、違う意味での三角関数についてmattnさんが面白いことを呟いた。
つまり、△を関数名として使えるか? Go・Rust・Javascriptはダメらしい。
しかしPrologはどうだろう?
Prologは関数の代わり[1]に「述語」がある論理プログラミング言語である。
早速“三角述語”を書いてみた。
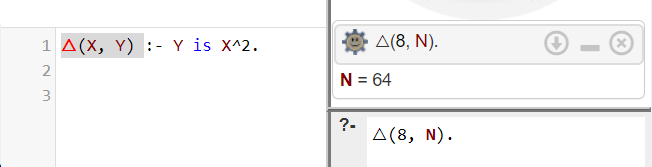
△(X, Y) :- Y is X^2.
YをXの2乗にする適当な述語である。
実行してみる
ネット上でSWI-Prologを実行できるSWISHというplaygroundらしきサイトを使う。
👉 https://swish.swi-prolog.org/p/SZmwYqJP.pl
左側のエディターに上記のプログラムを入れて、右側のテキストボックスに適当なクエリを入れる。例えば、
△(8, N).
を入れてRunを押す。
これは命令型プログラミングで言うと「N = △(8);」みたいなことをしている[1:1]。
結論
Prologで三角関数が書ける!
更なる三角らしさを求めて
△述語は無事に使えたとはいえ、自乗はあまり三角らしくない。むしろ四角いである。反省を踏まえてピタゴラスの定理を実装することにした。これは世界で最も三角らしい物だと言えよう。
clp(fd)を使って制約プログラミングしてみる
clp(fd)とはConstraint Logic Programming over Finite Domainsの略で、有限領域(整数)を扱う制約プログラミングのライブラリである。整数限定なのでピタゴラス数の実装となる。
clp(fd)の詳細ついてM.Hiroi先生の制約論理プログラミング超入門が分かりやすい。
:- use_module(library(clpfd)).
△(C, A, B) :-
C #> 0,
A #> 0,
B #> 0,
C^2 #= A^2 + B^2.
色々なクエリを投げてみる
👉 SWISHで実行できる。
まず、全ての引数に整数を入れて真偽を確かめてみる。
?- △(5, 4, 3).
true
?- △(5, 4, 2).
false
「△(5, 4, 3)は有効な三角であるか?」という意味のクエリ。
変数を1つ投げて検索する
今度は変数を投げてBの値を検索してみる。
?- △(5, 4, B).
B = 5
もちろん他の値も検索可能。
?- △(5, A, 3).
A = 4
変数を2つ投げて検索する
複数の変数を使う場合はlabelに変数を渡して検索できる。
?- △(5, A, B), label([A, B]).
A = 3, B = 4 ;
A = 4, B = 3.
2つの答えが返ってきた。
全てのピタゴラス数を求める
それでは変数を3つ投げてみよう。
?- △(C, A, B), label([C, A, B]).
ERROR: Arguments are not sufficiently instantiated
エラーが返ってきた。変数のどれかに領域を与えないといけないようだ。
?- C in 1..100, △(C, A, B), label([C, A, B]).
C = 5, A = 3, B = 4 ;
C = 5, A = 4, B = 3 ;
C = 10, A = 6, B = 8 ;
C = 10, A = 8, B = 6 ;
...
A #> B を入れて余計な答えを排除。
?- C in 1..100, A #> B, △(C, A, B), label([C, A, B]).
C = 5, A = 4, B = 3 ;
C = 10, A = 8, B = 6 ;
C = 13, A = 12, B = 5 ;
C = 20, A = 16, B = 12 ;
...
labelingで検索方法をいじることも可能。
例えば、順番を逆にしてみる。
?- C in 1..10000, A #> B, △(C, A, B), labeling([down], [C, A, B]).
C = 10000, A = 9600, B = 2800 ;
C = 10000, A = 9360, B = 3520 ;
C = 10000, A = 8432, B = 5376 ;
...
様々な設定がある。実行方法の柔軟性はPrologの強みの1つである。
結論
Prologと制約プログラミングで最強[2]の「△関数」が書ける。
Discussion