Fisher正確検定における両側p値の算出
2×2表の解析において、独立性の検定を行う際に算出するp値についてFisher-p値やカイ2乗分布による近似を用いた算出方法などがある。Fisher-p値では本質的には片側p値を考えるが、状況によっては両側p値の算出の方が好ましい場合もあり、両側p値の算出方法にはいくつか異なる計算方法がある。
本記事では岩崎学先生の書かれた「mid-P value:その考え方と特性」の文献を読んで、Fisher直接検定による両側p値の算出手法の要約とそれら手法の自分なりの吟味を行った。
文献
- 岩崎学. mid-P value: その考え方と特性. 応用統計学. 1993; 22(2): 67-80.
- 丹後俊郎. 医学への統計学 (第3版). 朝倉書店. 2013.
- Cox, D.R. and Snell, E.J.. Analysis of Binary Data, Second Edition. Chapman and Hall, London. 1989.
- 柳川尭. 離散多変量データの解析. 共立出版. 1986.
目次
- Fisher直接検定
- 両側p値の算出
- 考察
1. Fisher直接検定(Fisherのexact test)
以下のような
表1. 数値例
| イベントあり | イベントなし | 計 | |
|---|---|---|---|
| 治療A | 1 | 19 | 20 |
| 治療B | 4 | 6 | 10 |
| 計 | 5 | 25 | 30 |
Fisher直接検定での仮説は、2グループ間でのあるイベントの発現頻度に差があるかどうかであり、
である。
この時に周辺度数を固定した下で、各セルの度数が超幾何分布に従うことを用いて、片側p値を算出する。
治療Aでイベントありの度数(左上のセル)を確率変数
表2. 確率変数表示とした場合
| イベントあり | イベントなし | 計 | |
|---|---|---|---|
| 治療A | 20 | ||
| 治療B | 10 | ||
| 計 | 5 | 25 | 30 |
帰無仮説「
となり、極端なデータは以下のようなイメージ
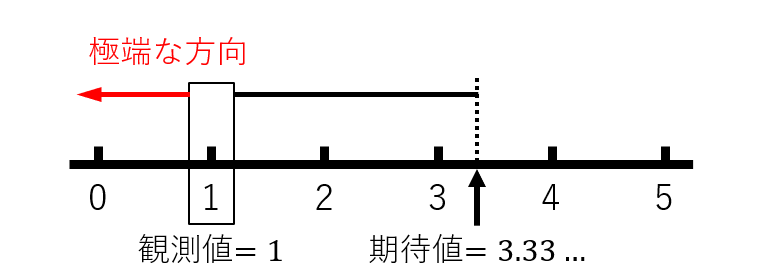
今回では期待値が3.33で、観測値が1なので、期待値から観測値へ向かう方向として捉えればよく、極端なケースは観測状況を含む
片側p値は
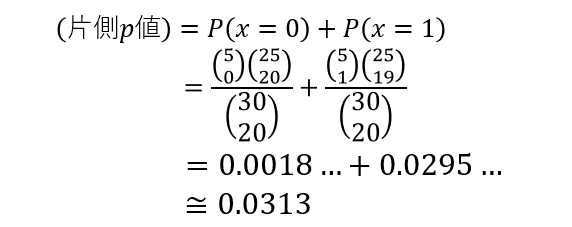
なお、
※ 四捨五入しているので表値を足してもぴったり1にはならない
表3.
| 確率 |
|
|---|---|
| 0 | 0.0018 |
| 1 | 0.0295 |
| 2 | 0.1600 |
| 3 | 0.3600 |
| 4 | 0.3400 |
| 5 | 0.1088 |
2. 両側p値の算出
両側p値の算出には3つの考え方がある。
- 片側p値を2倍にする方法
- 片側p値で考えた度数と反対方向の度数を考え、得られたデータの起きる確率よりも小さな確率で起きるケースの確率を足し合わせる方法
- 得られたデータと帰無仮説の下での期待度数の差による方法
1の片側p値を2倍する方法については、丹後(2013)で推奨しているほか、Cox and Snell(1989)もこの方法を採用している。3の方法は、柳川(1986)で主張されている。
統計ソフト別では、
- SAS freq proc: 方法2
- R fisher.test(): 方法2
- JMP : 方法2
となっており、デフォルトではいずれも方法2の算出方法である
(オプションなどで他の算出方法の指定ができるかも)。
表1での数値例に対して、3つの方法による両側p値を算出してみる。
方法1. 片側p値を2倍
方法2. 片側p値で考えた度数と反対方向の度数を考え、得られたデータの起きる確率よりも小さな確率で起きるケースの確率を足し合わせる方法

片側p値で考えた方向と反対方向というのは、
今回観測されたデータ
そのため、この状況では、両側p値も0.0312と算出される。
方法3. 得られたデータと帰無仮説の下での期待度数の差による方法
まず得られたデータと期待度数の差の絶対値を求める。この差の絶対値は
である。片側p値で考えた方向と反対方向において、期待値と差の絶対値を足した値以上となる度数の確率を片側p値に足し合わせて求める計算となる。すなわち、
となり、
と両側p値が求まる。
3. 考察
数値例から見て取れる通り、必ずしも3種の方法から得られる両側p値は一致するとは限らない。
方法1の片側p値を2倍するという方法は計算が簡便であるが、単純に2倍するという操作は超幾何分布が左右対称、すなわち周辺度数が等しい状況でないと妥当な結果にならないのではないかと考えられる。今回扱った数値例のように各群の人数に偏りがある場合は、この方法1は好ましくないと感じる。
方法3に関しても、期待値を軸として得られたデータとのずれを用いて両側p値を算出しているため、扱うデータの超幾何分布が左右非対称(群間での人数がアンバランス)である場合は、同様に好ましくないのではないかと考えられる。
消去法的な発想であるが、方法2による計算方法が無難であると思う。
とはいっても、計算の流れや考えやすさの点では方法1が一番シンプルなので、群間の人数が偏りなく、ほぼ同じ状況であれば方法1でも問題ないように思う。適用状況に応じて計算方法を選択して、適宜好ましいと考えられる方法を使い分けることが重要であるだろう。
また本記事の本題からは逸れるが、Fisher-p値の他にmid-p値というものもある。
こちらはFisher直接検定を行う際のp値の算出方法で、観測された度数の起きる確率を1/2にして、p値を算出するという方法である。
Fisherの片側p値と比較すると(表1のデータより)、
となる。mid-p値はFisher-p値が第一種の過誤確率を厳密に制御しすぎて(有意水準よりも小さな値となる)、検出力不足を解消しようとしている計算方法らしいが、
丹後(2013)では、mid-p値に関してはいろいろと議論が多く、特別な事情がない限り、通常のFisher-p値を扱うよう、推奨している。
また機会があれば、この辺りもまとめてみたい。
本記事に対して、コメントや感想でも下さると嬉しいです。
もし間違いやおかしな箇所がありましたら、後学のためにも教えてくださると幸いです。
Discussion