Zenn
📖

暗号技術入門を読んだメモ

2022/12/13に公開
Python
#
暗号
tech

暗号技術入門を読んだので、気になったトピックを書きます。
各技術の関連や連携もなかなか面白いです。
イメージしやすいように、自作のpythonコードや画像も掲載しています。

共通鍵暗号

暗号化と復号化で同じ鍵を使う。つまり送信者と受信者であらかじめ同じ鍵を共有しておく必要がある。これは鍵配送問題と呼ばれ、後述する公開鍵暗号などの方法で解決していく。共通鍵暗号のアルゴリズムにも種類があるが、以下気になった二つ「使い捨てパッド」、「AES」について述べる。

使い捨てパッド

メッセージと同じ長さのbit列が鍵となる。メッセージと鍵でXORを取ると暗号化される。XORなので同じ鍵で当然復号化できる。ブルート・フォース・アタック(総当たり攻撃)をされても、攻撃者はどれが正解なのか分からない。なぜなら復号化中に存在するすべてのパターンに出現するためである。よって"暗号化"という意味では最強である。ただし鍵の長さがメッセージの長さと同じなので、単純にデータが二倍になるという問題から、現在ではあまり使われていない。
pythonで書くと下記のような感じになる。

key = [34, 120, 110] # Asciiは7進数なので0~127まで
message = b"cat"
locked_message = [k^m for k,m in zip(key, message)]
unlocked_message = [k^u for k,u in zip(key, locked_message)]
print("".join(map(chr,message))) #cat
print("".join(map(chr,locked_message))) #key次第の意味が分からない3文字
print("".join(map(chr,unlocked_message))) #cat

AES

現在最も多く使われている対象暗号はAES(Advanced Encryption Standard)である。AESという名を基に2000年に優秀な対称暗号アルゴリズムコンペが行われ、Rijindaer(ラインダール)というアルゴリズムが選ばれた。
他にも対称暗号のアルゴリズムとして、DESやトリプルDESなどがあるが、現在では非推奨だったりする。

公開鍵暗号

共通鍵暗号では鍵配送問題が発生する。そこで公開鍵暗号が発明された。受信者は「公開鍵」と「秘密鍵」を作成し、送信者は「公開鍵」でメッセージを暗号化する。受信者は「秘密鍵」でメッセージを復号化する。「公開鍵」は誰に知られても問題ないが、「秘密鍵」は受信者以外には知られないようにする。
なお公開鍵暗号では、「受け取った公開鍵は本当に受信者のものか？」という問題が残る。これは後述するデジタル署名や証明書などの組み合わせで解決する。

RSA

現在最も主流な公開鍵暗号である。平文m、暗号文cとすると、以下の数式で暗号化、復号化を行う。ここで(E,N)のペアが公開鍵、(D,N)のペアが秘密鍵となる。受信者はあらかじめ決められた計算で(E, D, N)を算出する。計算方法は調べればたくさん出てくるため省略。

  • 暗号化：　 c = m^E modN
  • 復号化：　 m = c^D modN

pythonで書くと下記のようになる。

E,D,N=5,29,323
def rsa_encrypt(i):
    return (i**E)%N
def rsa_decrypt(i):
    return (i**D)%N
message = b"cat"
locked = list(map(rsa_encrypt, message))
unlocked = list(map(rsa_decrypt, locked))
print("".join(map(chr, message))) #cat
print("".join(map(chr, locked))) #key次第の意味が分からない3文字
print("".join(map(chr, unlocked))) #cat

Diffie-Helman鍵交換

公開鍵暗号ではないが、盗聴されずに鍵を共有する方法の一つ。なんと誰にでも知られてよい数から、「送信者」と「受信者」だけが作れる数(鍵)を作成できる。

  1. 素数Pとその生成元Gを用意する
  2. 1~P-2の間で通信者はそれぞれ乱数A,Bを用意する。
  3. 通信者はそれぞれG^A mod PとG^B mod Pという値を計算し交換する。
  4. それぞれ(G^A mod P)^B mod Pと(G^B mod P)^A mod Pを計算する
  5. どちらもG^{A×B} mod Pという値が生成される。

これはG^A mod Pから数Aを計算することが難しいことから成り立つ。(離散対数問題という)

ハイブリッド暗号システム

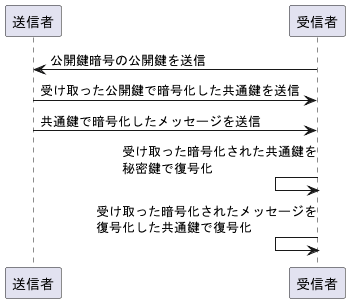
公開鍵暗号は処理が遅いのでそれだけで暗号化するとパフォーマンスが良くない。一方、共通鍵暗号は比較的処理が速い。そこで送信者は、メッセージを共通鍵暗号の鍵で暗号化し、その鍵を受信者の公開鍵暗号の公開鍵で暗号化する。その後、受信者は自身の秘密鍵で共通鍵を復号化し、その復号化した鍵でメッセージを復号化する。

ハイブリッド暗号システムの流れ

一方向ハッシュ関数

任意の長さの入力を固定長の出力に変換する。人間で言う指紋みたいなもの。出力はハッシュ値、フィンガープリントなどと呼ばれる。例えば二つのファイルが同一か検証したい場合ファイル自体を比較するのではなくそれぞれのハッシュ値を比較することで、素早くファイルの改竄を検出することができる。なお名前の通り、ハッシュ値から入力を逆算することはできない。
また一方向ハッシュ関数では改竄は検知できるが、なりすましは検知できないので、後述するメッセージ認証コードやデジタル署名を利用して、認証する必要がある。

弱衝突耐性,強衝突耐性

ハッシュ関数は固定長のbit列を出力する。つまり理論上はハッシュ値がかぶる場合がある。これを衝突と呼ぶ。当然ハッシュ値が衝突しづらい設計となるべきである。

  • 弱衝突耐性
    あるメッセージとハッシュ値があるとき、そのハッシュ値になるような同じメッセージを見つけることに対する耐性
  • 強衝突耐性
    同じハッシュ値を持つ任意の二つのメッセージを見つけることに対する耐性

有名な一方向ハッシュ関数

MD4,MD5,SHA-1,SHA-2,SHA-3,RIPEMD-160などがある。MD系、SHA1は衝突耐性が破られているので新規で使うべきではない。SHA-2はまだまだ現役だが、SHA-1が非推奨になった時点でSHA-3(KECCAC)が次世代の一方向ハッシュ関数として選ばれた。ちなみにRIPEMD-160はビットコインで使われている。
下記はpythonでSHA-256を利用した例である。入力が一文字変わるだけで出力が全く変わること、任意の長さの入力が固定長の出力になっていることが分かる。SHA-256の出力は256bitだが出力は16進数なので32桁になっている。

import hashlib
m = hashlib.sha256()
l = [b'a', b'b', b'ccccc']
for i in l:
    m.update(i)
    print(m.hexdigest())
#ca978112ca1bbdcafac231b39a23dc4da786eff8147c4e72b9807785afee48bb
#fb8e20fc2e4c3f248c60c39bd652f3c1347298bb977b8b4d5903b85055620603
#32d050c3fae773053e288c5cd50350b1dca295445532079893c854ba898911c1

メッセージ認証コード

Message Authendication Code を略してMACと呼ばれることが多い。鍵に依存した一方向ハッシュ関数である。出力はMAC値などと呼ばれる。つまり鍵を知っている人しか作成できない値を作り出すことができる。代表的なアルゴリズムとしてはHMACなどがある。メッセージ認証コードもあらかじめ鍵の共有が必要になることから、後述するデジタル署名などを用いて、解決する必要がある。IPsecやSSL/TSLで使用される。
メッセージ認証コードでなりすましは検出できるが、第三者への証明や否認防止ができない。

メッセージ認証コードへの攻撃

有名なものとして再生攻撃と呼ばれるものがある。攻撃者はMAC値は計算できないが、MAC値を盗聴してその後もそれを送り続ける。MAC値を計算する際にシーケンス番号や時刻情報、ノンス(ランダムな値)など、そのときを一意に指定できる値使うことが対策として考えられる。

デジタル署名

メッセージのハッシュ値をプライベート鍵で暗号化することを署名するという。この値はプライベート鍵を持っている人にしか作り出せない。この署名の確認を行うことを検証するという。検証は公開鍵を持つ者ならだれでも可能であり、署名された値を公開鍵で復号化し、メッセージのハッシュ値と比較して一致していれば、検証に成功したと言える。デジタル署名はちょうど公開鍵暗号の逆を行うイメージである。
なお検証に使用する公開鍵が本物かどうかを判断することが必要で、後述する証明書を利用する必要がある。

デジタル署名の流れ

証明書

公開鍵を登録したいユーザーは認証局に渡し、認証局がその鍵に対して自身の秘密鍵でデジタル署名を施す。公開鍵を利用したいユーザーは認証局の公開鍵で検証を行い、検証を行った結果が妥当ならば正しい公開鍵を得ることができる。
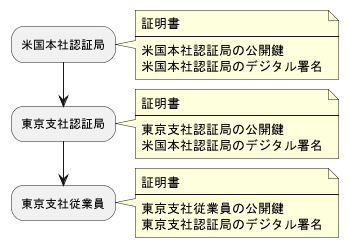
認証局の公開鍵は正しいのか？という疑問が残るが、多くの場合認証局は再帰的な親子関係になっており、親の認証局が子の認証局の公開鍵に対してデジタル署名を連鎖的に行う。ルート認証局(これ以上親がいない認証局)が自身の公開鍵を自身の秘密鍵でデジタル署名を行っている。有名な認証局の公開鍵はデフォルトでPCに入っている場合などもあり、ユーザーは知らないうちに認証局を認証した結果、他の認証局の公開鍵も妥当だと判断できるのである。
下記の図は認証の流れを図にしたものである。従業員はルートCAである米国本社認証局の公開鍵を既に持っているという前提から、米国本社認証局の公開鍵→東京支社認証局の公開鍵→東京支社従業員の公開鍵を順に検証しながら取得する。

認証の流れ

証明書関連の用語

  • PKI
    Public-key Infrastructureの略で証明書関連全般のルールのこと
  • CA
    Certification Authorityの略で日本語だと認証局
  • CRF
    Certificate Revocation Listの略で、証明書の破棄リストである。使用しなくなった証明書のシリアル番号の一覧に対して、認証局がデジタル署名している。

乱数

暗号技術の中で、乱数は多くのケースで使用される。乱数の種類には以下が存在する。

  • 無作為性
    一見無作為に抽出された値に見えるが、過去に抽出された値の数列を見れば次が予測できる可能性がある乱数。ゲームやシミュレーションではこれで良いケースも多い。
  • 予測不可能性
    過去に抽出された値の数列を見ても、次の値が予測できない乱数。暗号技術で使用する乱数の必要条件である。
  • 再現不可能性
    ソフトウェアは何かしらの内部状態を持つので、この乱数を抽出するのは不可能である。よってハードウェアの力を借りることになる。これが真の乱数であるため、上記二つの生成器は疑似乱数生成器と呼ばれることが多い。

線形合同法

Cのライブラリ関数であるrandやJavaのjava.util.Randomで使用されているのがこれ。予測不可能性はないので暗号アルゴリズムなどで使うべきではない。pythonで書くと下記のような形になる。

#A,Cは0以上M未満にする
M,A,C,seed=14,12,11,5
while True:
    r = (A*seed+C) % M
    seed = r
    print(r)

1方向ハッシュ関数を使う方法

シードを初期の内部状態として、そのハッシュ値を初回の乱数とする。次に内部状態に+1を行いそのハッシュ値を次の乱数とする。これを繰り返すことで予測不可能性を持った疑似乱数生成器を作成できる。一方向ハッシュ関数によって内部状態を予測することは難しい。
ふと思ったのだが、この方法でハッシュ値より長い回数計算したらハッシュ値が衝突すると思ったが、出力ハッシュ値のbit数が256とかだと現実的には難しそう。そもそもそれによって出力が周期的になるわけではないからそんなに問題はなさそう。pythonで書くと下記のような形になる。

import hashlib
m = hashlib.sha256()
seed = 0
while True:
    m.update(bin(seed).encode())
    seed+=1
    print(m.hexdigest())

SSH/TSL

現在のセキュアな通信技術を支える、最も使われている技術という認識。HTTPだけではなく、メール系のSMTPやPOP3の下の層にも乗る。SSH/TSLはフレームワークであり、実際にどの暗号技術を使うかは使用するブラウザやサーバーのソフトウェアにより変わる。
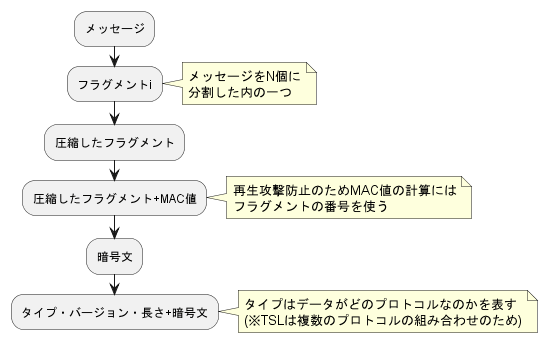
決められたプロトコルに従って通信の開始時に使用する暗号アルゴリズムや共通鍵の共有などを行った後、以下の画像の流れでメッセージを暗号化する。事前の共有部分はTSLの中でもハンドシェイクプロトコルと呼ばれるが、ここは結構複雑。

SSH/TSlの暗号化

参考

暗号技術入門

GitHubで編集を提案

Discussion