数理最適化で看護師のシフト(勤務表)を自動生成してみた
最近、看護師のシフト(勤務表)の自動生成について調査したので、その内容を少しご紹介しようと思います。
Colab で実装したので、リンク貼っておきます。
シフト作成って思っているより難しい
シフトの作成は職員のシフト希望やスキル、労務規定など考慮しないといけないことが多く、実はかなり複雑です。
看護師のシフト(勤務表)作成をピックしたナーススケジューリング問題というテーマが存在するぐらいです。
参考
"pulp"と"deap"はシフトの救世主かもしれない
シフト作成のについて調査すると、Python のpulpとdeapというライブラリのどちらかで解く記事によくヒットします。
整理すると、、、
-
pulpは数理最適化を行うためのライブラリで、シンプルな(線形な)制約を考慮したシフト作成に向いている。 -
deapは遺伝的アルゴリズムを利用するためのライブラリで、複雑な(非線形な)制約を考慮したシフト作成に向いている。
遺伝的アルゴリズムは、生物の進化の過程で起きる「環境に適応し、より強い個体が生き残り、環境に適応できない弱い個体は淘汰される」という現象を再現したアルゴリズムならしいです。
"pulp"でモデルを作ってみた
今回は試しなので、簡易な条件を pulp で解いてみます。
- 看護師さんが毎月、1 ヶ月分のシフト希望(休みの希望)を提出する。
- 勤務形態として"早番"と"遅番"が存在する。
- "早番"と"遅番"が連続しないようにシフトは組まれる。
- 日単位の必要な看護師の人数が決まっている。
- 新人の看護師さんができる限り被らないようにする。
本来は、主任が必ず一人いる状態にする、シフトだけでなく配置先も考慮する、などもっと制約は複雑になると思います。
条件の整理
まずはじめに条件をベースに、制約条件と最適化する目的を定義します。
制約条件は基本的に守らないといけないもので、最適化する目的はできる限り守りたいものです。
いわゆる "よしなに" を実現するのが部分が最適化する目的です。
制約条件
- 職員のシフト希望(休みの希望)。
- 日単位の必要な看護師の人数。
- 今回は 1 日に"早番"が 2 人、"遅番"が 2 人必要ということにします。
最適化する目的
- "早番"と"遅番"が連続しない。
- 新人の看護師さんができる限り被らない。
テストデータの作成
1 ヶ月を 30 日として、看護師さんのシフト希望(休みの希望)を休み希望を 1、それ以外を 0 のリストで表現することにします。
class Nurse:
def __init__(self, name, is_newcomer):
self.name = name
self.is_newcomer = is_newcomer
self.shift_request = shift_request
def set_shift_request(self, shift):
self.shift_request = shift
def set_shift(self, shift):
self.shift = shift
shift_request = [
0,0,0,0,0,0,0,
0,0,0,0,1,1,0,
0,0,0,0,0,0,0,
0,0,0,0,0,0,0,
0,0
]
tanaka_tarou = Nurse('Tanaka Tarou', False)
tanaka_tarou.set_shift_request(shift_request)
"pulp"でモデリング(制約条件)
pulpで下記の制約条件をモデル化します。
- 職員のシフト希望(休みの希望)。
- 日単位の必要な看護師の人数。
- 今回は 1 日に"早番"が 2 人、"遅番"が 2 人必要ということにします。
import pulp
import random
# 日単位の必要な看護師の人数
request_nurses_per_early_shift = 2
request_nurses_per_late_shift = 2
# 勤務形態(早番: e, 遅番: l, なし: -)
shift_types = ['e', 'l', '-']
# モデルの定義
lp_model = pulp.LpProblem("ShiftScheduling", pulp.LpMinimize)
x = pulp.LpVariable.dicts("shift", (range(len(nurses)), range(n_days), shift_types), cat="Binary")
# 目的関数
# 後で、実装...
for d in range(n_days - 1):
# 日単位の必要な看護師の人数の制約
lp_model += pulp.lpSum(x[n][d]['e'] for n in range(len(nurses))) >= request_nurses_per_early_shift
lp_model += pulp.lpSum(x[n][d]['l'] for n in range(len(nurses))) >= request_nurses_per_late_shift
for n in range(len(nurses)):
# 職員のシフト希望(休みの希望)の制約
if nurses[n].holiday_request[d] == 1:
lp_model += x[n][d]['-'] == 1
lp_model.solve()
結果
良い感じの結果が出ました。
※(x)はシフト希望(休みの希望)にそぐわないシフトです。
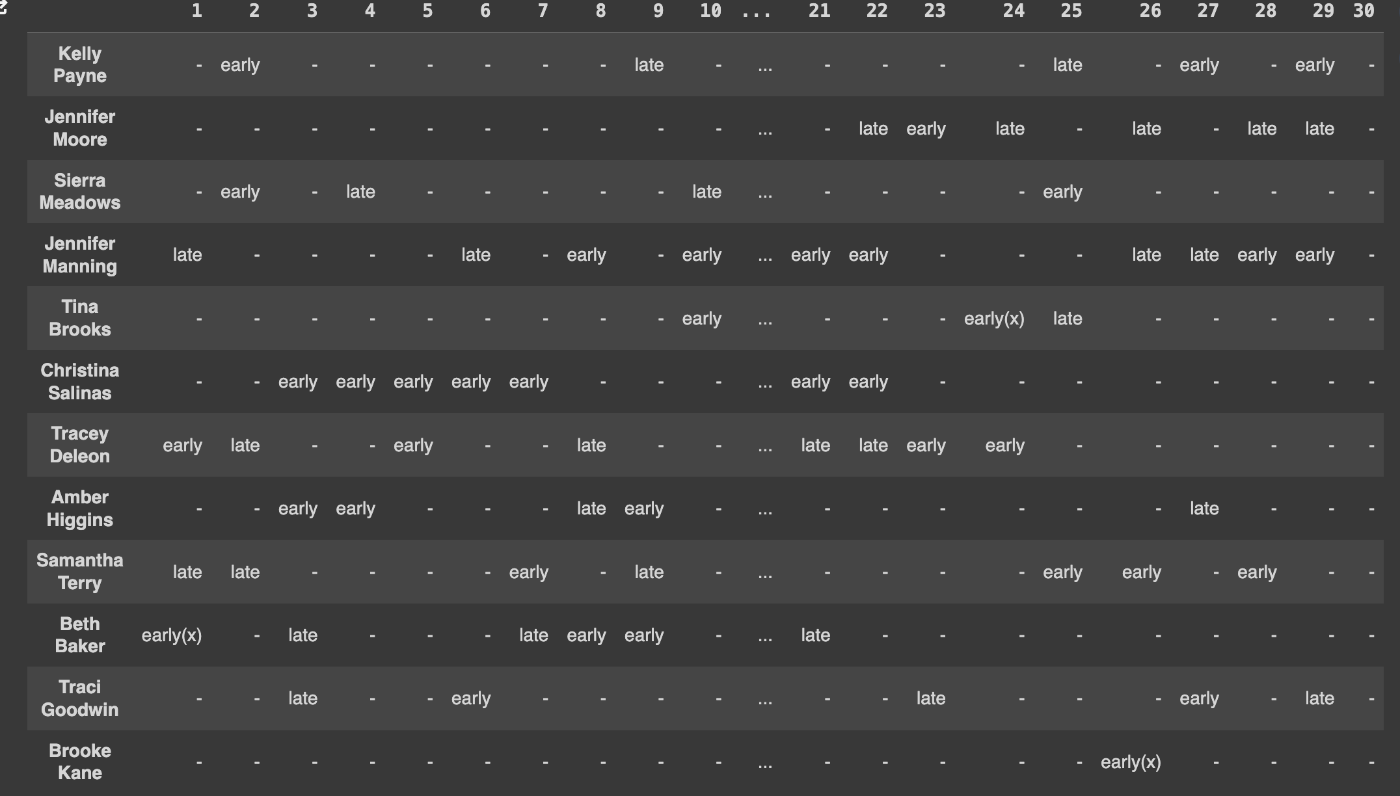
制約条件をモデル化できたので、次は最適化する目的をモデル化します。
"pulp"でモデリング(最適化する目的)
pulpで下記の最適化する目的をモデル化します。
- "早番"と"遅番"が連続しない。
- 新人の看護師さんができる限り被らない。
各条件にペナルティー値を設定し、その合計値を最小化するように実装します。
この実装を目的関数と呼ぶらしいです。
"早番"と"遅番"が連続しない。
目的関数は(今日は早番で次の日は遅番を禁止するみたいな)非線形な条件を直接組み込むことはできません。
そのため、補助変数 y を導入し間接的に条件を組み込み込んでいます。
# 補助関数
y = pulp.LpVariable.dicts("consecutive_shift", (range(len(nurses)), range(n_days-1)), cat="Binary")
# 連続シフトのペナルティー値
penalty_consecutive_shift = 10
for n in range(len(nurses)):
for d in range(n_days - 1):
lp_model += y[n][d] >= x[n][d]['l'] + x[n][d+1]['e'] - 1
lp_model += y[n][d] >= x[n][d]['e'] + x[n][d+1]['l'] - 1
# 連続シフトの目的関数
lp_model += pulp.lpSum([y[n][d] for n in range(len(nurses)) for d in range(n_days - 1)]) * penalty_consecutive_shift
新人の看護師さんができる限り被らない。
目的関数で実現するのが難しそうなので諦めました...
制約条件としてなら、下記のようにすることで実装可能です。
for d in range(n_days - 1):
# 日単位の必要な看護師の人数の制約
# ...
for n in range(len(nurses)):
# 職員のシフト希望(休みの希望)の制約
# ...
# 新人の看護師さんが被らない制約
for s in shift_types:
newcomer_assignments = pulp.lpSum(x[n][d][s] for n in range(len(nurses)) if nurses[n].is_newcomer)
lp_model += newcomer_assignments <= 1
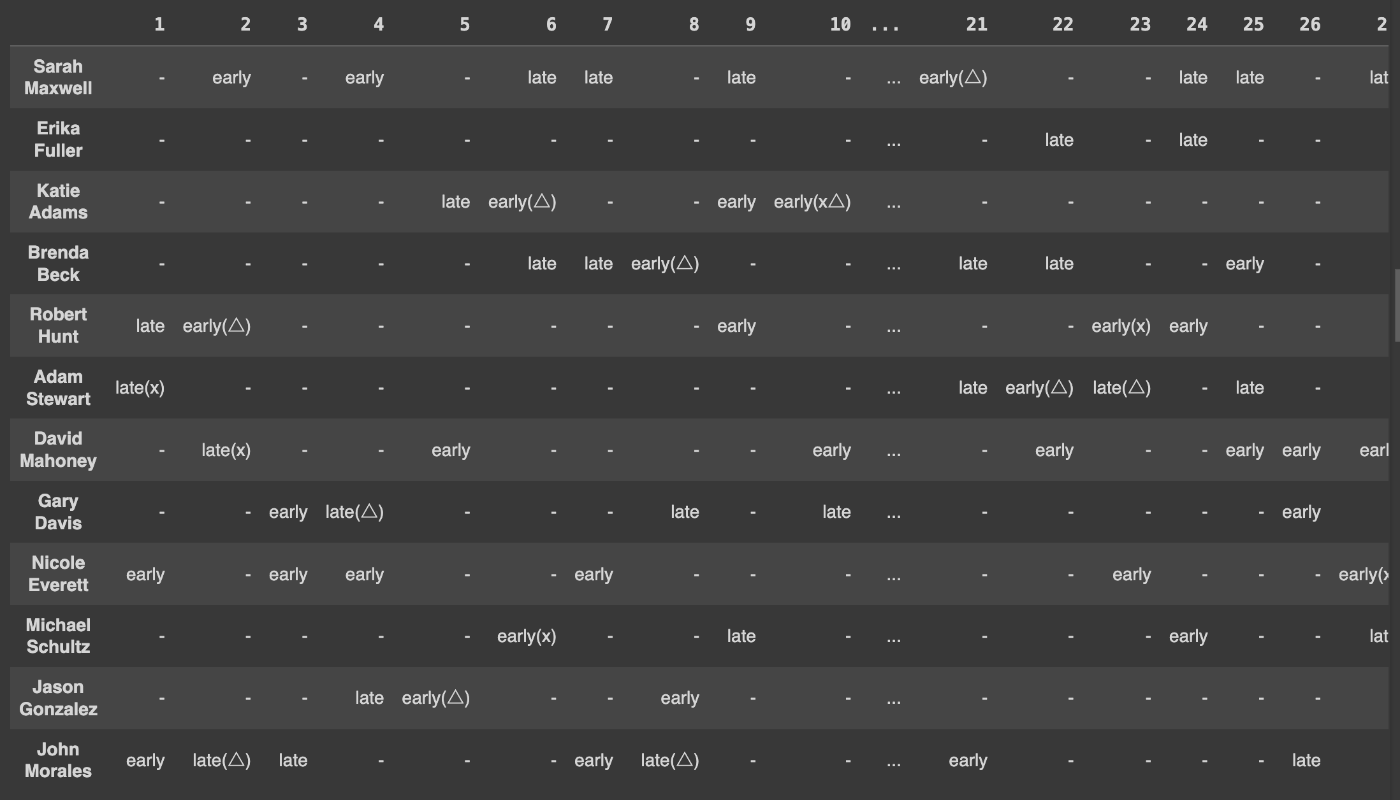
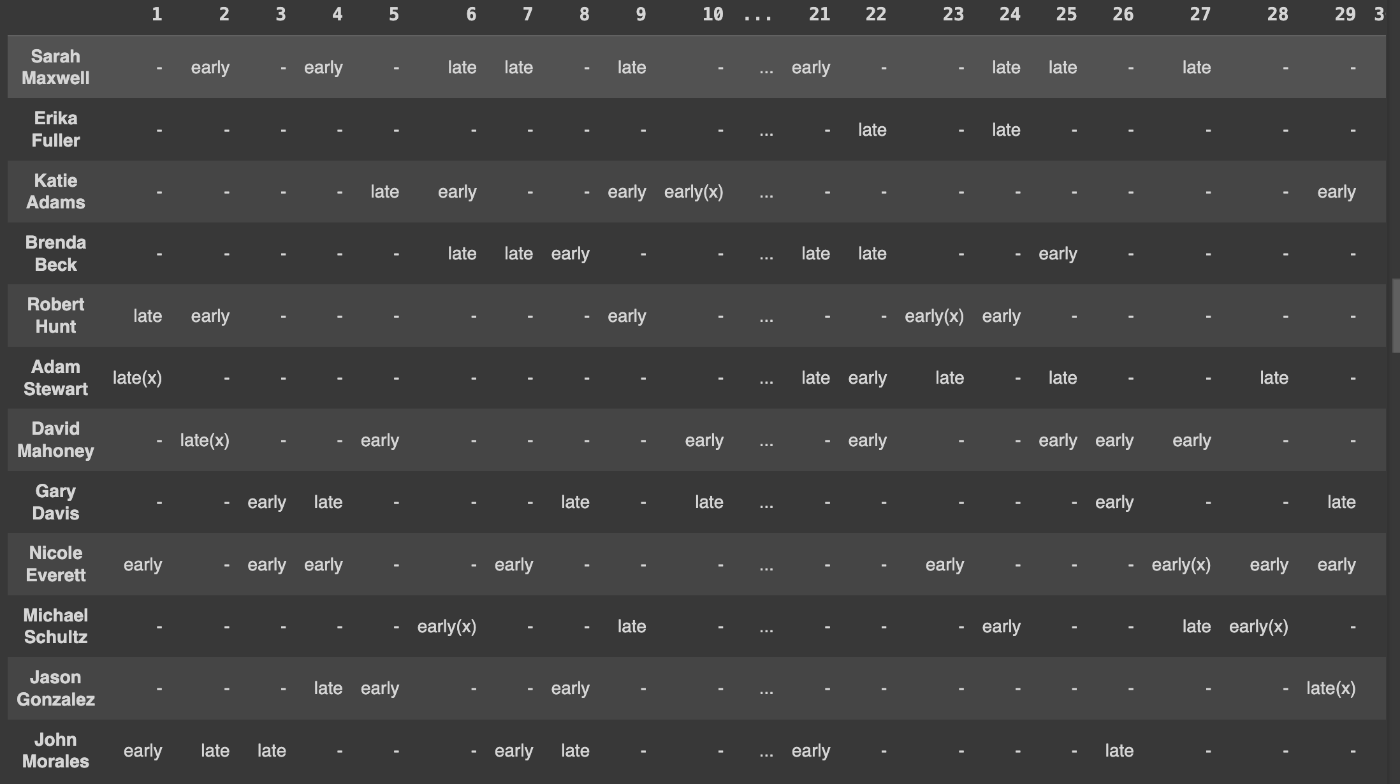
結果
目的関数も期待通り機能していそうです。
※(△)はペナルティー対象のシフトです。
実装前
実装後
感想
アルゴリズムを使えば、案外精度高くシフトを自動生成できそう。
ただ、"pulp"は目的関数周りの制約が厳しいため、実装する前に確認しておいた方がよさそう。
※"deap"も気が向けば、記事書こうと思います。
Discussion