😺

MySQLのB+ツリーインデックスの概要

2023/09/18に公開

MySQL

インデックスとは

データベースのインデックスは特定のデータを検索するために使用する本の索引のような データ構造です。
インデックスはテーブルのデータとは別の場所に追加の領域を確保して作成される冗長なデータです。インデックスを作成することにより元のデータが変更されることはありません。
インデックスにはテーブルのデータに対する参照が作成され、これを使用してデータの取得を高速化することができます。

インデックスによる高速化について

インデックスが存在しない場合、MySQLは特定の値を見つけるためにテーブル全体を読み取る必要があります。テーブルが小さければ問題ありませんが、大きくなると処理が非常に重くなってしまいます。

インデックスを使用するとデータの取得を高速化できます。インデックスはB+ツリーというデータ構造に格納されています。このデータ構造は二分探索木をベースとしています。

二分探索木とは

二分探索しやすいように値を大小で振り分けたデータ構造です。下図のように親の左側の子ノードに親より小さい値が、右側のノードに親より大きいノードが格納されます。

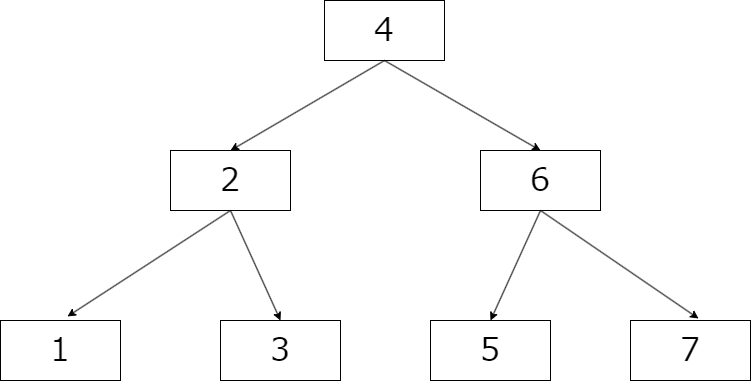
AVL木のような平行二分木の場合は、二分探索によりデータサイズをNとしたときにO( $\log N$ )の計算量で探索できます。
単純なリストで前から順に値を検索するとO(N)の計算量となるため二分探索木により検索が高速化されていることが理解できます。

B+ツリー

B+ツリーの構造

B+ツリーは二分探索木をベースとしていて、1つのノードが最大m個 (m>=2) の子ノードを持つことができる平衡木構造のことです。
最上層のノードをrootノード、最下層のノードをリーフノードと呼び、それ以外のノードをブランチノードと呼びます。
それぞれのノードにはm個以下のエントリが含まれ、各エントリの左側の子ノードにそのエントリの値よりも小さい値が格納され、右側の子ノードにはエントリの値以上の値が格納されます。
末端のリーフノードはポインタで接続されます。
以下は $m=2$ のB+ツリーの例です。

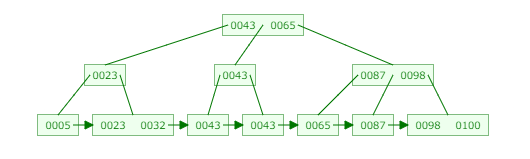
B＋ツリーの検索

上に示したB+ツリーで32という値を検索することを考えてみましょう。
まずrootノードから探索を開始します。ノードの各エントリが検索したい値（32）以上であるかを確認します。
エントリの値が検索したい値（32）以上であれば、そのエントリの左側のエッジをたどります。そうでなければ、次のエントリでも同様に検索したい値（32）以上であれば左側のエッジをたどります。最後のエントリでも検索したい値以上にならなければそのエントリの右側のエッジをたどります。
最初のエントリである43は検索したい値（32）よりも大きいため、43のエントリの左側のエッジをたどります。

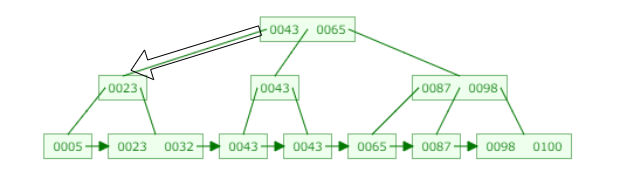
同様に次のノードでも各エントリが検索したい値（32）以上であるかを確認します。最初のエントリの23は32よりも小さいですが、このノードにはエントリが１つしかないので、これが最後のエントリになります。そのため、23のエントリの右側のエッジをたどります。

リーフノードに到達しました。エントリで検索したい値(32)に一致するものを探します。無事に見つかったので検索終了です。

まとめ

MySQLのB+ツリーインデックスのデータ構造について解説しました。B+ツリーは二分探索木をベースとしており、対数時間でデータの検索が可能です。
B+ツリーの構造を理解することはインデックスの最適化に重要です。