【Java】二次元累積和

二次元累積和

二次元累積和とは、二次元配列の矩形領域内の和です。

二次元累積和の図解

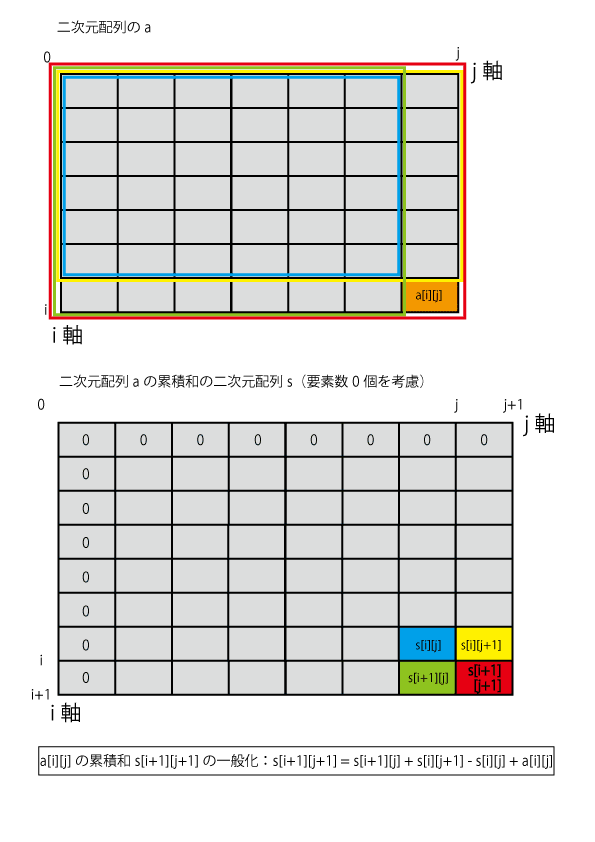
二次元累積和の一般化

• 上記により、二次元配列aの累積和の二次元配列sの一般化は、下記の通りとなります。

  s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + a[i][j]
  

  • 具体例として、二次元配列aを下記の通りとします。

    a = [
        [1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]
        ]
    

  • 要素数0個を考慮する累積和の二次元配列sは、下記の通りとなります。

    s = [
        [0, 0, 0, 0],
        [0, 1, 3, 6],
        [0, 5, 12, 21],
        [0, 12, 27, 45]
        ]
    

  • s[3][3]は45ですが、一般化の式に当てはめてみたいと思います。この時、i=2でj=2となります。

    s[2 + 1][2 + 1] = s[2 + 1][2] + s[2][2 + 1] - s[2][2] + a[2][2]
    s[3][3] = s[3][2] + s[2][3] -s[2][2] + a[2][2]
    45 = 21 + 27 - 12 + 9
    45 = 45
    

    結果が同じになることが分かりました。

---

二次元累積和の区間の和の図解

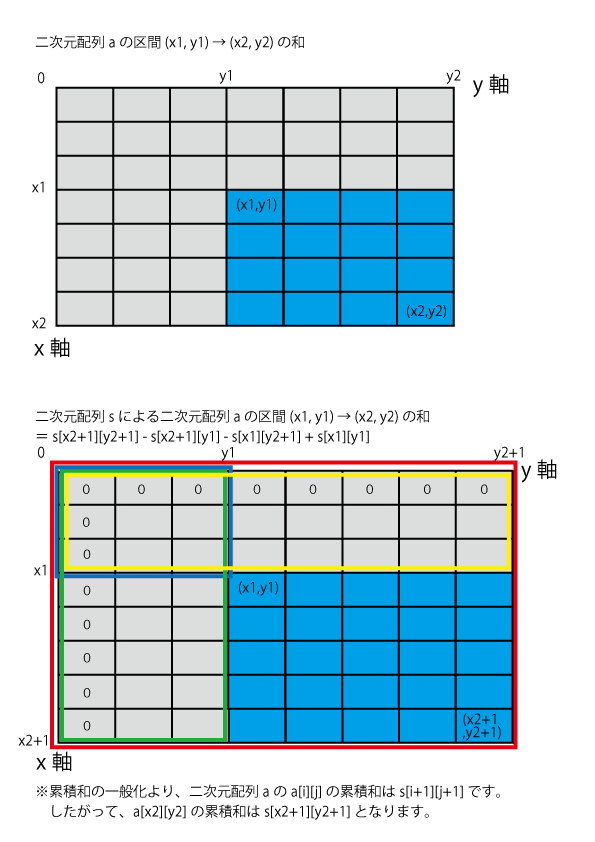
二次元累積和の区間の和の一般化

• 上記により、二次元配列aの区間(x1, y1)→(x2, y2)の和を二次元配列sを使って一般化すると、下記の通りとなります。

  s[x2 + 1][y2 + 1] - s[x2 + 1][y1] - s[x1][y2 + 1] + s[x1][y1]
  

  • 具体例として、二次元配列aを下記の通りとします。

    a = [
        [1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]
        ]
    

  • 要素数0個を考慮する累積和の二次元配列sは、下記の通りとなります。

    s = [
        [0, 0, 0, 0],
        [0, 1, 3, 6],
        [0, 5, 12, 21],
        [0, 12, 27, 45]
        ]
    

  • 区間(x1=1, y1=1)→(x2=2, y2=2)の和は、二次元配列aで言うと5 + 6 + 8 + 9 = 28です。結果が同じになるか、一般化の式に当てはめてみたいと思います。

    28 = s[2 + 1][2 + 1] - s[2 + 1][1] - s[1][2 + 1] + s[1][1]
    28 = s[3][3] - s[3][1] -s[1][3] + s[1][1]
    28 = 45 - 6 - 12 + 1
    28 = 28
    

    結果が同じになることが分かりました。

コード例

コード例の解説はありません。

import java.util.*;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n, m, x1, y1, x2, y2;
        n = sc.nextInt();
        m = sc.nextInt();
        x1 = sc.nextInt();
        y1 = sc.nextInt();
        x2 = sc.nextInt();
        y2 = sc.nextInt();
        int[][] a = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                a[i][j] = sc.nextInt();
            }
        }

        // 累積和の二次元配列 s を作成
        int [][] s = new int[n + 1][m + 1];
        // i が 0 から n-1までのループを回す
        for (int i = 0; i < n; i++) {
            // j が 0 から m-1 までのループを回す
            for (int j = 0; j < m; j++) {
                // 二次元累積和の一般化より、s[i+1][j+1] = s[i+1][j] + s[i][j+1] - s[i][j] + a[i][j]
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + a[i][j];
            }
        }
        // 二次元累積和の区間の和の一般化より、s[x2+1][y2+1]-s[x2+1][y1]-s[x1][y2+1]+s[x1][y1] を出力
        System.out.println(s[x2 + 1][y2 + 1] - s[x2 + 1][y1] - s[x1][y2 + 1] + s[x1][y1]);
    }
}

入力値は下記の通り。

n = 3
m = 3
x1 = 1
y1 = 1
x2 = 2
y2 = 2
a = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

出力結果は下記の通り。

28