Zenn
🗻

地震計の傾斜応答についてのメモ

に公開
地震
火山
地震計
tech

地震計 (特に広帯域地震計) の傾斜応答について考える必要が生じた。資料の行間を埋めるためにわからないなりに考えたことをまとめて置いておく。

以下では電磁式地震計を念頭に置いた簡易的なモデルを考えたが、実用上問題になりそうな広帯域地震計は広帯域での観測を実現するためにフィードバック回路等を使ったより高次の系になる模様。とはいえ、肝心な部分の特性は直感的なイメージ通りになるよう設計されているようだし、参照した資料でも大抵その辺りをうまく誤魔化した説明をしているようであった。イメージはイメージとして持った上で、解析は与えられた極と零点をよく見ながらやれば問題ないだろうと思っている。

地震計のモデル:バネ-質量-ダンパ系の運動方程式

質量を単位量(質量で規格化)、ダンパによる減衰定数をh、バネの固有角周波数を\omega_{0}、入力変位をx_{in}、出力変位をx_{out}とすると、系の運動方程式は以下のように表現できる。

\begin{equation} \ddot x_{out} + 2\omega_0 h \dot x_{out} + {\omega_0}^2 x_{out} = \ddot x_{in} \end{equation}

速度変化に対する伝達関数

ここでは速度変化を単位インパルスで与えたときの系の速度応答をまず確認したい[1]。\dot x_{in}=\delta(t)を(1)式に代入、ラプラス変換。これを速度変化に対する系の伝達関数V_v(\omega) \equiv \mathcal{L}(\dot x_{out})について整理する。

\begin{equation} V_v(\omega)=\frac{s^2}{s^2+2\omega_0hs+{\omega_0}^2} \end{equation}

傾斜変動に対する伝達関数（水平の場合)

傾斜変化を単位ステップで与えたときの系の水平方向の速度応答が見たい[2]。ここで青山 (2008) に倣い、\ddot x_{in}=g\psi H(t) (g:重力加速度; H(t):階段関数) [3]を(1)式に代入して一階微分した上でラプラス変換 (\dot H(t)=\delta (t))。これを傾斜変動に対する系の伝達関数V_{T}(\omega) \equiv \mathcal{L}(\dot x_{out})について整理する (ただし (3)式では\psi=1 radで正規化)。

\begin{equation} V_{T}(\omega)=\frac{g}{s^2+2\omega_0hs+{\omega_0}^2} \end{equation}

速度 vs 傾斜

(2)式と(3)式を比較すると以下のように書ける。

\begin{equation} V_{T}(\omega)=\frac{g}{s^2}V_{v}(\omega) \end{equation}

つまり傾斜変動に対する応答は(水平方向の)速度変化に対する応答を二階積分してgをかけたものになる。

系の極と零点

地震計の特性は極と零点の表でユーザに提供されることが多い。n個の極、m個の零点を持つ地震計の伝達関数は以下のように表現される (ただしAは振幅を補正するための係数)。

\begin{equation} F(\omega)=A\frac{\prod_{j=1}^{m}{(s-z_j)}}{\prod_{i=1}^{n}{(s-p_i)}} \end{equation}

ここで(2)式を見ると、分母が2次、分子も2次の多項式になっている。そのため、例えば今回考えた速度変化に対する系の速度応答を表現する伝達関数は2つの極と2つの零点 (z_{1,2}=0の重解) を持つことがわかる。そこで定常的な震動のみ考え (つまりs=i\omegaとして)、二つの極をp_1、p_2と置いて(2)式と(5)式を連立させて解くと以下の関係が現れる。

\begin{align} p_1+p_2&=-2\omega_0 h \\ p_1 p_2&={\omega_0}^2 \\ \end{align}

ここから、h \ge 1 のときp_{1,2}は実数解 (減衰)、0<h<1のときにp_{1,2}は実数部が負の複素共役解をとり (振動+減衰) 、h=0のときは\pm i\omega_0 (自由振動) となることがわかる。ここでは0\le h \le 1の場合について複素平面上を使いよく確認しておきたい。

複素平面上での各パラメータ

図で表現すると以下のように描ける。(5)式よりRe(p_{1,2})=-h\omega_{0}であることから、0<h<1の条件下では振動しながら指数関数的に振幅が減衰するような応答を示す。そして減衰定数hは複素平面上で虚数軸からの距離、つまり減衰と振動のバランスを決めるパラメータとして図示できる。例えばh=0のときは減衰せず自由振動するし、h=1のときは振動せず減衰する。0<h<1ではその中間的な応答を示す。

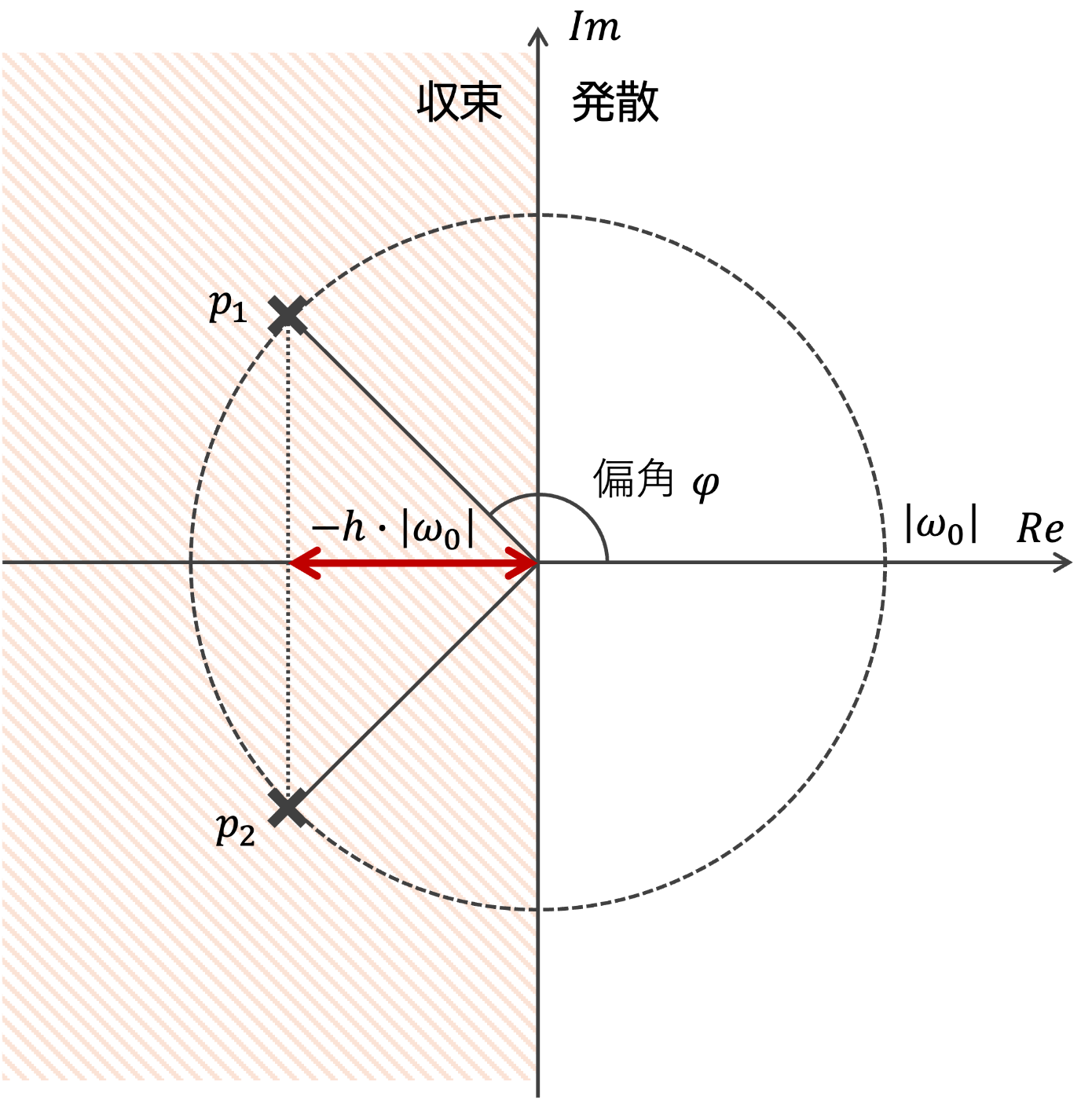
そして、\phi=3\pi/4とすると、系に固有周期付近での共振ピークを抑えるために必要な最小限の減衰がかけられる。これを最大平坦特性を持つ伝達関数と言う。このときh=1/\sqrt{2}=0.707。広くフラットな特性を得ることができるため、このパラメータは一般に電磁式地震計で好んで利用される。h=1/\sqrt{2}=0.707のとき、伝達関数は\omega_0をコーナー周波数とする二次バタワース型ハイパスフィルタと同じ形になっている。同様に傾斜変動に対する伝達関数は\omega_0をコーナー周波数とする二次バタワース型ローパスフィルタと同じ形である。

参考文献・謝辞

他、内部の参考資料も大いに参考にしました。
また、ChatGPT氏にはいろいろ相談に乗っていただきました。

脚注

  1. 速度に比例する電圧が出力となる電磁式地震計を考えたいため。 ↩︎

  2. 鉛直方向については傾斜応答が水平ほど現れない。下部参考文献中の議論を参照のこと。 ↩︎

  3. \sin(\psi)\simeq \psi が成立する微小な変化を仮定している。通常はせいぜい\mathrm{\mu rad}オーダー程度の話なので十分成り立つ。 ↩︎

Discussion